Lotgerade zu einer Gerade

Die Lotgerade \(\ell\) zu einer Gerade \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\) ist im \(\mathbb R^{3}\) durch die Angabe eines Punktes \(P\) mit den Eigenschaften \(P \in \ell\) und \(P \notin g\) eindeutig festgelegt.

 

Bestimmung der Gleichung der Lotgerade \(\ell\)

 

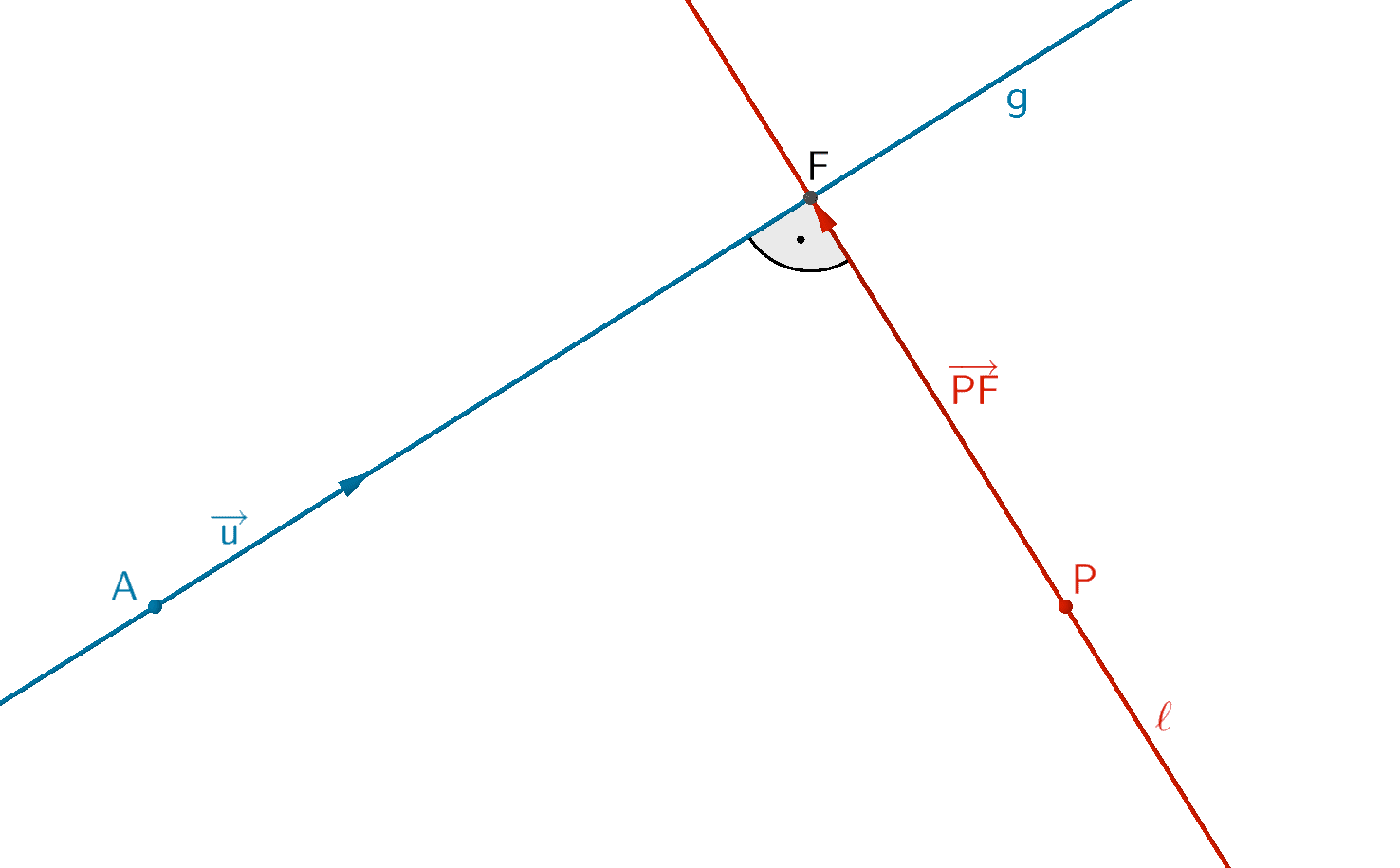
Sei \(F\) der Lotfußpunkt des Lotes des Punktes \(P\) auf die Gerade \(g\), so lässt sich die Gleichung der Lotgerade \(\ell\) durch den Punkt \(P\) zur Gerade \(g\) mithilfe des Aufpunktes \(P\) und dem Richtungsvektor \(\overrightarrow{PF}\) beschreiben.

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

 

Es gibt mehrere Möglichkeiten, den Richtungsvektor \(\overrightarrow{PF}\) der Lotgerade \(\ell\) zu bestimmen.

 

1. Möglichkeit: Skalarprodukt ortogonaler (senkrechter) Vektoren anwenden 

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

 

Der Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) und der Richtungsvektor \(\overrightarrow{PF}\) der Lotgerade \(\ell\) stehen senkrecht zueinander. Folglich ist das Skalarprodukt der Richtungsvektoren gleich Null (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).

 

\[\overrightarrow{u} \perp \overrightarrow{PF} \quad \Longleftrightarrow \quad \overrightarrow{u} \circ \overrightarrow{PF} = 0\]

 

Der Richtungsvektor \(\overrightarrow{PF}\) der Lotgerade \(\ell\) lässt sich in Abhängigkeit des Parameters \(\lambda\) der Gleichung der Gerade \(g\) beschreiben.

 

\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\]

 

\[F \in g \colon \overrightarrow{F} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\]

 

\[\overrightarrow{PF} = \overrightarrow{F} - \overrightarrow{P} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} - \overrightarrow{P}\]

 

Wendet man nun das Skalarprodukt der orthogonalen Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{PF}\) an, liefert dies genau den Wert des Parameters \(\lambda\), der den Richtungsvektor \(\overrightarrow{PF}\) der Gleichung der Lotgerade \(\ell\) festlegt.

 

\[\begin{align*}\overrightarrow{u} \circ \overrightarrow{PF} &= 0 \\[0.8em] \overrightarrow{u} \circ (\overrightarrow{A} + \lambda \cdot \overrightarrow{u} - \overrightarrow{P}) &= 0 \end{align*}\]

 

\(\Longrightarrow \quad\)Parameterwert für \(\lambda\)

\(\Longrightarrow \quad \)Richtungsvektor \(\overrightarrow{PF}\) der Lotgeraden \(\ell\)

\[\Longrightarrow \quad \ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

 

Beispiel:

Gegeben sei die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\) sowie der Punkt \(P(-4|8|2)\), welcher nicht auf der Gerade \(g\) liegt.

Ermitteln Sie eine Gleichung der Lotgerade \(\ell\) durch den Punkt \(P\) zur Gerade \(g\).

 

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]

\[P(-4|8|2)\]

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

 

Richtungsvektor \(\overrightarrow{PF}\) der Lotgerade \(\ell\) in Abhängigkeit des Parameters \(\lambda\) der Gleichung der Gerade \(g\) beschreiben:

 

\[F \in g \colon \overrightarrow{F} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 6 - 3\lambda \\ 3 \\ 2 + \lambda \end{pmatrix}\]

 

\[\overrightarrow{PF} = \overrightarrow{F} - \overrightarrow{P} = \begin{pmatrix} 6 - 3\lambda \\ 3 \\ 2 + \lambda \end{pmatrix} - \begin{pmatrix} -4 \\ 8 \\ 2 \end{pmatrix} = \begin{pmatrix} 10 - 3\lambda \\ -5 \\ \lambda \end{pmatrix}\]

 

Skalarprodukt der ortogonalen Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{PF}\) anwenden:

 

\[\begin{align*}\overrightarrow{u} \circ \overrightarrow{PF} &= 0 \\[0.8em] \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 10 - 3\lambda \\ -5 \\ \lambda \end{pmatrix} &= 0 \\[0.8em] (-3) \cdot (10 - 3\lambda) + 0 \cdot (-5) + 1 \cdot \lambda &= 0 \\[0.8em] -30 + 10\lambda &= 0 & &| + 30 \\[0.8em] 10\lambda &= 30 & &| : 10 \\[0.8em] \lambda &= 3 \end{align*}\]

 

Richtungsvektor \(\overrightarrow{PF}\) der Lotgerade \(\ell\) berechnen:

 

\[\overrightarrow{PF} = \begin{pmatrix} 10 - 3\lambda \\ -5 \\ \lambda \end{pmatrix} = \begin{pmatrix} 10 - 3 \cdot 3 \\ -5 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ -5 \\ 3 \end{pmatrix}\]

 

Gleichung der Lotgerade \(\ell\) formulieren:

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

\[P(-4|8|2)\]

 

\[\ell \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 8 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ -5 \\ 3 \end{pmatrix}; \; \mu \in \mathbb R\]

 

2. Möglichkeit: Hilfsebene aufstellen

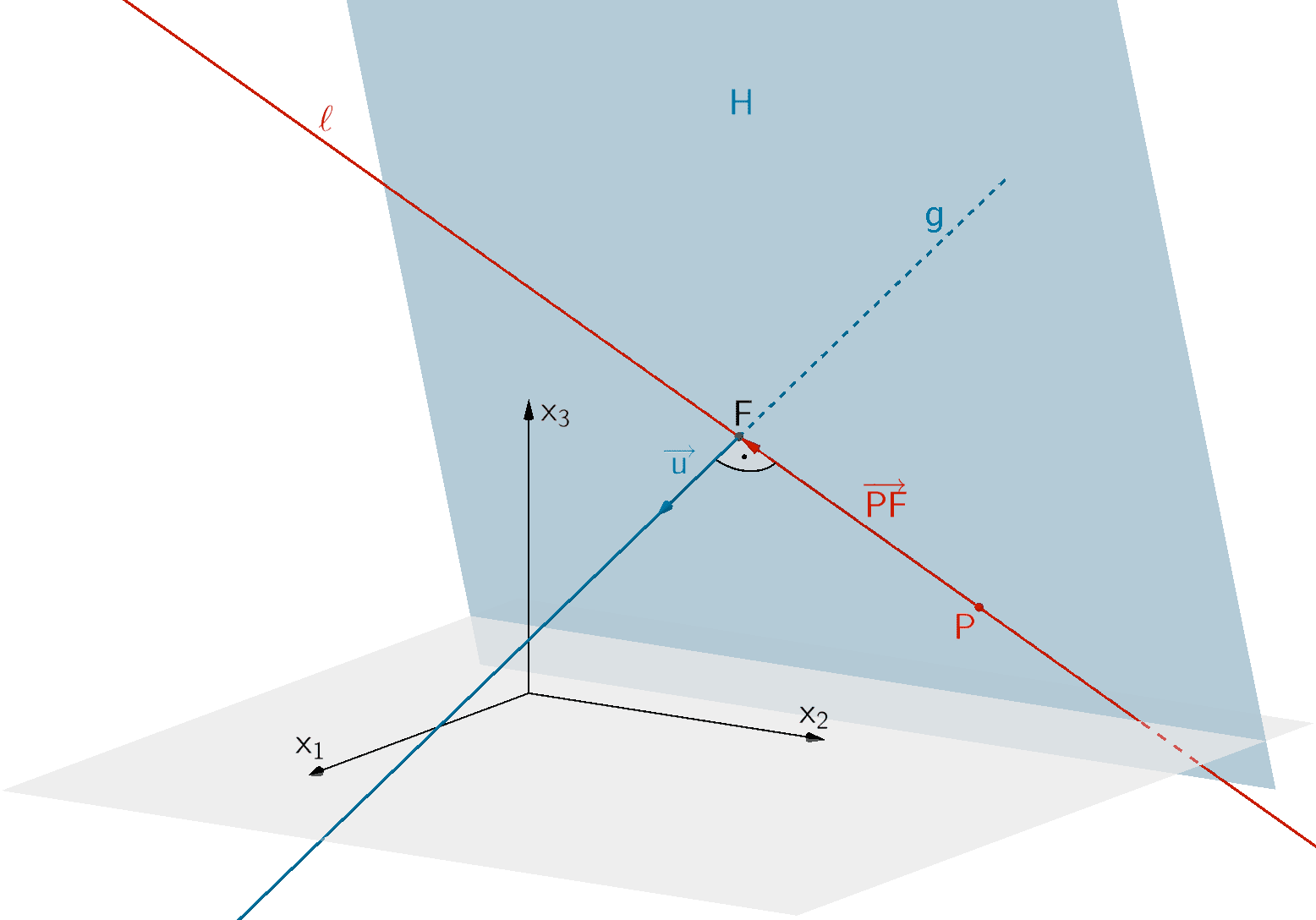
Die Hilfsebene \(H\) mit den Eigenschaften \(P \in H\) und \(g \perp H\) schneidet die Gerade \(g\) im Lotfußpunkt \(F\) des Lotes des Punktes \(P\) auf die Gerade \(g\).

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

 

Um den Richtungsvektor \(\overrightarrow{PF}\) der Gleichung der Lotgerade \(\ell\) zu bestimmen, stellt man eine Hilfsebene \(H\) auf, welche den Punkt \(P\) enthält und senkrecht zur Gerade \(g\) liegt. Als Normalenvektor für die Gleichung der Hilfsebene \(H\) in Normalenform dient der Richtungsvektor \(\overrightarrow{u}\) der Geradengleichung von \(g\).

 

\[P \in H\]

\[g \perp H \quad \Longrightarrow \quad \overrightarrow{n}_{H} = \overrightarrow{u}\]

\[H \colon \overrightarrow{u} \circ (\overrightarrow{X} - \overrightarrow{P}) = 0\]

 

Der Richtungsvektor \(\overrightarrow{PF}\) der Lotgerade \(\ell\) lässt sich in Abhängigkeit des Parameters \(\lambda\) der Gleichung der Gerade \(g\) beschreiben.

 

\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\]

 

\[F \in g \colon \overrightarrow{F} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\]

 

\[\overrightarrow{PF} = \overrightarrow{F} - \overrightarrow{P} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} - \overrightarrow{P}\]

 

Schneidet man die Gerade \(g\) mit der Hilfsebene \(H\), erhält man genau den Wert des Parameters \(\lambda\), der den Richtungsvektor \(\overrightarrow{PF}\) der Gleichung der Lotgerade \(\ell\) festlegt (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene, Bestimmung des Schnittpunkts).

 

\[g \cap H \colon \overrightarrow{u} \circ (\overrightarrow{A} + \lambda \cdot \overrightarrow{u} - \overrightarrow{P}) = 0\]

 

\(\Longrightarrow \quad\)Parameterwert für \(\lambda\)

\(\Longrightarrow \quad \)Richtungsvektor \(\overrightarrow{PF}\) der Lotgeraden \(\ell\)

\[\Longrightarrow \quad \ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

 

Beispiel (vgl. 1. Möglichkeit):

Gegeben sei die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\) sowie der Punkt \(P(-4|8|2)\), welcher nicht auf der Gerade \(g\) liegt.

Ermitteln Sie eine Gleichung der Lotgerade \(\ell\) durch den Punkt \(P\) zur Gerade \(g\).

 

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]

\[P(-4|8|2)\]

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

 

Gleichung der Hilfsebene \(H\) aufstellen:

 

\(P \in H\,, \; g \perp H\)

 

\[H \colon \overrightarrow{u} \circ (\overrightarrow{X} - \overrightarrow{P}) = 0\]

\[H \colon \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} -4 \\ 8 \\ 2 \end{pmatrix} \right] = 0\]

 

\[\begin{align*} \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} -4 \\ 8 \\ 2 \end{pmatrix} \right] &= 0 \\[0.8em] (-3) \cdot (x_{1} + 4) + 0 \cdot (x_{2} - 8) + 1 \cdot (x_{3} - 2) &= 0 \\[0.8em] -3x_{1} - 12 + x_{3} - 2 &= 0 \\[0.8em] -3x_{1} + x_{3} - 14 &= 0 \end{align*}\]

 

\[H \colon -3x_{1} + x_{3} - 14 = 0\]

 

Richtungsvektor \(\overrightarrow{PF}\) der Lotgerade \(\ell\) in Abhängigkeit des Parameters \(\lambda\) der Gleichung der Gerade \(g\) beschreiben:

 

\[F \in g \colon \overrightarrow{F} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 6 - 3\lambda \\ 3 \\ 2 + \lambda \end{pmatrix}\]

 

\[\overrightarrow{PF} = \overrightarrow{F} - \overrightarrow{P} = \begin{pmatrix} 6 - 3\lambda \\ 3 \\ 2 + \lambda \end{pmatrix} - \begin{pmatrix} -4 \\ 8 \\ 2 \end{pmatrix} = \begin{pmatrix} 10 - 3\lambda \\ -5 \\ \lambda \end{pmatrix}\]

 

Gerade \(g\) mit der Hilfsebene \(H\) schneiden (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene, Bestimmung des Schnittpunkts):

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]

\[H \colon -3x_{1} + x_{3} - 14 = 0\]

 

\[\begin{align*} g \cap H \colon (-3) \cdot (6 - 3\lambda) + 2 + \lambda - 14 &= 0 \\[0.8em] -18 + 9\lambda + 2 + \lambda - 14 &= 0 \\[0.8em] -30 + 10\lambda &= 0 & &| + 30 \\[0.8em] 10\lambda &= 30 & &| : 10 \\[0.8em] \lambda &= 3 \end{align*}\]

 

Richtungsvektor \(\overrightarrow{PF}\) der Lotgerade \(\ell\) berechnen:

 

\[\overrightarrow{PF} = \begin{pmatrix} 10 - 3\lambda \\ -5 \\ \lambda \end{pmatrix} = \begin{pmatrix} 10 - 3 \cdot 3 \\ -5 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ -5 \\ 3 \end{pmatrix}\]

 

Gleichung der Lotgerade \(\ell\) formulieren:

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

\[P(-4|8|2)\]

 

\[\ell \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 8 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ -5 \\ 3 \end{pmatrix}; \; \mu \in \mathbb R\]

 

3. Möglichkeit: Differentialrechnung anwenden (Extremwertaufgabe)

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

 

Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(P\) auf die Gerade \(g\).

 

Die Länge der Strecke \([PX]\) zwischen dem Punkt \(P\) und einem beliebigen Punkt \(X \in g\) ist gleich dem Betrag des Verbindungsvektors \(\overrightarrow{PX}\).

 

\[\overline{PX} = \vert \overrightarrow{PX} \vert\]

 

Der Verbindungsvektor \(\overrightarrow{PX}\) lässt sich in Abhängigkeit des Parameters \(\lambda\) der Gleichung der Gerade \(g\) beschreiben.

 

\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\]

 

\[\overrightarrow{PX} = \overrightarrow{X} - \overrightarrow{P} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} - \overrightarrow{P}\]

 

Für \(X = F\) ist die Länge der Strecke \(\overline{PX}\) minimal. Folglich muss die erste Ableitung \(\overline{PX}'\) gleich Null sein (vgl. 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte und Abiturskript - 1.5.7 Extremwertaufgaben). Der Nachweis der Art des Extremwerts kann entfallen, denn für \(X \neq F\) nimmt die Länge der Strecke \([PX]\) einen beliebig großen Wert an. Somit existiert keine maximale Länge der Strecke \([PX]\).

Die Extremstelle \(\lambda_{min}\) liefert genau den Wert des Parameters \(\lambda\), der den Richtungsvektor \(\overrightarrow{PF}\) der Gleichung der Lotgerade \(\ell\) festlegt.

 

\[\overline{PX}'(\lambda) \overset{!}{=} 0\]

 

\(\Longrightarrow \quad\)Parameterwert für \(\lambda\)

\(\Longrightarrow \quad \)Richtungsvektor \(\overrightarrow{PF}\) der Lotgeraden \(\ell\)

\[\Longrightarrow \quad \ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

 

Beispiel (vgl. 1. und 2. Möglichkeit):

Gegeben sei die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\) sowie der Punkt \(P(-4|8|2)\), welcher nicht auf der Gerade \(g\) liegt.

Ermitteln Sie eine Gleichung der Lotgerade \(\ell\) durch den Punkt \(P\) zur Gerade \(g\).

 

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix}  + \lambda \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]

\[P(-4|8|2)\]

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

 

Verbindungsvektor \(\overrightarrow{PX}\) in Abhängigkeit des Parameters \(\lambda\) der Gleichung der Gerade \(g\) beschreiben:

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 3 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 6 - 3\lambda \\ 3 \\ 2 + \lambda \end{pmatrix}\]

 

\[\overrightarrow{PX} = \overrightarrow{X} - \overrightarrow{P} = \begin{pmatrix} 6 - 3\lambda \\ 3 \\ 2 + \lambda \end{pmatrix} - \begin{pmatrix} -4 \\ 8 \\ 2 \end{pmatrix} = \begin{pmatrix} 10 - 3\lambda \\ -5 \\ \lambda \end{pmatrix}\]

 

Länge der Strecke \([PX]\) in Abhängigkeit des Parameters \(\lambda\) formulieren:

 

\[\begin{align*} \overline{PX} &= \vert \overrightarrow{PX} \vert \\[0.8em] &= \left| \begin{pmatrix} 10 - 3\lambda \\ -5 \\ \lambda \end{pmatrix} \right| \\[0.8em] &= \sqrt{(10 - 3\lambda)^{2} + (-5)^{2} + \lambda^{2}} \\[0.8em] &= \sqrt{100 - 60\lambda + 9\lambda^{2} + 25 + \lambda^{2}} \\[0.8em] &= \sqrt{10\lambda^{2} - 60\lambda + 125} \end{align*}\]

 

Notwendige Bedingung \(\overline{PX}'(\lambda) = 0\) für minimale Länge der Strecke \([PX]\) (vgl. Abiturskript - 1.5.2 Ableitungsregeln):

 

\[\begin{align*} \overline{PX}'(\lambda) &= 0 \\[0.8em] \left( \sqrt{10\lambda^{2} - 60\lambda + 125} \right)' &= 0 \\[0.8em] \frac{20\lambda - 60}{2 \cdot \sqrt{10\lambda^{2} - 60\lambda + 125}} &= 0 \end{align*}\]

 

\[\begin{align*}\Longrightarrow \quad 20\lambda - 60 &= 0 & &| + 60 \\[0.8em] 20\lambda &= 60 & &| : 20 \\[0.8em] \lambda &= 3\end{align*}\]

 

Richtungsvektor \(\overrightarrow{PF}\) der Lotgeraden \(\ell\) berechnen:

 

\[\overrightarrow{PF} = \begin{pmatrix} 10 - 3\lambda \\ -5 \\ \lambda \end{pmatrix} = \begin{pmatrix} 10 - 3 \cdot 3 \\ -5 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ -5 \\ 3 \end{pmatrix}\]

 

Gleichung der Lotgerade \(\ell\) formulieren:

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \mu \cdot \overrightarrow{PF}\,; \; \mu \in \mathbb R\]

\[P(-4|8|2)\]

 

\[\ell \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ 8 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ -5 \\ 3 \end{pmatrix}; \; \mu \in \mathbb R\]

Lotgerade zu zwei windschiefen Geraden

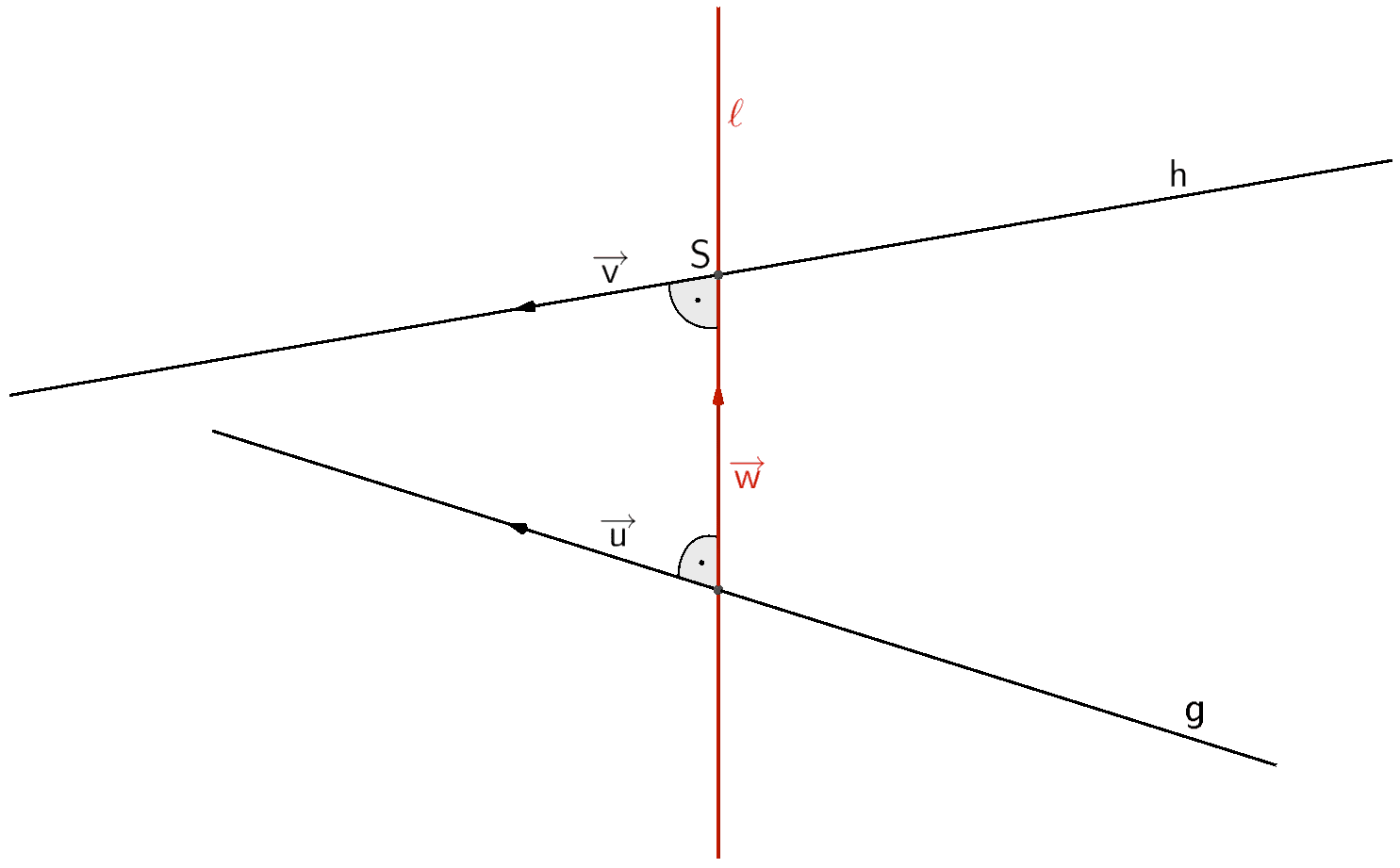
Diie Lotgerade \(\ell\) zu zwei windschiefen Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\,; \; \mu \in \mathbb R\) wird festgelegt durch einen Richtungsvektor \(\overrightarrow{w}\), der sowohl zum Richtungsvektor \(\overrightarrow{u}\) der Geraden \(g\) als auch zum Richtungsvektor \(\overrightarrow{v}\) der Gerade \(h\) senkrecht ist, und einen Schnittpunkt \(S\) der Lotgerade \(\ell\) mit der Gerade \(g\) oder mit der Gerade \(h\).

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{S} + \tau \cdot \overrightarrow{w}\,; \; \tau \in \mathbb R\]

 

Richtungsvektor der Lotgerade \(\ell\)

Ein Richtungsvektor \(\overrightarrow{w}\) der Lotgerade \(\ell\) lässt sich mithilfe des Vektorprodukts der Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) der windschiefen Geraden \(g\) und \(h\) bestimmen (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\overrightarrow{w} = \overrightarrow{u} \times \overrightarrow{v}\]

 

Jedes Vielfache des Vektorprodukts \(\overrightarrow{u} \times \overrightarrow{v}\) ist ebenfalls ein Richtungsvektor \(\overrightarrow{w}\) der Lotgerade \(\ell\).

 

Aufpunkt der Lotgerade \(\ell\)

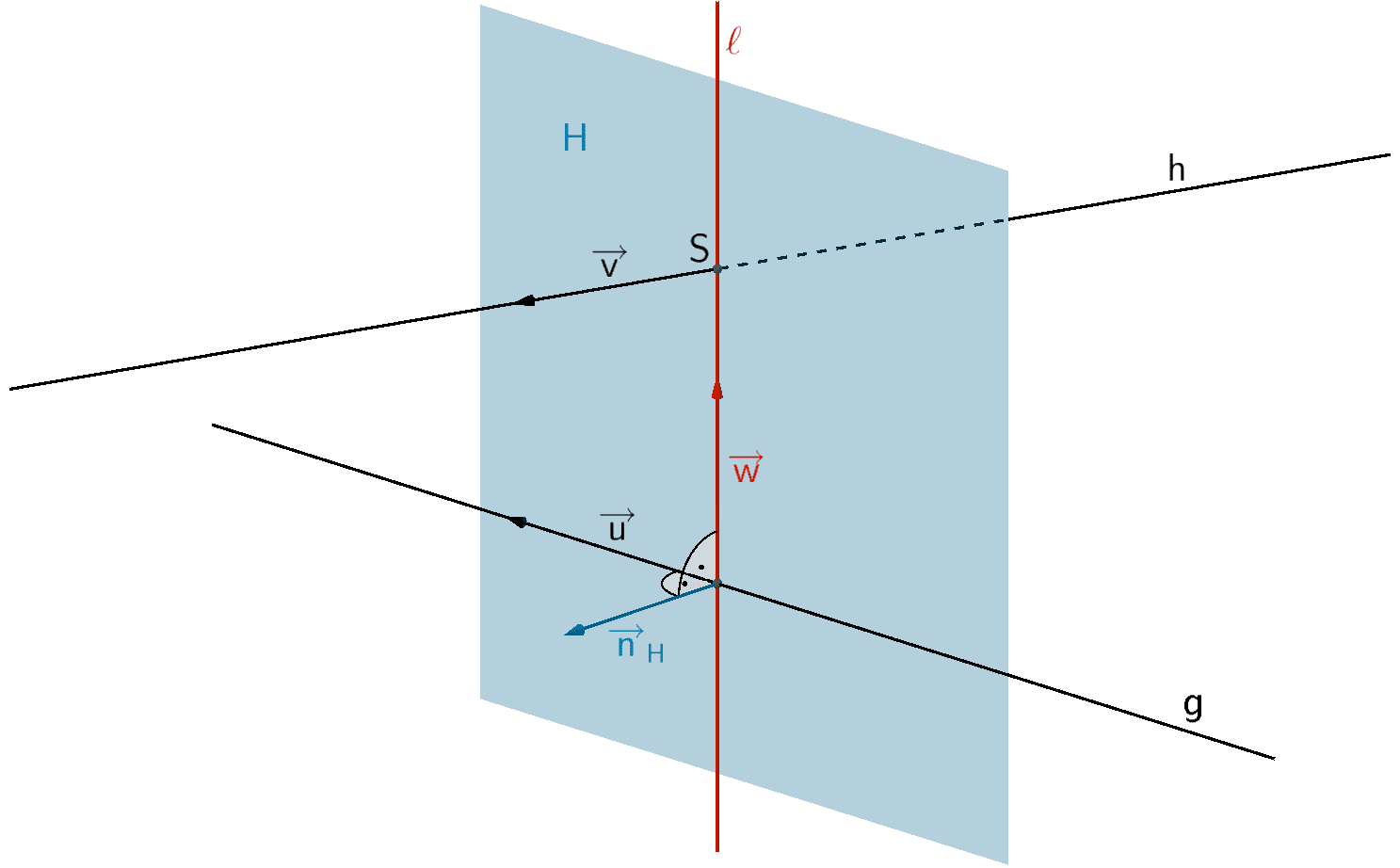
Als Aufpunkt für die Gleichung der Lotgerade \(\ell\) dient einer der beiden Schnittpunkte der Lotgerade mit einer der windschiefen Geraden, beispielsweise der Schnittpunkt \(S\) der Lotgerade \(\ell\) mit der Gerade \(h\).

Für die Bestimmung des Schnittpunkts \(S\) stellt man die Gleichung einer Hilfsebene \(H\) auf, welche die Gerade \(g\) und die Lotgerade \(\ell\) enthält. Man erhält den Normalenvektor \(\overrightarrow{n}_{H}\) der Hilfsebene \(H\) mithilfe des Vektorprodukts aus dem Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) und dem Richtungsvektor \(\overrightarrow{w}\) der Lotgerade \(\ell\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\overrightarrow{n}_{H} = \overrightarrow{u} \times \overrightarrow{w}\]

 

Jedes Vielfache des Vektorprodukts \(\overrightarrow{u} \times \overrightarrow{w}\) ist ebenfalls ein Normalenvektor \(\overrightarrow{n}_{H}\) der Hilfsebene \(H\).

 

Als Aufpunkt für die Gleichung der Hilfsebene \(H\) in Normalenform kommt jeder Punkt der Gerade \(g\) in Frage. Man wählt zweckmäßig den bekannten Aufpunkt \(A\) der Gerade \(g\).

 

\[H \colon \overrightarrow{n}_{H} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

 

Schneidet man die Gerade \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\,; \; \mu \in \mathbb R\) und die Hilfsebene \(H\), erhält man genau den Wert des Parameters \(\mu\), der den Ortsvektor des Schnittpunkts \(S\) der Gerade \(h\) und der Lotgerade \(\ell\) festlegt (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene, Bestimmung des Schnittpunkts).

 

\[h \cap H \colon \overrightarrow{n}_{H} \circ (\overrightarrow{B} + \mu \cdot \overrightarrow{v} - \overrightarrow{A}) = 0\]

 

\(\Longrightarrow \quad\)Parameterwert für \(\mu\)

\(\Longrightarrow \quad\)Schnittpunkt \(S\) der Geraden \(h\) und der Lotgeraden \(\ell\)

\[\Longrightarrow \quad \ell \colon \overrightarrow{X} = \overrightarrow{S} + \tau \cdot \overrightarrow{w}\,; \; \tau \in \mathbb R\]

 

Beispiel:

Gegeben seien die windschiefen Geraden \(g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}; \; \mu \in \mathbb R\).

Bestimmen Sie eine Gleichung der Lotgerade \(\ell\) zu den Geraden \(g\) und \(h\).

 

 

Es gilt: \(\ell \perp g\), \(\ell \perp h\)

Es sei der Schnittpunkt \(S\) der Gerade \(h\) und der Lotgerade \(\ell\) der Aufpunkt der Lotgerade \(\ell\) und \(\overrightarrow{w}\) der Richtungsvektor der Lotgerade \(\ell\).

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{S} + \tau \cdot \overrightarrow{w}\,; \; \tau \in \mathbb R\]

 

Richtungsvektor \(\overrightarrow{w}\) der Lotgerade \(\ell\)

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R \quad \Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\]

\[h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}; \; \mu \in \mathbb R \quad \Longrightarrow \quad \overrightarrow{v} = \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}\]

 

\[\overrightarrow{w} = \overrightarrow{u} \times \overrightarrow{v} \quad \Longrightarrow \quad \overrightarrow{w} \perp \overrightarrow{u}, \; \overrightarrow{w} \perp \overrightarrow{v}\]

 

\[\begin{align*} \overrightarrow{u} \times \overrightarrow{v} &= \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \times \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 1 & \cdot & 0 & - & 0 & \cdot & 1 \\ 0 & \cdot & (-3) & - & 0 & \cdot & 0 \\ 0 & \cdot & 1 & - & 1 & \cdot & (-3) \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} \\[0.8em] &= 3 \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \end{align*}\]

 

\[\Longrightarrow \quad \overrightarrow{w} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]

 

Aufpunkt \(S\) der Lotgerade \(\ell\)

Der Schnittpunkt \(S\) der Gerade \(h\) und der Lotgerade \(\ell\) dient als Aufpunkt der Lotgerade \(\ell\). Die Hilfsebene \(H\) enthält die Gerade \(g\) und die Lotgerade \(\ell\). Sie schneidet die Gerade \(h\) im Schnittpunkt \(S\). Das Vektorprodukt \(\overrightarrow{u} \times \overrightarrow{w}\) liefert einen Normalenvektor \(\overrightarrow{n}_{H}\) der Hilfsebene \(H\).

 

\[g \subset H, \, \ell \subset H \quad \Longrightarrow \quad \overrightarrow{n}_{H} = \overrightarrow{u} \times \overrightarrow{w}\]

\[\overrightarrow{u} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \overrightarrow{w} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]

 

\[\begin{align*}\overrightarrow{n}_{H} &= \overrightarrow{u} \times \overrightarrow{w} \\[0.8em] &= \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 1 & \cdot & 1 & - & 0 & \cdot & 0 \\ 0 & \cdot & 0 & - & 0 & \cdot & 1 \\ 0 & \cdot & 0 & - & 1 & \cdot & 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \end{align*}\]

 

Als Aufpunkt für die Hilfsebene \(H\) kann der Aufpunkt der Gerade \(g\) verwendet werden.

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R \quad \Longrightarrow \quad (2|-6|2) \in g\]

 

\[\Longrightarrow \quad H \colon \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} \right] = 0\]

 

\[\begin{align*} \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} \right] &= 0 \\[0.8em] 1 \cdot (x_{1} - 2) + 0 \cdot (x_{2} + 6) + 0 \cdot (x_{3} - 2) &= 0 \\[0.8em] x_{1} - 2 &= 0 \end{align*}\]

 

\[\Longrightarrow \quad H \colon x_{1} - 2 = 0\]

 

Gerade \(h\) mit der Hilfsebene \(H\) schneiden und die Koordinaten des Schnittpunkts \(S\) berechnen (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene, Bestimmung des Schnittpunkts):

 

\[h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}; \; \mu \in \mathbb R\]

\[H \colon x_{1} - 2 = 0\]

 

\[\begin{align*} h \cap H \colon 6 - 3\mu - 2 &= 0 \\[0.8em] 4 - 3 \mu &= 0 & &| + 3\mu \\[0.8em] 4 &= 3\mu & &| : 3 \\[0.8em] \frac{4}{3} &= \mu \end{align*}\]

 

\[\overrightarrow{S} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \frac{4}{3} \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ -\frac{2}{3} \\ 8 \end{pmatrix}\]

 

Gleichung der Lotgerade \(\ell\) formulieren:

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{S} + \tau \cdot \overrightarrow{w}\,; \; \tau \in \mathbb R\]

 

\[\overrightarrow{S} = \begin{pmatrix} 2 \\ -\frac{2}{3} \\ 8 \end{pmatrix}; \; \overrightarrow{w} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]

 

\[\Longrightarrow \quad \ell \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -\frac{2}{3} \\ 8 \end{pmatrix} + \tau \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}; \; \tau \in \mathbb R\]

Lotgerade zu einer Ebene

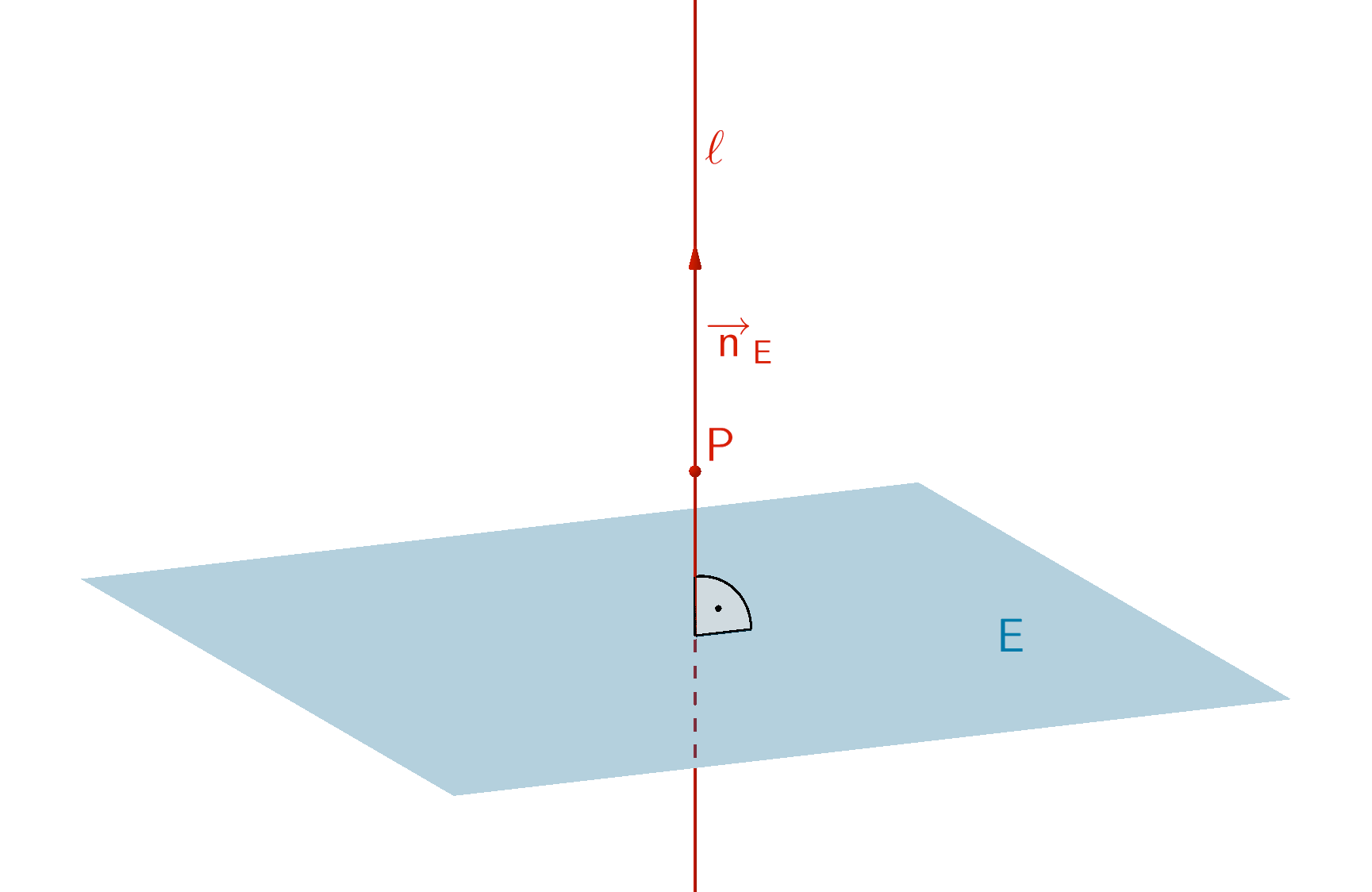
Eine Lotgerade \(\ell\) zu einer Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) ist durch einen beliebigen Punkt \(P \in \ell\) und den Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) eindeutig festgelegt.

 

\[\ell \colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_{E}\,; \; \lambda \in \mathbb R\]

 

Jedes Vielfache des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\) ist ebenfalls ein Richtungsvektor der Lotgerade \(\ell\).

 

Beispiel:

Geben sei die Ebene \(E \colon 2x_{1} - 3x_{2} + 4x_{3} - 3 = 0\).

Geben Sie eine Gleichung der Lotgerade \(\ell\) zur Ebene \(E\) an, welche durch den Punkt \(P(-1|5|-3)\) verläuft.

 

\[E \colon 2x_{1} - 3x_{2} + 4x_{3} - 3 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}\]

\[P(-1|5|-3)\]

 

\[\Longrightarrow \quad \ell \colon \overrightarrow{X} = \begin{pmatrix} -1 \\ 5 \\ -3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}; \; \lambda \in \mathbb R\]

Orthogonale Ebene zu einer Gerade

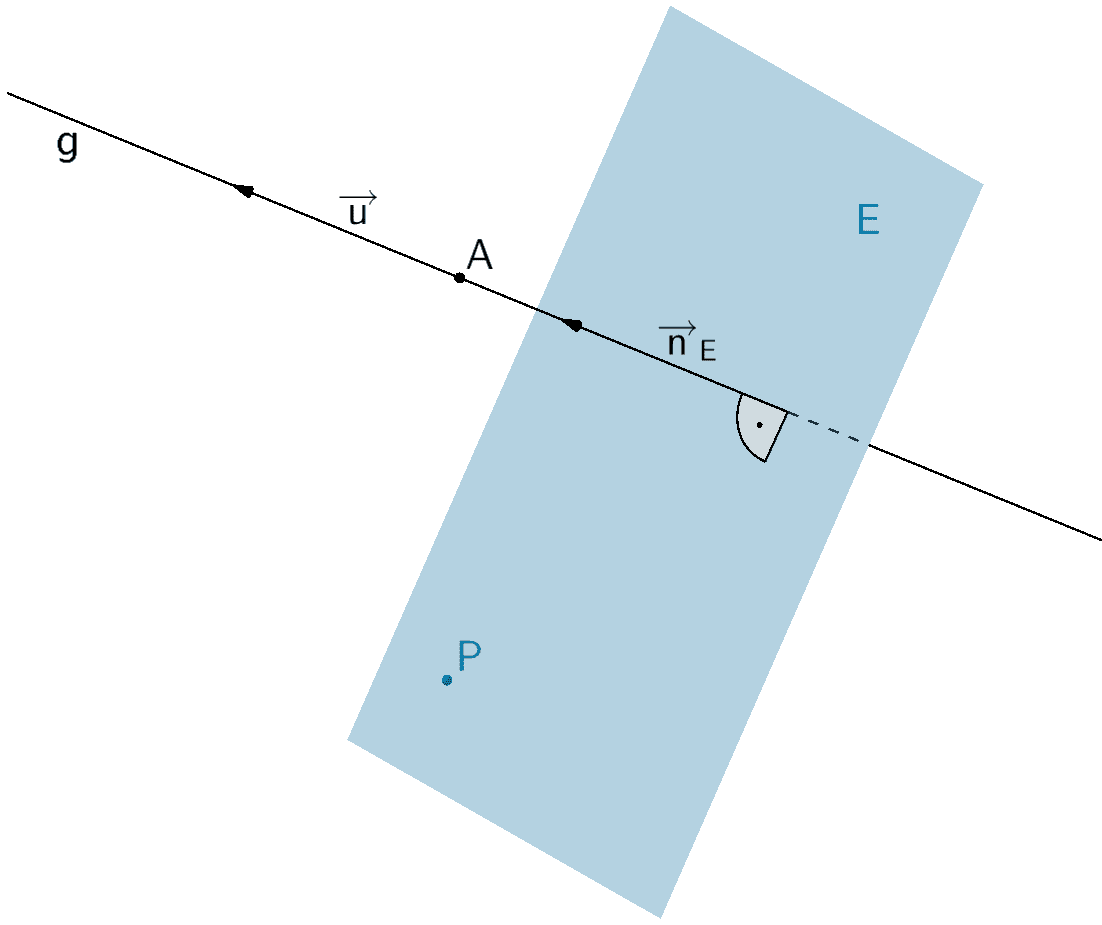
Eine orthogonale (senkrechte) Ebene \(E\) zu einer Gerade \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) ist durch einen beliebigen Punkt \(P \in E\) und den Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) eindeutig festgelegt.

 

\[E \colon \overrightarrow{u} \circ (\overrightarrow{X} - \overrightarrow{P})\]

 

Jedes Vielfache des Richtungsvektors \(\overrightarrow{u}\) der Gerade \(g\) ist ebenfalls ein Normalenvektor der Ebene \(E\).

 

Beispiel:

Gegeben sei die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} -1 \\ 4 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R\).

Geben Sie die Gleichung einer Ebene \(E\) an, welche den Punkt \(P(0|-4|3)\) enthält und senkrecht zur Gerade \(g\) ist.

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} -1 \\ 4 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R \quad \Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix}\]

\[P(0|-4|3)\]

 

\[\Longrightarrow \quad E \colon \begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix} \right] = 0\]

Orthogonale Ebene zu einer Ebene

Nachfolgend werden zwei Fälle behandelt, welche eine orthogonale (senkrechte) Ebene \(F\) zu einer Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) festlegen. Zudem wird ein Fall einer zu zwei nicht parallelen Ebenen \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) und \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B})\) orthogonalen Ebene \(G\) vorgestellt.

 

Orthogonale Ebene \(F\) durch zwei Punkte \(P\) und \(Q\) zu einer Ebene \(E\)

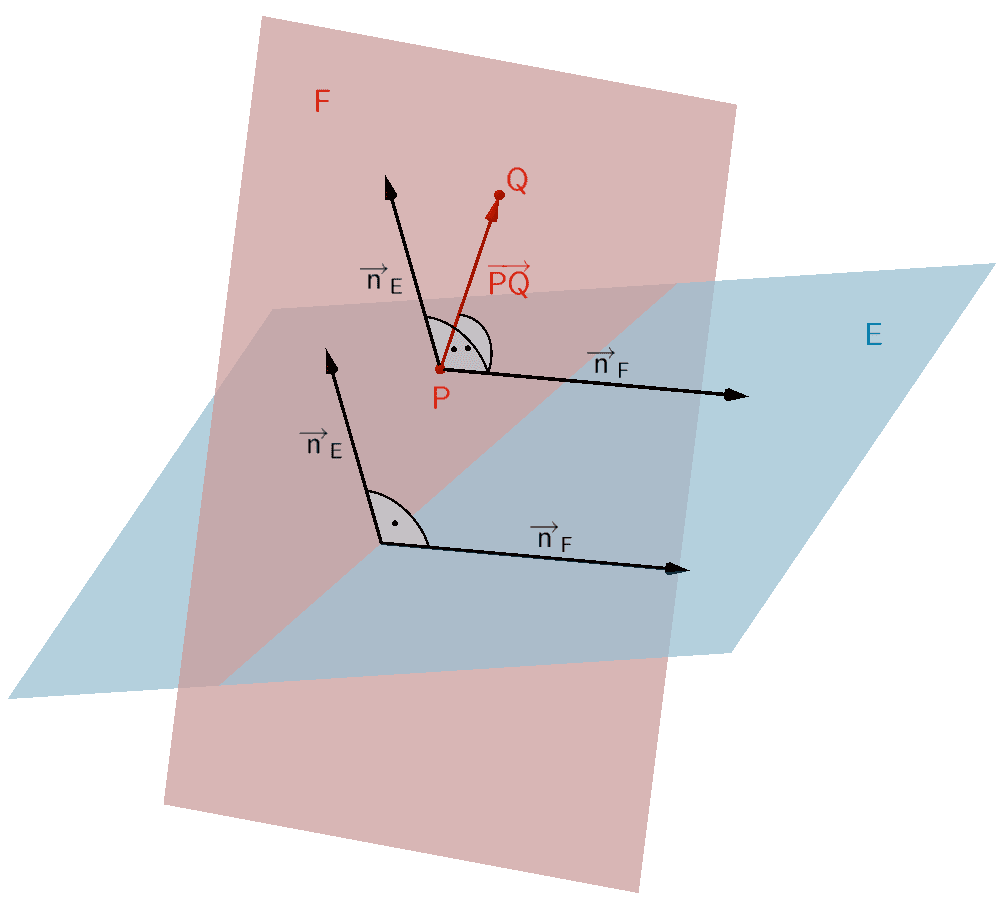
Eine orthogonale Ebene \(F\) zu einer Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) ist durch zwei Punkte \(P \in F\) und \(Q \in F\) \((P \neq Q)\) eindeutig festgelegt, wenn der Verbindungsvektor \(\overrightarrow{PQ}\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) linear unabhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren). Die Punkte \(P\) und \(Q\) dürfen also nicht auf einer Lotgerade zur Ebene \(E\) liegen.

 

\[\overrightarrow{PQ} \neq k \cdot \overrightarrow{n}_{E}; \; k \in \mathbb R\]

 

Der Normalenvektor \(\overrightarrow{n}_{F}\) der orthogonalen Ebene \(F\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenen \(E\) und dem Verbindungsvektor \(\overrightarrow{PQ}\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\overrightarrow{n}_{F} = \overrightarrow{n}_{E} \times \overrightarrow{PQ}\]

 

Jedes Vielfache des Vektorprodukts \(\overrightarrow{n}_{E} \times \overrightarrow{PQ}\) ist ebenfalls ein Normalenvektor der Ebene \(F\).

 

Als Aufpunkt der orthogonalen Ebene \(F\) wählt man einen der Punkte \(P\) oder \(Q\).

 

\(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{P}) = 0\) oder \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{Q})\)

 

Beispiel:

Gegeben seien die Ebene \(E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\) sowie die Punkte \(P(0|0{,}5|3)\) und \(Q(-1|0|6)\).

Ermitteln Sie eine Gleichung der Ebene \(F\), welche die Punkte \(P\) und \(Q\) enthält und zur Ebene \(E\) senkrecht ist.

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\]

\(P(0|0{,}5|3)\), \(Q(-1|0|6)\)

\(P, Q \in F\), \(F \perp E\)

 

Überprüfen, ob die Punkte \(P\) und \(Q\) eine Ebene \(F \perp E\) festlegen:

Die Punkte \(P\) und \(Q\) legen eine Ebene \(F \perp E\) fest, wenn der Verbindungsvektor \(\overrightarrow{PQ}\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) linear unabhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren).

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}\]

 

\[\overrightarrow{PQ} = \overrightarrow{Q} - \overrightarrow{P} = \begin{pmatrix} -1 \\ 0 \\ 6 \end{pmatrix} - \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} = \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}\]

 

\[\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \neq k \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}; \: k \in \mathbb R\]

 

\(\Longrightarrow \quad\)\(\overrightarrow{PQ}\) und \(\overrightarrow{n}_{E}\) sind linear unabhängig.

\(\Longrightarrow \quad\)Die Punkte \(P\) und \(Q\) legen eine Ebene \(F \perp E\) fest.

 

Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) berechnen:

Der Normalenvektor \(\overrightarrow{n}_{F}\) der orthogonalen Ebene \(F\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenen \(E\) und dem Verbindungsvektor \(\overrightarrow{PQ}\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\begin{align*} \overrightarrow{n}_{E} \times \overrightarrow{PQ} &= \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \times \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 & \cdot & 3 & - & 3 & \cdot & (-0{,}5) \\ 3 & \cdot & (-1) & - & 1 & \cdot & 3 \\ 1 & \cdot & (-0{,}5) & - & 2 & \cdot & (-1) \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 7{,}5 \\ -6 \\ 1{,}5 \end{pmatrix} \\[0.8em] &= 1{,}5 \cdot \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \end{align*}\]

 

\[\Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

Gleichung der Ebene \(F\) formulieren:

Als Aufpunkt der Gleichung der Ebene \(F\) in Normalenform in Vektordarstellung dient der Punkt \(P\) oder der Punkt \(Q\).

 

\(P(0|0{,}5|3)\), \(Q(-1|0|6)\), \(\overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\)

 

\[F \colon \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} \right] = 0\]

oder

\[F \colon\begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} -1 \\ 0 \\ 6 \end{pmatrix} \right] = 0\]

 

\(F \perp E\) überprüfen (Probe):

Mithilfe des Skalarprodukts senkrechter Vektoren überprüft man die Aussage \(F \perp E\) (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).

 

\[\overrightarrow{n}_{F} \circ \overrightarrow{n}_{E} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{F} \perp \overrightarrow{E}, \; F \perp E\]

 

\[\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}; \;\overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

\[\begin{pmatrix}  5 \\ -4 \\ 1\end{pmatrix} \circ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = 5 \cdot 1 + (-4) \cdot 2 + 1 \cdot 3 = 0\]

 

\[\Longrightarrow \quad F \perp E\]

 

Orthogonale Ebene \(F\), welche eine Gerade \(g\) enthält, zu einer Ebene \(E\)

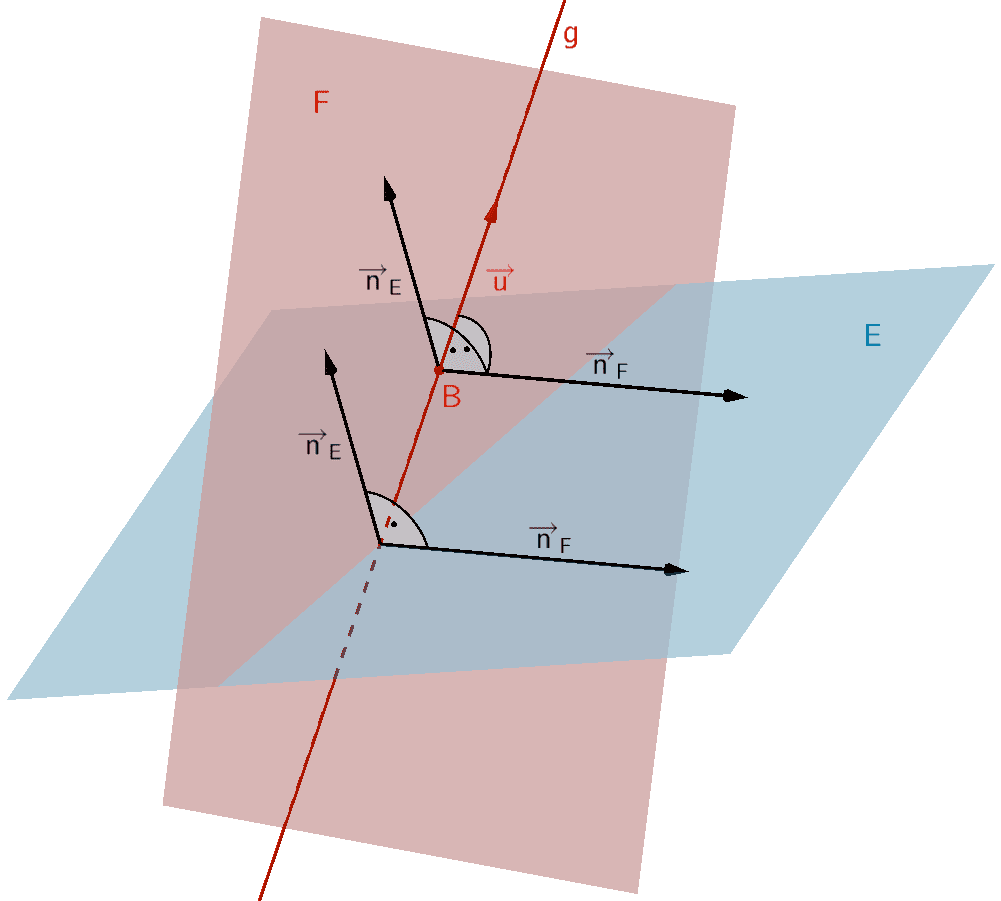
Eine orthogonale Ebene \(F\) zu einer Ebene \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) ist durch eine Gerade \(g \colon \overrightarrow{X} = \overrightarrow{B} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) mit \(g \subset F\) eindeutig festgelegt, wenn der Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) linear unabhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren). Die Gerade \(g\) darf also keine Lotgerade zur Ebene \(E\) sein.

 

\[\overrightarrow{u} \neq k \cdot \overrightarrow{n}_{E}; \; k \in \mathbb R\]

 

Der Normalenvektor \(\overrightarrow{n}_{F}\) der orthogonalen Ebene \(F\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenen \(E\) und dem Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\overrightarrow{n}_{F} = \overrightarrow{n}_{E} \times \overrightarrow{u}\]

 

Jedes Vielfache des Vektorprodukts \(\overrightarrow{n}_{E} \times \overrightarrow{u}\) ist ebenfalls ein Normalenvektor der Ebene \(F\).

 

Als Aufpunkt der orthogonalen Ebene \(F\) wählt man zweckmäßig den Aufpunkt \(B\) der Gerade \(g\).

 

\[F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B}) = 0\]

 

Beispiel:

Gegeben seien die Ebene \(E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\) sowie die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}\,; \; \lambda \in \mathbb R\).

Ermitteln Sie eine Gleichung der Ebene \(F\), welche die Gerade \(g\) enthält und zur Ebene \(E\) senkrecht ist.

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\]

\[g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}\,; \; \lambda \in \mathbb R\]

\(g \subset F\), \(F \perp E\)

 

Überprüfen, ob die Gerade \(g\) eine Ebene \(F \perp E\) festlegt:

Die Gerade \(g\) legt eine Ebene \(F \perp E\) fest, wenn der Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) und der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) linear unabhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren).

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}\]

\[g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix} \quad \Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}\]

 

\[\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \neq k \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix}; \: k \in \mathbb R\]

 

\(\Longrightarrow \quad\)\(\overrightarrow{u}\) und \(\overrightarrow{n}_{E}\) sind linear unabhängig.

\(\Longrightarrow \quad\)Die Gerade \(g\) legt eine Ebene \(F \perp E\) fest.

 

Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) berechnen:

Der Normalenvektor \(\overrightarrow{n}_{F}\) der orthogonalen Ebene \(F\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenen \(E\) und dem Richtungsvektor \(\overrightarrow{u}\) der Geraden \(g\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\begin{align*} \overrightarrow{n}_{E} \times \overrightarrow{u} &= \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \times \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 & \cdot & 3 & - & 3 & \cdot & (-0{,}5) \\ 3 & \cdot & (-1) & - & 1 & \cdot & 3 \\ 1 & \cdot & (-0{,}5) & - & 2 & \cdot & (-1) \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 7{,}5 \\ -6 \\ 1{,}5 \end{pmatrix} \\[0.8em] &= 1{,}5 \cdot \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \end{align*}\]

 

\[\Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

Gleichung der Ebene \(F\) formulieren:

Als Aufpunkt der Gleichung der Ebene \(F\) in Normalenform in Vektordarstellung dient der Aufpunkt der Geradengleichung von \(g\).

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ -0{,}5 \\ 3 \end{pmatrix} \quad \Longrightarrow \quad (0|0{,}5|3) \in g\]

\(\overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\)

 

\[F \colon \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} \right] = 0\]

 

\(F \perp E\) überprüfen (Probe):

Mithilfe des Skalarprodukts senkrechter Vektoren überprüft man die Aussage \(F \perp E\) (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).

 

\[\overrightarrow{n}_{F} \circ \overrightarrow{n}_{E} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{F} \perp \overrightarrow{E}, \; F \perp E\]

 

\[\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}; \;\overrightarrow{n}_{F} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

\[\begin{pmatrix}  5 \\ -4 \\ 1\end{pmatrix} \circ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = 5 \cdot 1 + (-4) \cdot 2 + 1 \cdot 3 = 0\]

 

\[\Longrightarrow \quad F \perp E\]

 

Orthogonale Ebene \(G\) durch einen Punkt \(P\) zu zwei Ebenen \(E\) und \(F\)

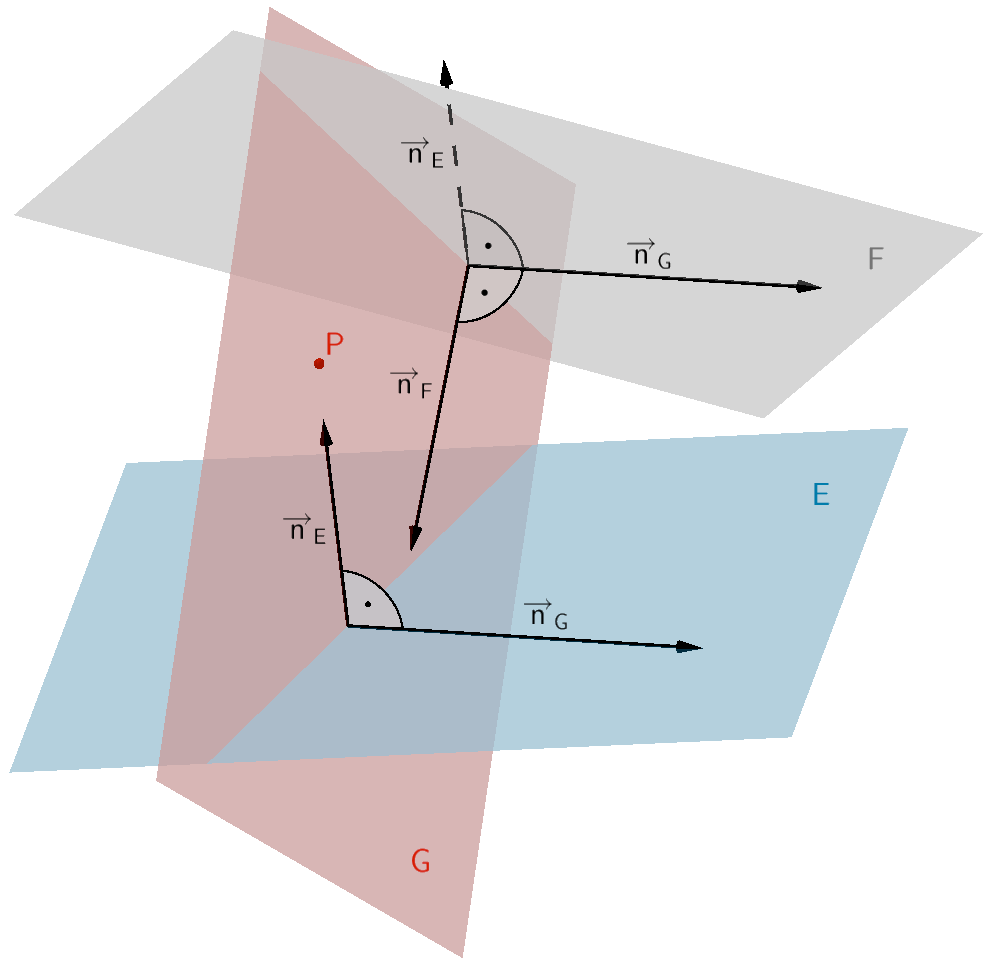
Eine orthogonale Ebene \(G\) zu zwei nicht parallelen Ebenen \(E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A})\) und \(F \colon \overrightarrow{n}_{F} \circ (\overrightarrow{X} - \overrightarrow{B})\) ist durch einen Punkte \(P \in G\) eindeutig festgelegt.

 

\[E \nparallel F \quad \Longrightarrow \quad \overrightarrow{n}_{E} \neq k \cdot \overrightarrow{n}_{F}; \; k \in \mathbb R\]

 

Der Normalenvektor \(\overrightarrow{n}_{G}\) der orthogonalen Ebene \(G\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebenen \(E\) und dem Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\overrightarrow{n}_{G} = \overrightarrow{n}_{E} \times \overrightarrow{n}_{F}\]

 

Jedes Vielfache des Vektorprodukts \(\overrightarrow{n}_{E} \times \overrightarrow{n}_{F}\) ist ebenfalls ein Normalenvektor der Ebene \(G\).

 

Als Aufpunkt der orthogonalen Ebene \(G\) wählt man zweckmäßig Punkt \(P\).

 

\(G \colon \overrightarrow{n}_{G} \circ (\overrightarrow{X} - \overrightarrow{P}) = 0\)

 

Beispiel:

Gegeben seien die Ebene \(E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\) und die Ebene \(F \colon x_{1} - 5x_{3} - 35 = 0\) sowie der Punkt \(P(0|0{,}5|3)\).

Ermitteln Sie eine Gleichung der Ebene \(G\), welche den Punkte \(P\) enthält und zu den Ebenen \(E\) und \(F\) senkrecht ist.

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0\]

\[F \colon x_{1} - 5x_{3} - 35 = 0\]

\[P(0|0{,}5|3)\]

\(P \in G\), \(G \perp E\), \(G \perp F\)

 

Überprüfen, ob die Ebenen \(E\) und \(F\) sowie der Punkt \(P\) eine Ebene \(G \perp E, \,G \perp F\) festlegen:

Die Ebenen \(E\) und \(F\) sowie der Punkt \(P\) legen eine Ebene \(G \perp E, \,G \perp F\) fest, wenn der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) und der Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) linear unabhängig sind (vgl. Abiturskript - 2.1.2 Lineare (Un-)Abhängigkeit von Vektoren).

 

\[E \colon x_{1} + 2x_{2} + 3x_{3} - 3 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}\]

\[F \colon x_{1} - 5x_{3} - 35 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} 1 \\ 0 \\ -5 \end{pmatrix}\]

 

\[\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \neq k \cdot \begin{pmatrix} 1 \\ 0 \\ -5 \end{pmatrix}; \: k \in \mathbb R\]

 

\(\Longrightarrow \quad\)\(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) sind linear unabhängig \((E \nparallel F)\).

\(\Longrightarrow \quad\)Die Ebenen \(E\) und \(F\) sowie der Punkt \(P\) legen eine Ebene \(G \perp E, \,G \perp F\) fest.

 

Normalenvektor \(\overrightarrow{n}_{G}\) der Ebene \(G\) berechnen:

Der Normalenvektor \(\overrightarrow{n}_{G}\) der orthogonalen Ebene \(G\) ergibt sich mithilfe des Vektorprodukts aus dem Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) und dem Normalenvektor \(\overrightarrow{n}_{F}\) der Ebene \(F\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).

 

\[\begin{align*} \overrightarrow{n}_{E} \times \overrightarrow{n}_{F} &= \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \times \begin{pmatrix} 1 \\ 0 \\ -5 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 & \cdot & (-5) & - & 3 & \cdot & 0 \\ 3 & \cdot & 1 & - & 1 & \cdot & (-5) \\ 1 & \cdot & 0 & - & 1 & \cdot & 2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -10 \\ 8 \\ -2 \end{pmatrix} \\[0.8em] &= (-2) \cdot \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \end{align*}\]

 

\[\Longrightarrow \quad \overrightarrow{n}_{G} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

Gleichung der Ebene \(G\) formulieren:

Als Aufpunkt der Gleichung der Ebene \(G\) in Normalenform in Vektordarstellung dient der Punkt \(P\).

 

\(P(0|0{,}5|3)\), \(\overrightarrow{n}_{G} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\)

 

\[G \colon \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 0 \\ 0{,}5 \\ 3 \end{pmatrix} \right] = 0\]

 

\(G \perp E, \, G \perp F\) überprüfen (Probe):

Mithilfe des Skalarprodukts senkrechter Vektoren überprüft man die Aussage \(G \perp E, \, G \perp F\) (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).

 

\[\overrightarrow{n}_{G} \circ \overrightarrow{n}_{E} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{G} \perp \overrightarrow{E}, \; G \perp E\]

\[\overrightarrow{n}_{G} \circ \overrightarrow{n}_{F} = 0 \quad \Longleftrightarrow \quad \overrightarrow{n}_{G} \perp \overrightarrow{F}, \; G \perp F\]

 

\[\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}; \;\overrightarrow{n}_{F} = \begin{pmatrix} 1 \\ 0 \\ -5 \end{pmatrix}; \; \overrightarrow{n}_{G} = \begin{pmatrix} 5 \\ -4 \\ 1 \end{pmatrix}\]

 

\[\begin{pmatrix}  5 \\ -4 \\ 1\end{pmatrix} \circ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = 5 \cdot 1 + (-4) \cdot 2 + 1 \cdot 3 = 0\]

 

\[\Longrightarrow \quad G \perp E\]

 

\[\begin{pmatrix}  5 \\ -4 \\ 1\end{pmatrix} \circ \begin{pmatrix} 1 \\ 0 \\ -5 \end{pmatrix} = 5 \cdot 1 + (-4) \cdot 0 + 1 \cdot (-5) = 0\]

 

\[\Longrightarrow \quad G \perp F\]

Beispielaufgabe

Gegeben seien die Ebene \(E \colon 2x_{1} - 3x_{2} + x_{3} + 4 = 0\), die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 4 \\ -5 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\) und der Punkt \(P(0|-3|1)\).

Zeigen Sie, dass die Lotgerade \(\ell\) zur Ebene \(E\) durch den Punkt \(P\) ebenfalls Lotgerade zur Geraden \(g\) ist.

 

\[E \colon 2x_{1} - 3x_{2} + x_{3} + 4 = 0\]

\[g \colon \overrightarrow{X} = \begin{pmatrix} 4 \\ -5 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]

\[P(0|-3|1) \in \ell\]

 

Gleichung der Lotgerade \(\ell \perp E\)

Der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) ist Richtungsvektor der Lotgerade \(\ell\). Der Punkt \(P\) ist Aufpunkt der Lotgerade \(\ell\).

 

\[E \colon 2x_{1} - 3x_{2} + x_{3} + 4 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}\]

\[P(0|-3|1)\]

 

\[\Longrightarrow \quad \ell \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ -3 \\ 1 \end{pmatrix} + \mu \cdot \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\]

 

Nachweiß, dass die Lotgerade \(\ell \perp E\) auch Lotgerade zur Geraden \(g\) ist

Die Lotgerade \(\ell \perp E\) ist ebenfalls zur Gerade \(g\) eine Lotgerade, wenn sich \(\ell\) und \(g\) schneiden und wenn \(\ell \perp g\) gilt.

 

Nachweiß, dass sich \(\ell\) und \(g\) schneiden (vgl. Abiturskript - 2.3.1 Lagebeziehung von Geraden):

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 4 \\ -5 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]

\[\ell \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ -3 \\ 1 \end{pmatrix} + \mu \cdot \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\]

 

Ortsvektoren \(\overrightarrow{X}_{g}\) und \(\overrightarrow{X}_{\ell}\) der Geraden \(g\) und \(\ell\) gleichsetzen:

 

\[\begin{align*}\overrightarrow{X}_{g} &= \overrightarrow{X}_{\ell} \\[0.8em] \begin{pmatrix} 4 \\ -5 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix} &= \begin{pmatrix} 0 \\ -3 \\ 1 \end{pmatrix} + \mu \cdot \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}\end{align*}\]

 

Lineares Gleichungssystem formulieren:

 

\[\begin{align*} \text{I} & & & \quad \; 4 - 2\lambda = \qquad \enspace 2\mu \\[0.8em] \text{II} & & \wedge \enspace & -5 - \enspace \lambda = -3 - 3\mu \\[0.8em] \text{III} & & \wedge \enspace & \quad \; 1 + \enspace \lambda = \enspace \; 1 + \enspace \mu \end{align*}\]

 

Lineares Gleichungssystem lösen:

Gleichung III liefert \(\lambda = \mu\). Damit bietet sich das Einsetzverfahren an.

 

\[\begin{align*} \lambda = \mu \: \text{in I} \colon \; 4 - 2\mu &= 2\mu & &| + 2\mu \\[0.8em] 4 &= 4\mu & &| : 4 \\[0.8em] 1 &= \mu \end{align*}\]

 

\[\Longrightarrow \quad \lambda = 1\]

 

\[\begin{align*}\lambda = 1, \; \mu = 1 \; \text{in II (Probe)} \colon \; -5 - 1 &= -3 - 3 \cdot 1 \\[0.8em] -6 &= -6 \quad (\text{w}) \end{align*}\]

 

\(\Longrightarrow \quad\)Die Geraden \(\ell\) und \(g\) schneiden sich.

 

Nachweiß, dass \(\ell \perp g\) gilt:

Der Nachweiß kann mithilfe des Skalarprodukts senkrechter Vektoren erfolgen (vgl. Abiturskript - 2.1.3 Skalarprodukt von Vektoren, Anwendungen des Skalarprodukts).

 

\[g \colon \overrightarrow{X} = \begin{pmatrix} 4 \\ -5 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix}; \; \lambda \in \mathbb R\]

\[\ell \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ -3 \\ 1 \end{pmatrix} + \mu \cdot \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\]

 

\[\begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix} \circ \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix} = 2 \cdot (-2) + (-3) \cdot (-1) + 1 \cdot 1 = 0\]

 

\[\Longrightarrow \quad \ell \perp g\]

 

\(\Longrightarrow \quad\)Die Lotgerade \(\ell\) zur Ebene \(E\) durch den Punkt \(P\) ist ebenfalls Lotgerade zur Gerade \(g\).