Lotgerade zu zwei windschiefen Geraden
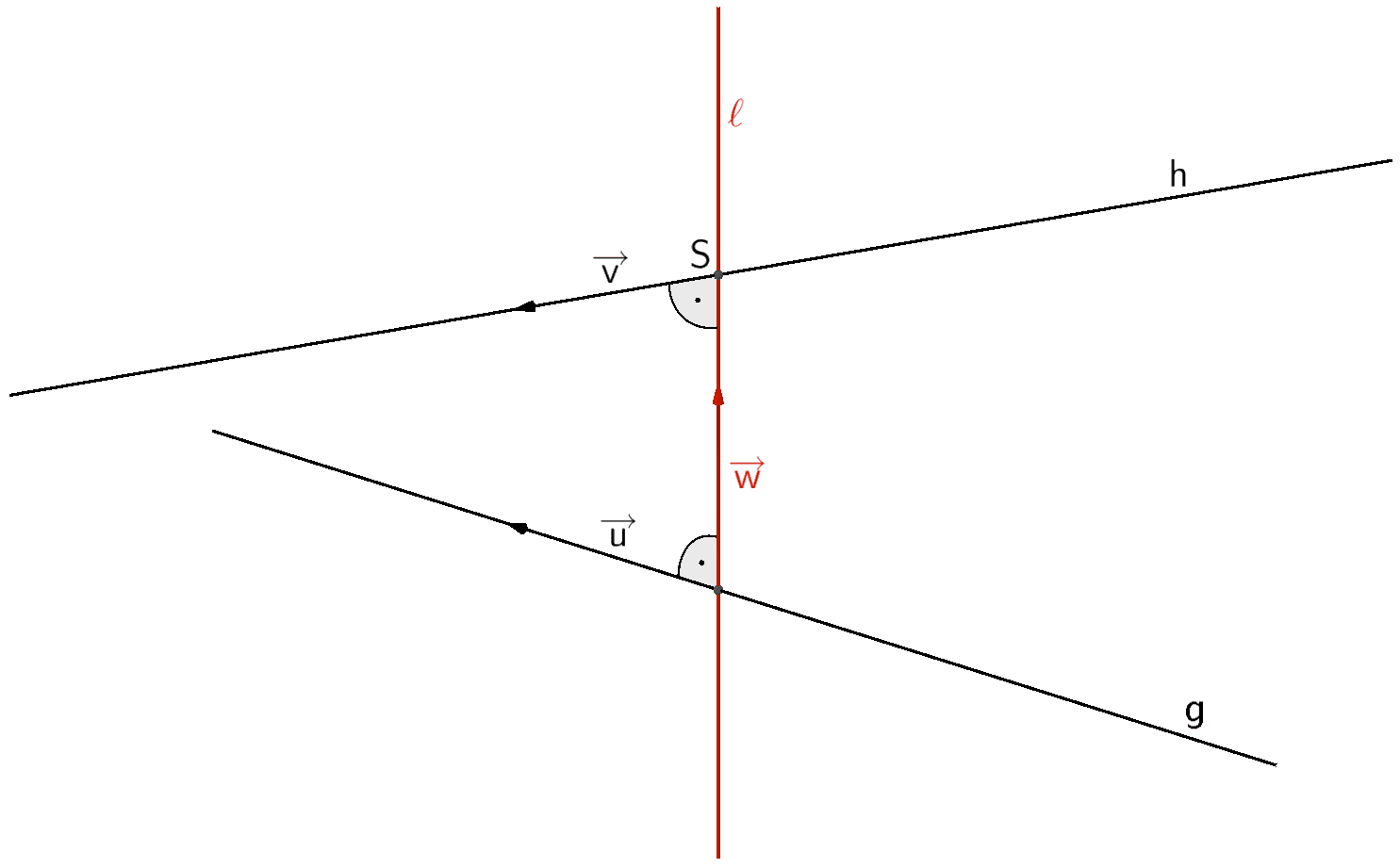
Diie Lotgerade \(\ell\) zu zwei windschiefen Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\,; \; \mu \in \mathbb R\) wird festgelegt durch einen Richtungsvektor \(\overrightarrow{w}\), der sowohl zum Richtungsvektor \(\overrightarrow{u}\) der Geraden \(g\) als auch zum Richtungsvektor \(\overrightarrow{v}\) der Gerade \(h\) senkrecht ist, und einen Schnittpunkt \(S\) der Lotgerade \(\ell\) mit der Gerade \(g\) oder mit der Gerade \(h\).
\[\ell \colon \overrightarrow{X} = \overrightarrow{S} + \tau \cdot \overrightarrow{w}\,; \; \tau \in \mathbb R\]
Richtungsvektor der Lotgerade \(\ell\)
Ein Richtungsvektor \(\overrightarrow{w}\) der Lotgerade \(\ell\) lässt sich mithilfe des Vektorprodukts der Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) der windschiefen Geraden \(g\) und \(h\) bestimmen (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).
\[\overrightarrow{w} = \overrightarrow{u} \times \overrightarrow{v}\]
Jedes Vielfache des Vektorprodukts \(\overrightarrow{u} \times \overrightarrow{v}\) ist ebenfalls ein Richtungsvektor \(\overrightarrow{w}\) der Lotgerade \(\ell\).
Aufpunkt der Lotgerade \(\ell\)
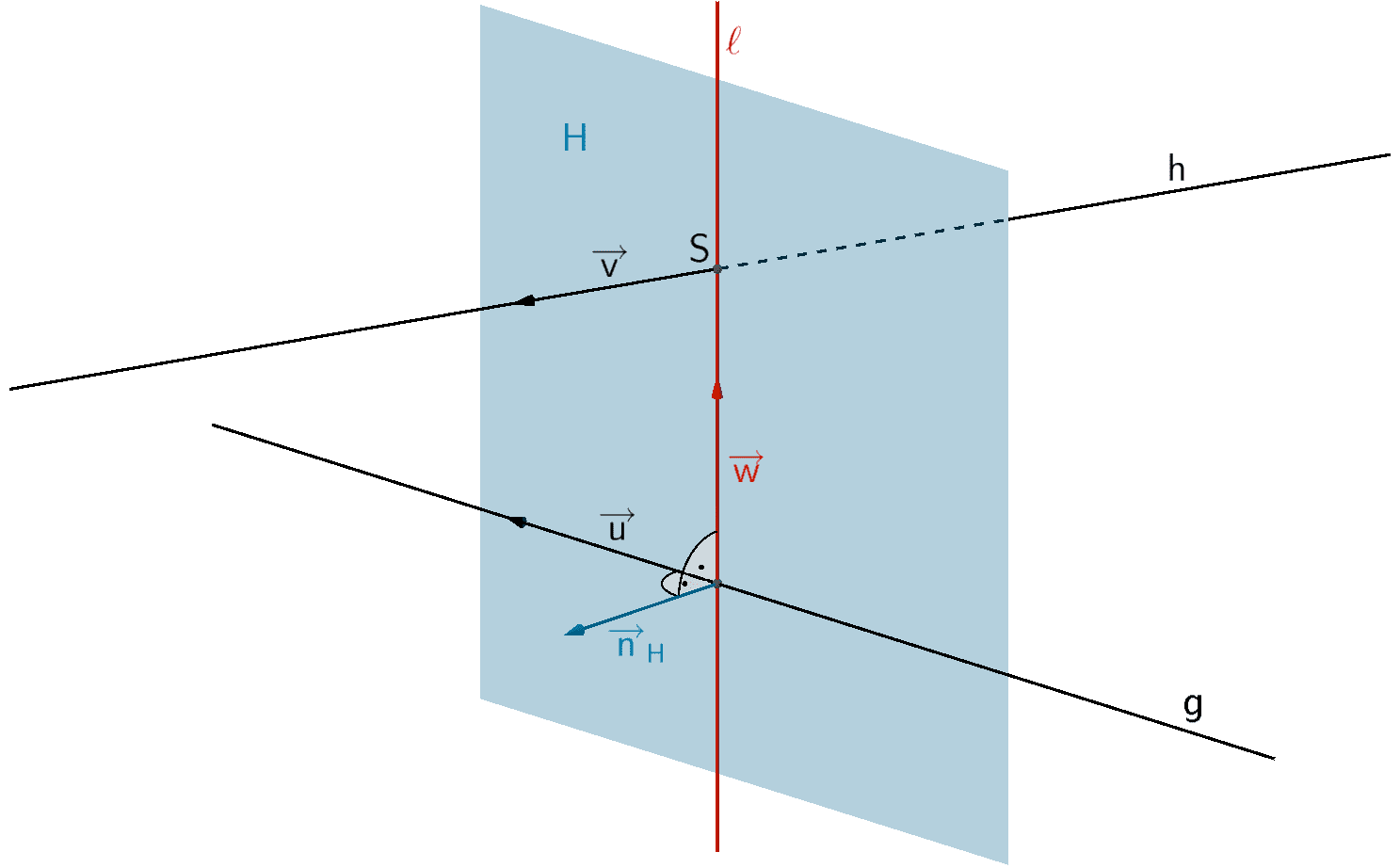
Als Aufpunkt für die Gleichung der Lotgerade \(\ell\) dient einer der beiden Schnittpunkte der Lotgerade mit einer der windschiefen Geraden, beispielsweise der Schnittpunkt \(S\) der Lotgerade \(\ell\) mit der Gerade \(h\).
Für die Bestimmung des Schnittpunkts \(S\) stellt man die Gleichung einer Hilfsebene \(H\) auf, welche die Gerade \(g\) und die Lotgerade \(\ell\) enthält. Man erhält den Normalenvektor \(\overrightarrow{n}_{H}\) der Hilfsebene \(H\) mithilfe des Vektorprodukts aus dem Richtungsvektor \(\overrightarrow{u}\) der Gerade \(g\) und dem Richtungsvektor \(\overrightarrow{w}\) der Lotgerade \(\ell\) (vgl. Abiturskript - 2.1.4 Vektorprodukt, Anwendungen des Vektorprodukts).
\[\overrightarrow{n}_{H} = \overrightarrow{u} \times \overrightarrow{w}\]
Jedes Vielfache des Vektorprodukts \(\overrightarrow{u} \times \overrightarrow{w}\) ist ebenfalls ein Normalenvektor \(\overrightarrow{n}_{H}\) der Hilfsebene \(H\).
Als Aufpunkt für die Gleichung der Hilfsebene \(H\) in Normalenform kommt jeder Punkt der Gerade \(g\) in Frage. Man wählt zweckmäßig den bekannten Aufpunkt \(A\) der Gerade \(g\).
\[H \colon \overrightarrow{n}_{H} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Schneidet man die Gerade \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\,; \; \mu \in \mathbb R\) und die Hilfsebene \(H\), erhält man genau den Wert des Parameters \(\mu\), der den Ortsvektor des Schnittpunkts \(S\) der Gerade \(h\) und der Lotgerade \(\ell\) festlegt (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene, Bestimmung des Schnittpunkts).
\[h \cap H \colon \overrightarrow{n}_{H} \circ (\overrightarrow{B} + \mu \cdot \overrightarrow{v} - \overrightarrow{A}) = 0\]
\(\Longrightarrow \quad\)Parameterwert für \(\mu\)
\(\Longrightarrow \quad\)Schnittpunkt \(S\) der Geraden \(h\) und der Lotgeraden \(\ell\)
\[\Longrightarrow \quad \ell \colon \overrightarrow{X} = \overrightarrow{S} + \tau \cdot \overrightarrow{w}\,; \; \tau \in \mathbb R\]
Beispiel:
Gegeben seien die windschiefen Geraden \(g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}; \; \mu \in \mathbb R\).
Bestimmen Sie eine Gleichung der Lotgerade \(\ell\) zu den Geraden \(g\) und \(h\).

Es gilt: \(\ell \perp g\), \(\ell \perp h\)
Es sei der Schnittpunkt \(S\) der Gerade \(h\) und der Lotgerade \(\ell\) der Aufpunkt der Lotgerade \(\ell\) und \(\overrightarrow{w}\) der Richtungsvektor der Lotgerade \(\ell\).
\[\ell \colon \overrightarrow{X} = \overrightarrow{S} + \tau \cdot \overrightarrow{w}\,; \; \tau \in \mathbb R\]
Richtungsvektor \(\overrightarrow{w}\) der Lotgerade \(\ell\)
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R \quad \Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}; \; \mu \in \mathbb R \quad \Longrightarrow \quad \overrightarrow{v} = \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}\]
\[\overrightarrow{w} = \overrightarrow{u} \times \overrightarrow{v} \quad \Longrightarrow \quad \overrightarrow{w} \perp \overrightarrow{u}, \; \overrightarrow{w} \perp \overrightarrow{v}\]
\[\begin{align*} \overrightarrow{u} \times \overrightarrow{v} &= \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \times \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 1 & \cdot & 0 & - & 0 & \cdot & 1 \\ 0 & \cdot & (-3) & - & 0 & \cdot & 0 \\ 0 & \cdot & 1 & - & 1 & \cdot & (-3) \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix} \\[0.8em] &= 3 \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{w} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]
Aufpunkt \(S\) der Lotgerade \(\ell\)

Der Schnittpunkt \(S\) der Gerade \(h\) und der Lotgerade \(\ell\) dient als Aufpunkt der Lotgerade \(\ell\). Die Hilfsebene \(H\) enthält die Gerade \(g\) und die Lotgerade \(\ell\). Sie schneidet die Gerade \(h\) im Schnittpunkt \(S\). Das Vektorprodukt \(\overrightarrow{u} \times \overrightarrow{w}\) liefert einen Normalenvektor \(\overrightarrow{n}_{H}\) der Hilfsebene \(H\).
\[g \subset H, \, \ell \subset H \quad \Longrightarrow \quad \overrightarrow{n}_{H} = \overrightarrow{u} \times \overrightarrow{w}\]
\[\overrightarrow{u} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \overrightarrow{w} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]
\[\begin{align*}\overrightarrow{n}_{H} &= \overrightarrow{u} \times \overrightarrow{w} \\[0.8em] &= \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 1 & \cdot & 1 & - & 0 & \cdot & 0 \\ 0 & \cdot & 0 & - & 0 & \cdot & 1 \\ 0 & \cdot & 0 & - & 1 & \cdot & 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \end{align*}\]
Als Aufpunkt für die Hilfsebene \(H\) kann der Aufpunkt der Gerade \(g\) verwendet werden.
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}; \; \lambda \in \mathbb R \quad \Longrightarrow \quad (2|-6|2) \in g\]
\[\Longrightarrow \quad H \colon \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} \right] = 0\]
\[\begin{align*} \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 2 \\ -6 \\ 2 \end{pmatrix} \right] &= 0 \\[0.8em] 1 \cdot (x_{1} - 2) + 0 \cdot (x_{2} + 6) + 0 \cdot (x_{3} - 2) &= 0 \\[0.8em] x_{1} - 2 &= 0 \end{align*}\]
\[\Longrightarrow \quad H \colon x_{1} - 2 = 0\]
Gerade \(h\) mit der Hilfsebene \(H\) schneiden und die Koordinaten des Schnittpunkts \(S\) berechnen (vgl. Abiturskript - 2.3.2 Lagebeziehung von Gerade und Ebene, Bestimmung des Schnittpunkts):
\[h \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix}; \; \mu \in \mathbb R\]
\[H \colon x_{1} - 2 = 0\]
\[\begin{align*} h \cap H \colon 6 - 3\mu - 2 &= 0 \\[0.8em] 4 - 3 \mu &= 0 & &| + 3\mu \\[0.8em] 4 &= 3\mu & &| : 3 \\[0.8em] \frac{4}{3} &= \mu \end{align*}\]
\[\overrightarrow{S} = \begin{pmatrix} 6 \\ -2 \\ 8 \end{pmatrix} + \frac{4}{3} \cdot \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ -\frac{2}{3} \\ 8 \end{pmatrix}\]
Gleichung der Lotgerade \(\ell\) formulieren:
\[\ell \colon \overrightarrow{X} = \overrightarrow{S} + \tau \cdot \overrightarrow{w}\,; \; \tau \in \mathbb R\]
\[\overrightarrow{S} = \begin{pmatrix} 2 \\ -\frac{2}{3} \\ 8 \end{pmatrix}; \; \overrightarrow{w} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]
\[\Longrightarrow \quad \ell \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ -\frac{2}{3} \\ 8 \end{pmatrix} + \tau \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}; \; \tau \in \mathbb R\]


