Randextremwert

Nach der Einnahme eines Medikaments wird die Konzentration \(K\) des Medikaments im Blut eines Patienten gemessen.

Die Funktion \(K \colon t \mapsto \dfrac{100t}{t^{2} + 25}\) mit \(t \geq 0\) beschreibt näherungsweise den Verlauf \(K(t)\) der Konzentration des Medikaments in Milligramm pro Liter in Abhängigkeit von der Zeit \(t\) in Stunden (vgl. Abbildung).

a) Bestimmen Sie den Zeitpunkt nach der Einnahme des Medikaments, zu dem die Konzentration \(K\) des Medikaments im Blut des Patienten noch 10 % der maximalen Konzentration beträgt auf Minuten genau.

(Teilergebnis: \(K'(t) = -\dfrac{100(t^{2} - 25)}{(t^{2} + 25)^{2}}\))

b) Berechnen Sie die mittlere Änderungsrate der Konzentration \(K\) im Zeitintervall \([10;20]\) und interpretieren Sie das Ergebnis im Sachzusammenhang.

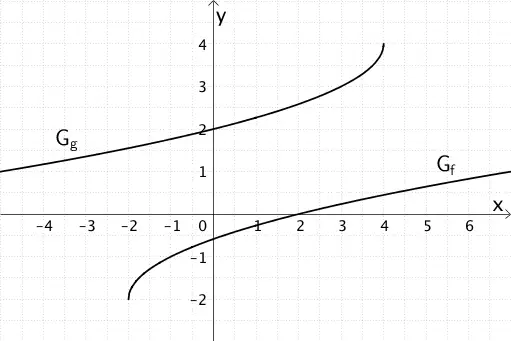
Die Abbildung zeigt je einen Ausschnitt des Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto \sqrt{x + 2} - 2\) und des Graphen \(G_{g}\) der Funktion \(g \colon x \mapsto -\sqrt{4 - x} + 4\).

a) Beschreiben Sie schrittweise wie der Graph \(G_{f}\) und der Graph \(G_{g}\) jeweils aus dem Graphen der Funktion \(x \mapsto \sqrt{x}\) hervorgeht und bestimmen Sie jeweils die maximale Definitionsmenge der Funktionen \(f\) und \(g\) durch Rechnung.

Betrachtet wird die Strecke \([PQ]\) der Punkte \(P(x|f(x))\) und \(Q(x|g(x))\) mit derselben Abszisse.

b) Zeigen Sie, dass der Funktionsterm \(d(x) = -\sqrt{4 - x} -\sqrt{x + 2} + 6\) die Länge der Strecke \([PQ]\) in Abhängigkeit der \(x\)-Koordinate des Punktes \(P\) bzw. \(Q\) beschreibt, und geben Sie die Definitionsmenge der Funktion \(d\) an.

c) Bestimmen Sie die \(x\)-Koordinate des Punktes \(P\) bzw. \(Q\), für die die Länge der Strecke \([PQ]\) minimal ist.

Die Gerade \(x = -1\) und die Gerade \(x = 3\) schließen mit den Graphen \(G_{f}\) und \(G_{g}\) ein Flächenstück mit dem Flächeninhalt \(A\) ein.

d) Der Flächeninhalt \(A\) soll zunächst näherungsweise berechnet werden. Hierfür wird das Viereck \(SPQR\) betrachtet, welches die Punkte \(S(-1|f(-1))\), \(P(3|f(3))\), \(Q(3|g(3))\) und \(R(-1|g(-1))\) festlegen. Der Schnittpunkt der Strecken \([PR]\) und \([QS]\) halbiert die Strecken jeweils.

Zeichnen Sie das Viereck \(SPQR\) in die Abbildung ein und schraffieren Sie das Flächenstück mit dem Flächeninhalt \(A\). Beschreiben Sie die wesentlichen Schritte eines geeigneten Lösungsverfahrens, um \(A\) näherungsweise zu berechnen.

e) Berechnen Sie den exakten Wert des Flächeninhalts \(A\).

f) Betrachtet wird nun die Integralfunktion \(\displaystyle I \colon x \mapsto \int_{0}^{x} d(t) dt\).

Geben Sie an, welche der folgenden Terme die Maßzahl des Flächeninhalts \(A\) berechnen (Falsche Antworten zählen negativ).

Unter den betrachteten Rechtecken gibt es eines mit größtem Flächeninhalt. Berechnen Sie die Seitenlängen dieses Rechtecks.

(5 BE)

Für jedes \(x \in \; ]0;4[\) wird der Abstand der vertikal übereinander liegenden Punkte \((x|q(x))\) und \((x|f(x))\) der Graphen von \(q\) bzw. \(f\) betrachtet, wobei in diesem Bereich \(q(x) > f(x)\) gilt. Der größte dieser Abstände ist ein Maß dafür, wie gut die Parabel den Graphen \(G_{f}\) im Bereich \(0 < x < 4\) annähert. Beschreiben Sie die wesentlichen Schritte, mithilfe derer man diesen größten Abstand rechnerisch bestimmen kann.

(3 BE)

Es gibt Punkte des Querschnitts der Tunnelwand, deren Abstand zu \(M\) minimal ist. Bestimmen Sie die \(x\)-Koordinaten der Punkte \(P_{x}\), für die \(d(x)\) minimal ist, und geben Sie davon ausgehend diesen minimalen Abstand an.

(5 BE)

Eine vertikal stehende Getränkedose hat die Form eines geraden Zylinders. Die Lage des gemeinsamen Schwerpunkts \(S\) von Dose und enthaltener Flüssigkeit hängt von der Füllhöhe der Flüssigkeit über dem Dosenboden ab. Ist die Dose vollständig gefüllt, so beträgt die Füllhöhe 15 cm.

Die bisher betrachtete Funktion \(f\) gibt für \(0 \leq x \leq 15\) die Höhe von \(S\) über dem Dosenboden in Zentimetern an; dabei ist \(x\) die Füllhöhe in Zentimetern (vgl. Abbildung 3).

Abb. 3

Berechnen Sie \(f(0)\) und \(f(15)\). Interpretieren Sie die beiden Ergebnisse im Sachzusammenhang.

(3 BE)

Die zunächst leere Dose wird langsam mit Flüssigkeit gefüllt, bis die maximale Füllhöhe von 15 cm erreicht ist. Beschreiben Sie mithilfe von Abbildung 2 die Bewegung des Schwerpunkts \(S\) während des Füllvorgangs. Welche Bedeutung im Sachzusammenhang hat die Tatsache, dass \(x\)-Koordinate und \(y\)-Koordinate des Tiefpunkts von \(G_f\) übereinstimmen?

(3 BE)