Die Ursprungsgerade \(h\) mit der Gleichung \(y = \frac{2}{e^2} \cdot x\) schließt mit \(G_f\) für \(x \geq 0\) ein Flächenstück mit dem Inhalt \(B\) vollständig ein.
Berechnen Sie die \(x\)-Koordinaten der drei Schnittpunkte der Geraden \(h\) mit \(G_f\) und zeichnen Sie die Gerade in Abbildung 2 ein. Berechnen Sie \(B\).
(6 BE)
Lösung zu Teilaufgabe 1e
\[f(x) = 2x \cdot e^{-0{,}5x^2}\,; \quad D = \mathbb R\]
\[h\;\colon \, y = \frac{2}{e^2} \cdot x\]
Schnittpunkte der Geraden \(h\) mit \(G_f\)
Gleichsetzen der Fubktionsterrme:
\[\begin{align*} 2x \cdot e^{-0{,}5x^2} &= \frac{2}{e^2} \cdot x & &| - \frac{2}{e^2} \cdot x \\[0.8em] 2x \cdot e^{-0{,}5x^2} - \frac{2}{e^2} \cdot x &= 0 \\[0.8em] 2x \left( e^{-0{,}5x^2} - e^{-2} \right) &= 0 \end{align*}\]
\[\Longrightarrow \quad x_1 = 0 \enspace \vee \enspace e^{-0{,}5x^2} - e^{-2} = 0\]
\[\begin{align*} e^{-0{,}5x^2} - e^{-2} &= 0 & &| + e^{-2} \\[0.8em] e^{-0{,}5x^2} &= e^{-2} & &| \; \text{Exponentenvergleich} \\[0.8em] -0{,}5x^2 &= -2 & &| : (-0{,}5) \\[0.8em] x^2 &= 4 & &| \; \sqrt{\quad} \\[0.8em] x_{2,3} &= \pm 2 \end{align*}\]
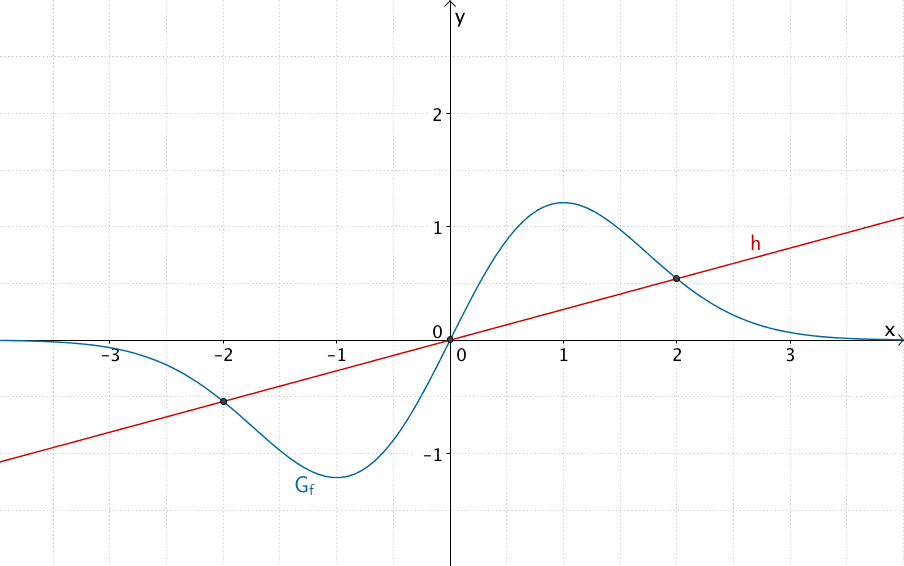
Die Gerade \(h\) schneidet \(G_f\) an den Stellen \(x_1 = 0\), \(x_2 = -2\) und \(x_3 = 2\).
Flächeninhalt \(B\)
1. Lösungsansatz: Differenz zweier Flächeninhalte
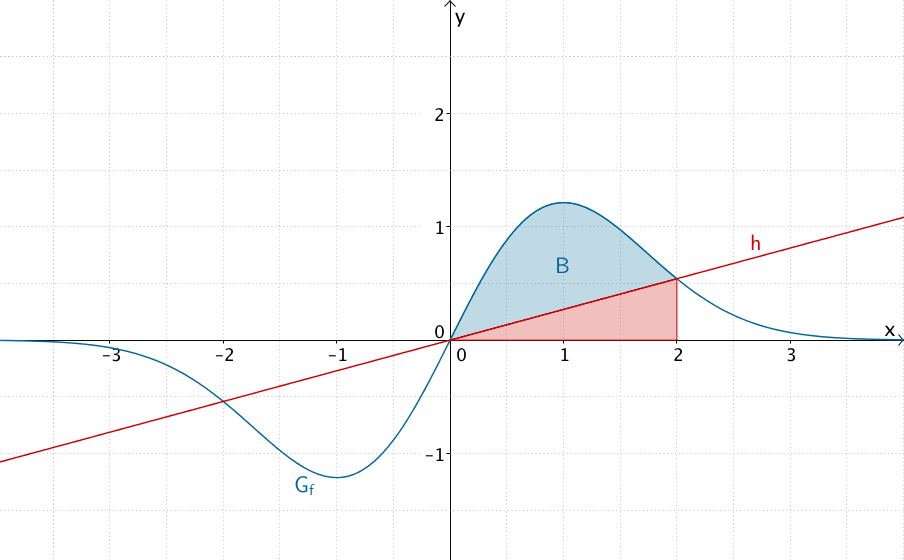
Der Flächeninhalt \(B\) errechnet sich aus der Differenz des Flächeninhalts \(A(2)\) (siehe Teilaufgabe 1d) und dem Flächeninhalt des rechtwinkligen Dreiecks, das die Gerade \(h\) im Intervall \(x \in [0;2]\) mit der \(x\)-Achse einschließt.
\(A(u) = 2 - 2e^{-0{,}5u^2}\) (siehe Teilaufgabe 1d)
\[f(x) = 2x \cdot e^{-0{,}5x^2}\]
\[\begin{align*} B &= A(2) - \frac{1}{2} \cdot 2 \cdot f(2) \\[0.8em] &= 2 - 2e^{-0{,}5 \cdot 2^2} - \frac{1}{2} \cdot 2 \cdot 2 \cdot 2 \cdot e^{-0{,}5 \cdot 2^2} \\[0.8em] &= 2 - 2e^{-2} - 4e^{-2} \\[0.8em] &= 2 - \frac{6}{e^2} \\[0.8em] &\approx 1{,}19 \end{align*}\]
Der Flächeninhalt \(B\) beträgt 1,19 FE (Flächeneinheiten).
2. Lösungsansatz: Fläche zwischen zwei Funktionsgraphen
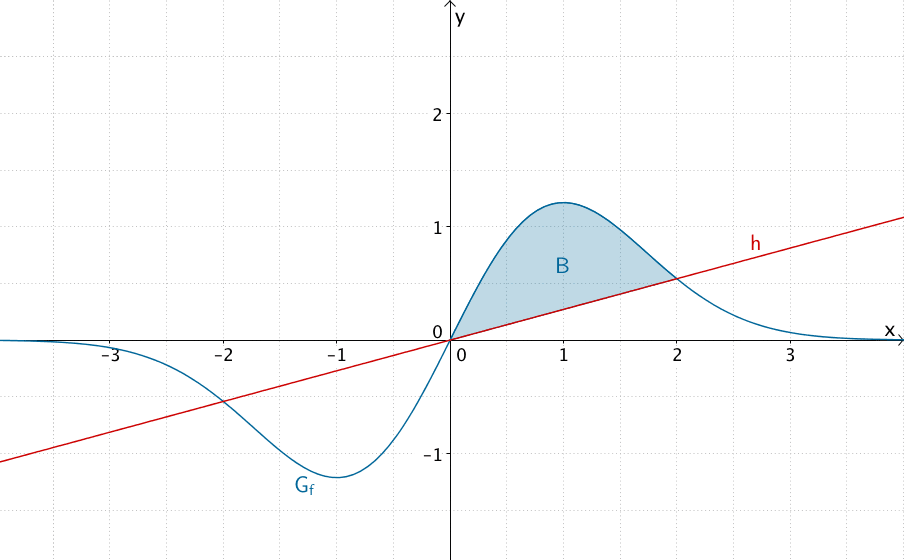
Der Flächeninhalt \(B\) des Flächenstücks, das der Graph von \(f\) mit der Geraden \(h\) für \(x \geq 0\) einschließt, ist gleich dem Wert des bestimmten Integrals \(\displaystyle \int_0^2 (f(x) - h(x))\,dx\).
\[f(x) = 2x \cdot e^{-0{,}5x^2}\,; \quad D = \mathbb R\]
\[h(x) = \frac{2}{e^2} \cdot x\]
\[B = \int_0^2 \left( 2x \cdot e^{-0{,}5x^2} - \frac{2}{e^2} \cdot x \right)\,dx\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Stammfunktion \(F(x)\) von \(f(x)\) und \(H(x)\) von \(h(x)\) bestimmen:
\(\displaystyle f(x) = 2x \cdot e^{-0{,}5x^2} = -2 \cdot (-x) \cdot e^{-0{,}5x^2} \) (siehe Teilaufgabe 1d)
Wichtiges unbestimmtes Integral:
\[\int f'(x) \cdot e^{f(x)}dx = e^{f(x)} + C\]
(vgl. Merkhilfe)
\[F(x) = -2 \cdot e^{-0{,}5x^2} + C\]
\[h(x) = \frac{2}{e^2} \cdot x\]
Stammfunktion einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad F(x) = \frac{1}{r + 1} \cdot x^{r + 1} + C\]
\[r \neq -1\]
\[H(x) = \frac{2}{e^2} \cdot \frac{1}{2}x^2 + C = \frac{x^2}{e^2} + C\]
Flächeninhalt \(B\) berechnen:
\[\begin{align*} B &= \int_0^2 (f(x) - h(x))\,dx \\[0.8em] &= \int_0^2 \left( 2x \cdot e^{-0{,}5x^2} - \frac{2}{e^2} \cdot x \right)\,dx \\[0.8em] &= \left[ -2 \cdot e^{-0{,}5x^2} - \frac{x^2}{e^2} \right]_0^2 \\[0.8em] &= -2 \cdot e^{-0{,}5 \cdot 2^2} - \frac{2^2}{e^2} - \left( -2 \cdot e^{-0{,}5 \cdot 0^2} - \frac{0^2}{e^2} \right) \\[0.8em] &= -\frac{2}{e^2} - \frac{4}{e^2} + 2 \\[0.8em] &= -\frac{6}{e^2} + 2 \\[0.8em] &\approx 1{,}19 \end{align*}\]
Der Flächeninhalt \(B\) beträgt 1,19 FE (Flächeneinheiten).

