Berechnen Sie \(f(4)\), im Hinblick auf eine der folgenden Aufgaben auf zwei Dezimalen genau, und zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse \(G_{f}\) im Bereich \(-4 \leq x \leq 4\) in das Koordinatensystem aus Aufgabe 1e ein.
(4 BE)
Lösung zu Teilaufgabe 1f
Funktionswert berechnen, Funktionsgraph zeichnen
\[f(x) = e^{\frac{1}{2}x} + e^{-\frac{1}{2}x}; \; D = \mathbb R\]
Funktionswert \(f(4)\)
\[f(4) = e^{\frac{1}{2} \cdot 4} + e^{-\frac{1}{2} \cdot 4} = e^{2} + e^{-2} \approx 7{,}52\]
Zeichnen von \(G_{f}\) unter Berücksichtigung der bisherigen Ergebnisse
Bisherige Ergebnisse:
- \(G_{f}\) ist achsensymmetrisch zur \(y\)-Achse und verläuft oberhalb der \(x\)-Achse. (vgl. Teilaufgabe 1a,b)
- Schnittpunkt mit der \(y\)-Achse \(S_{y}(0|2)\) ist Tiefpunkt \(TiP(0|2)\) von \(G_{f}\) (vgl. Teilaufgabe 1b,d)
- \(G_{f}\) ist in \(\mathbb R\) linksgekrümmt (vgl. Teilaufgabe 1c).
- \(G_{f}\) verläuft für \(x \to \pm \infty\) gegen \(+\infty\) (vgl. Teilaufgabe 1b).
- Steigung der Tangente \(g\) an \(G_{f}\) im Punkt \(P(2|3{,}1)\): \(m_{g} = 1{,}2\) (vgl. Teilaufgabe 1e).
- \(G_{f}\) verläuft durch den Punkt \((4|7{,}52)\) (vgl. oben).
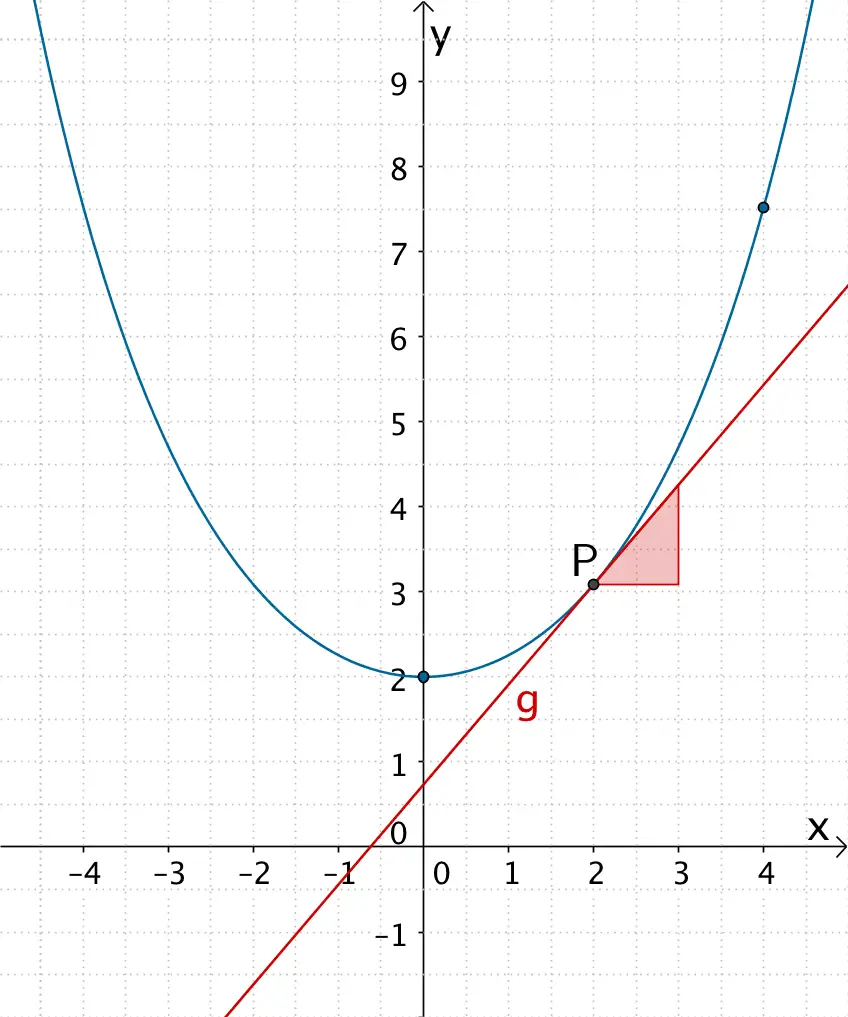
Graph der Funktion \(f \colon x \mapsto e^{\frac{1}{2}x} + e^{-\frac{1}{2}x}\) und Tangente \(g\) an \(G_{f}\) im Punkt \(P\)


