Weisen Sie nach, dass die Steigung von \(G_f\) in jedem Punkt des Graphen negativ ist. Berechnen Sie die Größe des Winkels, unter dem \(G_f\) die \(x\)-Achse schneidet.
(4 BE)
Lösung zu Teilaufgabe 1b
Nachweis, dass die Steigung von \(G_f\) in jedem Punkt des Graphen negativ ist
Es ist nachzuweisen, dass die Steigung einer Tangente \(T\) an \(G_f\) für alle \(x \in D_{f}\) negativ ist.
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\(m_{T} < 0 \quad \Longrightarrow \quad f'(x) < 0\) für alle \(x \in D_{f}\)
Erste Ableitung \(f'\) bilden:
\[f(x) = \frac{20x}{x^2 - 25}\,; \quad D_{f} = \mathbb R \,\backslash\,\{-5;5\}\]
Quotientenregel
\[ f(x) = \frac{u(x)}{v(x)} \quad \Longrightarrow \quad f'(x) = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{[v(x)]^2}\]
Ableitung einer Potenzfunktionen
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\begin{align*} f'(x) &= \frac{20 \cdot (x^2 -25) - 20x \cdot 2x}{(x^2 - 25)^2} \\[0.8em] &= \frac{20 \cdot (x^2 -25 -2x^2)}{(x^2 - 25)^2} \\[0.8em] &= \frac{20 \cdot (-x^2 - 25)}{(x^2 - 25)^2} \\[0.8em] &= -\frac{20 \cdot \overbrace{(x^2 + 25)}^{> \, 0}}{\underbrace{(x^2 - 25)^2}_{> \, 0}} \end{align*}\]
\(\Longrightarrow \quad f'(x) < 0\) für alle \(x \in D_{f}\)
\(\Longrightarrow \quad\) Die Steigung von \(G_{f}\) ist in jedem Punkt des Graphen negativ.
Größe des Winkels, unter dem \(G_f\) die \(x\)-Achse schneidet
Der Winkel unter dem \(G_f\) die \(x\)-Achse schneidet lässt sich mithilfe der Steigung der Tangente \(T\) an \(G_f\) im Punkt \(N\,(0|0)\), also an der Nullstelle von \(f\) (siehe Teilaufgabe 1a) berechnen.
Steigungswinkel \(\alpha\) einer Gerade \(g \colon y = m \cdot x +t\)
\[\tan \alpha = m \qquad \alpha \neq 90^\circ\]
\[\tan {\alpha} = m_{T}\]
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[\tan {\alpha} = m_{T} = f'(0)\]
\[f'(x) = -\frac{20 \cdot (x^2 + 25)}{(x^2 - 25)^2}\]
\[f'(0) = -\frac{20 \cdot (0^2 + 25)}{(0^2 - 25)^2} = - \frac{20 \cdot 25}{(-25)^2} = -\frac{20}{25} = -\frac{4}{5}\]
\[\begin{align*}\tan{\alpha} &= -\frac{4}{5} & &| \; \tan^{-1}(\dots) \\[0.8em] \alpha &\approx -38{,}66^{\circ}\end{align*}\]
\(G_{f}\) schneidet die \(x\)-Achse unter einem Winkel von 38,66°.
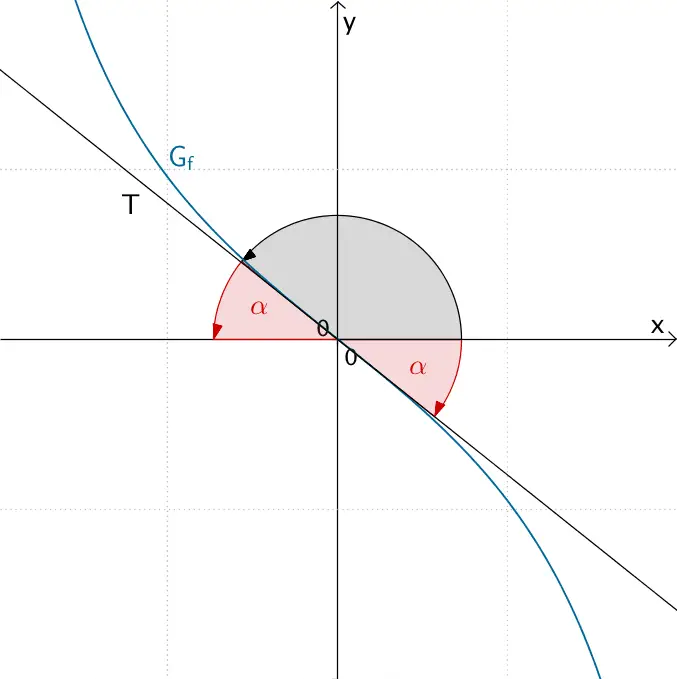
Schnittwinkel \(\alpha\), unter dem \(G_{f}\) die \(x\)-Achse im Koordinatenursprung schneidet
Anmerkung: Eine Gerade schließt mit der \(x\)-Achse zwei Winkel ein. Unter dem Schnittwinkel versteht man den spitzen Winkel. Er wird stets positiv angegeben. Über die Beziehung \(\tan{\alpha} = m\) bzw. \(\tan{\alpha} = f'(x_{0})\) lässt sich der Steigungswinkel berechnen. Der Steigungswinkel ist der in mathematisch positivem Sinn (gegen den Uhrzeigersinn) gemessene Winkel, den die Gerade mit der positiven \(x\)-Achse einschließt. Bei einer negativen Steigung der Geraden, gibt der Taschenrechner mit der Inversfunktion \((\tan^{-1})\) den Winkel in mathematisch negativem Sinn (im Uhrzeigersinn) aus, weil der Tangens nur für \(-90^{\circ} < \alpha < +90^{\circ}\) definiert ist. Um den Steigungswinkel in mathematisch positivem Sinn zu erhalten, addiert man zum Ergebnis 180°. Für den Schnittwinkel gibt man das Ergebnis positiv an. Im Falle einer positiven Steigung der Geraden stimmen der Schnittwinkel und der Steigungswinkel überein. Sonderfälle sind senkrechte Geraden \((\alpha = 90^{\circ})\) und waagrechte Geraden \((\alpha = 0^{\circ})\).


