Erstellen Sie zu dem beschriebenen Sachverhalt für den Fall, dass das Ereignis \(E\) mit einer Wahrscheinlichkeit von 98 % eintritt, eine vollständig ausgefüllte Vierfeldertafel. Bestimmen Sie für diesen Fall die Wahrscheinlichkeit \(P_{S}(M)\).
(5 BE)
Lösung zu Teilaufgabe 1c
Vierfeldertafel der Wahrscheinlichkeiten, Bedingte Wahrscheinlichkeit
Vierfeldertafel
\[P(E) = 0{,}98\]
Die Wahrscheinlichkeiten der Ereignisse \(M\) und \(S\) sind bereits aus Teilaufgabe 1b bekannt:
\[P(M) = 0{,}9\,; \enspace P(S) = 0{,}24\]
Wahrscheinlichkeiten der Gegenereignisse \(\overline{M}\) und \(\overline{S}\):
\[P(\overline{M}) = 1 - P(M) = 1 - 0{,}9 = 0{,}1\]
\[P(\overline{S}) = 1 - P(S) = 1 - 0{,}24 = 0{,}76\]
Vierfeldertafel der Wahrscheinlichkeiten:
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(P(M \cap S)\) | \(P(\overline{M} \cap S)\) | \(0{,}24\) |
| \(\overline{S}\) | \(P(M \cap \overline{S})\) | \(P(\overline{M} \cap \overline{S})\) | \(0{,}76\) |
| \(0{,}9\) | \(0{,}1\) | \(1\) |
Um die Vierfeldertafel vollständig ausfüllen zu können, muss eine der Schnittmengenwahrscheinlichkeiten (Wahrscheinlichkeit eines Elementarereignisses) bekannt sein.
Aus Teilaufgabe 1a ist bekannt:
\[\begin{align*}E &= M \cup S \\[0.8em] &= (M \cap S) \cup (M \cap \overline{S}) \cup (\overline{M} \cap S) \end{align*}\]
\[\begin{align*}\Longrightarrow \quad P(E) &= P(M \cup S) \\[0.8em] &= P(M \cap S) + P(M \cap \overline{S}) + P(\overline{M} \cap S) \end{align*}\]
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(P(M \cap S)\) | \(P(\overline{M} \cap S)\) | \(0{,}24\) |
| \(\overline{S}\) | \(P(M \cap \overline{S})\) | \(P(\overline{M} \cap \overline{S})\) | \(0{,}76\) |
| \(0{,}9\) | \(0{,}1\) | \(1\) |
Wahrscheinlichkeit des Ereignisses \(E\) (grau hinterlegte Einträge)
\[P(E) = 0{,}98\]
\[P(\overline{E}) = P(\overline{M} \cap \overline{S}) = 1 - P(E) = 1 - 0{,}98 = 0{,}02\]
Als Alternative lässt sich ein Gesetz von de Morgan anwenden:
\(P(E) = P(M \cup S)\) (siehe Teilaufgabe 1a)
Gesetze von de Morgan
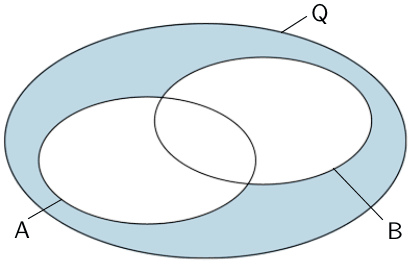
Weder Ereignis \(A\) noch Ereignis \(B\); Keines der beiden Ereignisse
\[\overline{A} \cap \overline{B} = \overline{A \cup B}\]
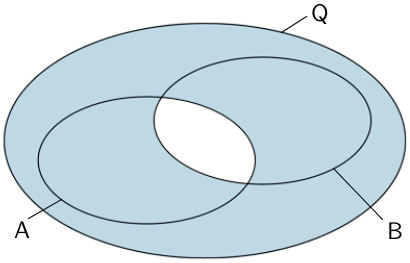
Nicht beide Ereignisse \(A\) und \(B\) zugleich; Höchstens eines der beiden Ereignisse
\[\overline{A \cap B} = \overline{A} \cup \overline{B}\]
\[\begin{align*} \Longrightarrow \quad P(\overline{E}) &= P(\overline{M \cup S}) & &| \; \overline{M \cup S} = \overline{M} \cap \overline{S} \\[0.8em] &= P(\overline{M} \cap \overline{S}) \end{align*}\]
\[P(\overline{E}) = P(\overline{M} \cap \overline{S}) = 1 - P(E) = 1 - 0{,}98 = 0{,}02\]
Als weitere Alternative kann der Additionssatz angewendet werden:
\(P(E) = P(M \cup S)\) (siehe Teilaufgabe 1a)
Additionssatz
Für zwei beliebige Ereignisse \(A\) und \(B\) gilt:
\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]
\(P(M) = 0{,}9\,; \enspace P(S) = 0{}24\) (siehe Teilaufgabe 1b)
\[P(E) = 0{,}98\]
\(\begin{align*}P(E) &= P(M \cup S) & &| \; \text{Additionssatz anwenden} \\[0.8em] &= P(M) + P(S) - P(M \cap S) & &| + P(M \cap S) \enspace - P(E) \\[0.8em] P(M \cap S) &= P(M) + P(S) - P(E) \\[0.8em] &= 0{,}9 + 0{,}24 - 0{,}98 \\[0.8em] &= 0{,}16 \end{align*}\)
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(0{,}16\) | \(P(\overline{M} \cap S)\) | \(0{,}24\) |
| \(\overline{S}\) | \(P(M \cap \overline{S})\) | \(0{,}02\) | \(0{,}76\) |
| \(0{,}9\) | \(0{,}1\) | \(1\) |
Es ist ausreichen, eine der Schnittmengenwahrscheinlichkeiten zu berechnen. Die Vierfeldertafel kann anschließend mittels Subtraktion vervollständigt werden.
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(P(M \cap S)\) | \(P(\overline{M} \cap S)\) | \(0{,}24\) |
| \(\overline{S}\) | \(P(M \cap \overline{S})\) | \(0{,}02\) | \(0{,}76\) |
| \(0{,}9\) | \(0{,}1\) | \(1\) |
\[P(\overline{M} \cap S) = P(\overline{M}) - P(\overline{M} \cap \overline{S}) = 0{,}1 - 0{,}02 = 0{,}08\]
\[P(M \cap \overline{S}) = P(\overline{S}) - P(\overline{M} \cap \overline{S}) = 0{,}76 - 0{,}02 = 0{,}74\]
\[P(M \cap S) = P(S) - P(\overline{M} \cap S) = 0{,}24 - 0{,}08 = 0{,}16\]
oder
\[P(M \cap S) = P(M) - P(M \cap \overline{S}) = 0{,}9 - 0{,}74 = 0{,}16\]
bzw.
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(0{,}16\) | \(P(\overline{M} \cap S)\) | \(0{,}24\) |
| \(\overline{S}\) | \(P(M \cap \overline{S})\) | \(P(\overline{M} \cap \overline{S})\) | \(0{,}76\) |
| \(0{,}9\) | \(0{,}1\) | \(1\) |
\[P(M \cap \overline{S}) = P(M) - P(M \cap S) = 0{,}9 - 0{,}16 = 0{,}74\]
\[P(\overline{M} \cap S) = P(S) - P(M \cap S) = 0{,}24 - 0{,}16 = 0{,}08\]
\[P(\overline{M} \cap \overline{S}) = P(\overline{M}) - P(\overline{M} \cap S) = 0{,}1 - 0{,}08 = 0{,}02\]
oder
\[P(\overline{M} \cap \overline{S}) = P(\overline{S}) - P(M \cap \overline{S}) = 0{,}76 - 0{,}74 = 0{,}02\]
| \(M\) | \(\overline{M}\) | ||
| \(S\) | \(0{,}16\) | \(0{,}08\) | \(0{,}24\) |
| \(\overline{S}\) | \(0{,}74\) | \(0{,}02\) | \(0{,}76\) |
| \(0{,}9\) | \(0{,}1\) | \(1\) |
Wahrscheinlichkeit \(P_{S}(M)\)
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
Der Vierfeldertafel entnimmt man die Wahrscheinlichkeiten \(P(M \cap S)\). Die Wahrscheinlichkeit \(P(S)\) ist aus Teilaufgabe 1b bekannt.
\[P(M \cap S) = 0{,}16\,; \enspace P(S) = 0{,}24\]
\[P_{S}(M) = \frac{P(M \cap S)}{P(S)} = \frac{0{,}16}{0{,}24} = \frac{2}{3}\]


