Der Anbaubetrieb sät 200 Samenkörner der Qualität B. Bestimmen Sie die Wahrscheinlichkeiten folgender Ereignisse:
\(E\): „Von den gesäten Samenkörnern keimen genau 140."
\(F\): „Von den gesäten Samenkörnern keimen mehr als 130 und weniger als 150."
(3 BE)
Lösung zu Teilaufgabe b
Binomialverteilung, binomialverteilte Zufallsgröße
Die Wahrscheinlichkeit dafür, dass ein Samenkorn der Qualität B keimt ist mit \(p = 0{,}7\) konstant (vgl. Angabe). Da nur zwischen den beiden sich gegenseitig ausschließenden Ereignissen „Samenkorn der Qualität B keimt" und „Samenkorn der Qualität B keimt nicht" unterschieden wird, liegt ein Bernoulli-Experiment vor.
Bernoulli-Experiment, Bernoulli-Kette
Ein Zufallsexperiment, bei dem nur zwei verschiedene sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können, heißt Bernoulli-Experiment.
Das Eintreten des Ereignisses \(A\) wird als Treffer und das Eintreten des Gegeneignisses \(\overline{A}\) wird als Niete bezeichnet. Die Trefferwahrscheinlichkeit \(P(A)\) bezeichnet man mit \(\boldsymbol{p}\) und die Wahrscheinlichkeit für eine Niete mit \(q = 1- p\). Wird ein Bernoulli-Experiment \(n\)-mal wiederholt, spricht man von einer Bernoulli-Kette der Länge \(\boldsymbol{n}\). Dabei müssen die einzelnen Wiederholungen unabhängig voneinander erfolgen. Das heißt, die Trefferwahrscheinlichkeit \(p\) bleibt konstant.
Das Aussäen von 200 Samenkörnern der Qualität B entspricht der Länge der Bernoulli-Kette \(n = 200\).
Es sei \(X\) die Zufallsgröße, welche die Anzahl der keimenden Samenkörner unter den gesäten Samenkörnern der Qualität B beschreibt.
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
Die Zufallsgröße \(X\) ist nach \(B(200;0{,}7)\) binomialverteilt.
Wahrscheinlichkeit des Ereignisses \(E\)
\(E\): „Von den gesäten Samenkörnern keimen genau 140."
Gesucht ist die Wahrscheinlichkeit \(P_{0{,}7}^{200}(X = 140)\). Die Wahrscheinlichkeit lässt sich mithilfe des Stochastischen Tafelwerks (ST) ermitteln.
\(p = 0{,}7\), \(n = 200\), \(k = 140\)
\[\begin{align*}P(E) &= P_{0{,}7}^{200}(X = 140) \\[0.8em] &= B(200;0{,}7;140) \\[0.8em] &\overset{\text{ST}}{=} 0{,}06146 \\[0.8em] &\approx 6{,}15\,\% \end{align*}\]
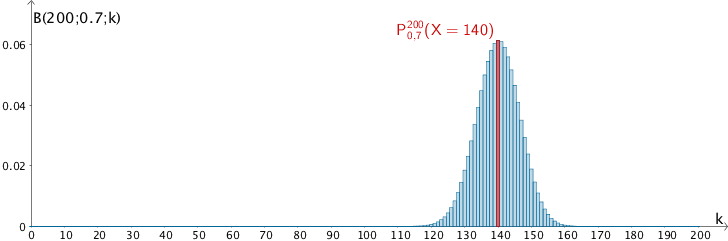
Wahrscheinlichkeitsverteilung der nach \(B(200;0{,}7)\) binomialverteilten Zufallsgröße \(X\), Wahrscheinlichkeit \(P_{0{,}7}^{200}(X = 140)\)
Wahrscheinlichkeit des Ereignisses \(F\)
\(F\): „Von den gesäten Samenkörnern keimen mehr als 130 und weniger als 150."
Gesucht ist die Wahrscheinlichkeit \(P_{0{,}7}^{200}(130 < X < 150)\). Die Wahrscheinlichkeit lässt sich auf die kumulative Verteilungsfunktion zurückführen, sodass das Stochastische Tafelwerk (ST) verwendet werden kann.
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
\(p = 0{,}7\), \(n = 200\)
\[\begin{align*} P(F) &= P_{0{,}7}^{200}(130 < X < 150) \\[0.8em] &= P_{0{,}7}^{200}(131 \leq X \leq 149) \\[0.8em] &= P_{0{,}7}^{200}(X \leq 149) - P_{0{,}7}^{200}(X \leq 130) \\[0.8em]&= \sum \limits_{i\,=\,0}^{149}B(200;0{,}7;i) - \sum \limits_{i\,=\,0}^{130}B(200;0{,}7;i) \\[0.8em] &\overset{\text{ST}}{=} 0{,}93045 - 0{,}07279 \\[0.8em] &= 0{,}85766 \\[0.8em] &\approx 85{,}77\,\% \end{align*}\]
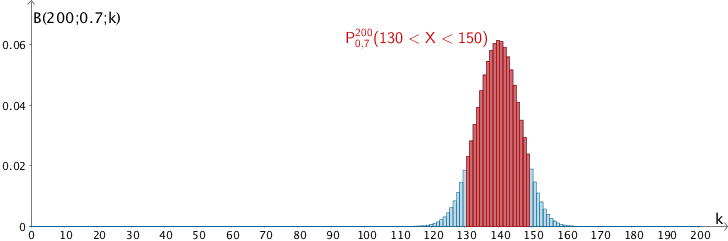
Wahrscheinlichkeitsverteilung der nach \(B(200;0{,}7)\) binomialverteilten Zufallsgröße \(X\), Wahrscheinlichkeit \(P_{0{,}7}^{200}(130 < X < 150)\)


