Gegeben ist die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}\) mit \(\lambda \in \mathbb R\).
Zeigen Sie, dass \(g\) in der Ebene mit der Gleichung \(x_1 + x_2 + x_3 = 2\) liegt.
(2 BE)
Lösung zu Teilaufgabe a
\[g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}, \;\lambda \in \mathbb R\]
Ebene: \(x_1 + x_2 + x_3 = 2\)
1. Möglichkeit: Ansatz für die Bestimmung der gemeinsamen Punkte von \(g\) und der Ebene
Hierfür werden die Koordinaten der Geradengleichung von \(g\) in die Gleichung der Ebene eingesetzt. Ergibt die Gleichung eine wahre Aussage (Parameter entfällt), gibt es unendlich viele gemeinsame Punkte der Gerade \(g\) und der Ebene und die Gerade \(g\) liegt somit in der Ebene.
\[g \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} = \textcolor{#e9b509}{\begin{pmatrix} \lambda \\ 1 \\ 1 - \lambda \end{pmatrix}}, \;\lambda \in \mathbb R\]
\[\begin{align*}g \cap \text{Ebene}\colon\, \textcolor{#e9b509}{\lambda} + \textcolor{#e9b509}{1} + \textcolor{#e9b509}{1 - \lambda} &= 2 \\[0.8em] 2 &= 2 &&(\text{w})\end{align*}\]
Folglich liegt die Gerade \(g\) in der Ebene.
2. Möglichkeit: Skalarprodukt orthogonaler Vektoren anwenden
Die Gerade \(g\) liegt in der Ebene, wenn der Richtungsvektor von \(g\) und der Normalenvektor der Ebene zueinander senkrecht (orthogonal) sind und der Aufpunkt der Geradengleichung von \(g\) in der Ebene liegt.
(Vgl. ![]() Untersuchung der Lagebeziehung zwischen Gerade und Ebene)
Untersuchung der Lagebeziehung zwischen Gerade und Ebene)
Gleichung einer Gerade / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[g \colon \overrightarrow{X} = \textcolor{#e9b509}{\begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}} + \lambda \cdot \textcolor{#cc071e}{\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}}, \;\lambda \in \mathbb R\]
Ebenengleichung in Normalenform (vgl. Merkhilfe)
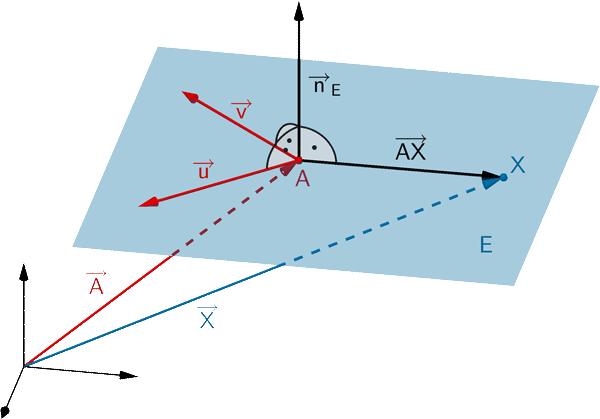
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Ebene: \(x_1 + x_2 + x_3 = 2 \; \Rightarrow \; \textcolor{#0087c1}{\overrightarrow{n} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}}\)
Der Richtungsvektor von \(g\) und der Normalenvektor der Ebene sind zueinander senkrecht, wenn das Skalarprodukt der Vektoren null ist.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\textcolor{#cc071e}{\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}} \circ \textcolor{#0087c1}{\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}} = \textcolor{#cc071e}{1} \cdot \textcolor{#0087c1}{1} + \textcolor{#cc071e}{0} \cdot \textcolor{#0087c1}{1} + \textcolor{#cc071e}{(-1)} \cdot \textcolor{#0087c1}{1} = 1 - 1 = 0\]
Somit kann die Gerade \(g\) (echt) parallel zur Ebene verlaufen oder in der Ebene liegen. Deshalb ist noch zu prüfen, ob der Aufpunkt von \(g\) in der Ebene liegt.
Aufpunkt \(\textcolor{#e9b509}{(0|1|1)}\) in die Ebene \(x_1 + x_2 + x_3 = 2\) eingesetzt ergibt:
\[\begin{align*}\textcolor{#e9b509}{0} + \textcolor{#e9b509}{1} + \textcolor{#e9b509}{1} &= 2 \\[0.8em] 2 &= 2 &&(\text{w})\end{align*}\]
Also liegt die Gerade \(g\) in der Ebene.


