Bei einer Routineinspektion wird die Passagierkabine eines zufällig ausgewählten Flugzeugs des Typs X überprüft. Ein Mangel der Beleuchtung sowie ein Mangel der Klimaanlage liegen bei Flugzeugen dieses Typs jeweils mit einer bestimmten Wahrscheinlichkeit vor; diese Wahrscheinlichkeiten können der folgenden Vierfeldertafel entnommen werden.
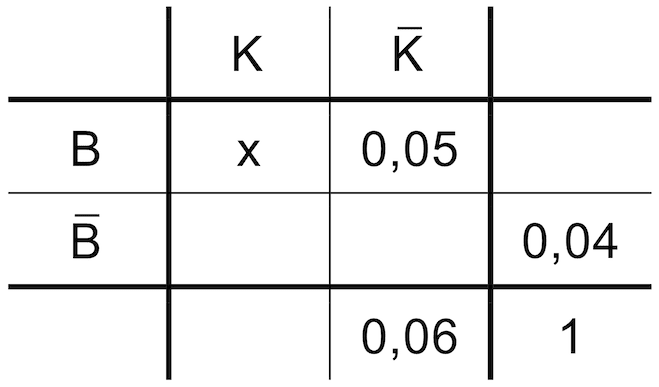
\(B\): Beleuchtung einwandfrei
\(\overline{B}\): Beleuchtung mangelhaft
\(K\): Klimaanlage einwandfrei
\(\overline{K}\): Klimaanlage mangelhaft
Bestimmen Sie den Wert von \(x\) und beschreiben Sie das zugehörige Ereignis in Worten.
(3 BE)
Lösung zu Teilaufgabe 3a
| \(K\) | \(\overline{K}\) | ||
| \(B\) | \(\bf{0{,}91}\) | \(0{,}05\) | \(\bf{0{,}96}\) |
| \(\overline{B}\) | \(\bf{0{,}03}\) | \(\bf{0{,}01}\) | \(0{,}04\) |
| \(\bf{0{,}94}\) | \(0{,}06\) | \(1\) |
\(x = P(B \cap K)\)
Ereignis \(B \cap K\):
"Sowohl die Beleuchtung, als auch die Klimaanlage sind einwandfrei." oder
"Weder die Beleuchtung noch die Klimaanlage sind mangelhaft."
\(x = P(B \cap K)\) bestimmen:
\[P(B) = 1 - P(\overline{B}) = 1 - 0{,}04 = 0{,}96\]
\[P(B \cap K) = P(B) - P(B \cap \overline{K}) = 0{,}96 - 0{,}05 = 0{,}91\]
Vierfeldertafel vervollständigen (Ergänzung):
\[P(K) = 1 - P(\overline{K}) = 1 - 0{,}06 = 0{,}94\]
\[P(\overline{B} \cap \overline{K}) = P(\overline{K}) - P(B \cap \overline{K}) = 0{,}06 - 0{,}05 = 0{,}01\]
\[P(\overline{B} \cap K) = P(\overline{B}) - P(\overline{B} \cap \overline{K}) = 0{,}04 - 0{,}01 = 0{,}03\]
oder
\[P(\overline{B} \cap K) = P(K) - P(B \cap K) = 0{,}94 - 0{,}91 = 0{,}03\]


