Alle Extrempunkte der Graphen der Schar liegen auf einer Gerade. Begründen Sie, dass es sich dabei um die Gerade mit der Gleichung \(y = x\) handelt.
(3 BE)
Lösung zu Teilaufgabe 2f
1. Möglichkeit: Funktion \(f\) aus Aufgabe 1 berücksichtigen
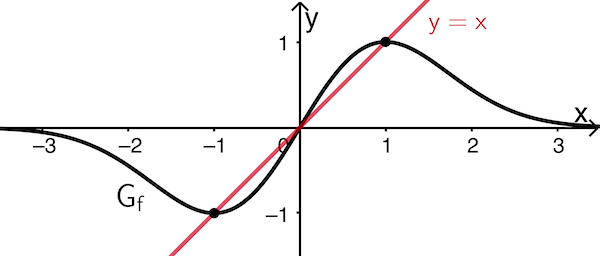
Graph der Funktion \(f\) aus Aufgabe 1, Trägergerade der Extrempunkte mit der Gleichung \(\textcolor{#cc071e}{y = x}\)
\[f_a(x) = x \cdot e^{-\frac{1}{2}a \cdot x^2 + \frac{1}{2}}; \; D_{f_a} = \mathbb R, \; a \in \mathbb R\]
\[f(x) = x \cdot e^{-\frac{1}{2}x^2 + \frac{1}{2}} = f_1(x); \; D_f = \mathbb R\]
Die Funktion \(f\) aus Aufgabe 1 entspricht der Scharfunktion \(f_1\) der Funktionenschar \(f_a\). Aus Teilaufgabe 1c ist bekannt, dass der Graph von \(f\) den Hochpunkt \((1|1)\) bzw. den Tiefpunkt \((-1|-1)\) besitzt. Die Koordinaten der Extrempunkte bestätigen, dass alle Extrempunkte der Funktionenschar \(f_a\) auf der Gerade mit der Gleichung \(\textcolor{#cc071e}{y = x}\) liegen.
Anmerkung:
Wegen der Symmetrie von \(G_f\) bezüglich des Koordinatenursprungs (vgl. Teilaufgabe 1a) genügt es, die Koordinaten des Hoch- oder Tiefpunkts zu betrachten.
2. Möglichkeit: Koordinaten der Extrempunkte von \(f_a\) bestimmen
„Die Extremstellen von \(f_a\) stimmen mit den Lösungen der Gleichung \(a \cdot x^2 = 1\) überein." (vgl. Teilaufgbabe 2e)
Mithilfe dieser Gleichung lassen sich die Koordinaten der Extrempunkte von \(f_a\) in Abhängigkeit des Parameters \(a\) mit \(a > 0\) bestimmen.
\[a \cdot x^2 = 1 \enspace \Leftrightarrow \enspace x^2 = \frac{1}{a} \enspace \Rightarrow \enspace \textcolor{#cc071e}{x_{1,2} = \pm \sqrt{\frac{1}{a}}}\enspace (a > 0)\]
\(y\)-Koordinate eines Extrempunkts berechnen:
\[\begin{align*}f_a\left(\textcolor{#cc071e}{\sqrt{\frac{1}{a}}}\right) &= \textcolor{#cc071e}{\sqrt{\frac{1}{a}}} \cdot e^{-\frac{1}{2}a \cdot \left( \textcolor{#cc071e}{\sqrt{\frac{1}{a}}}\right)^2 + \frac{1}{2}} \\[0.8em] &= \sqrt{\frac{1}{a}} \cdot e^{-\frac{1}{2}a \cdot \frac{1}{a}} + \frac{1}{2} \\[0.8em] &= \sqrt{\frac{1}{a}} \cdot e^0 \\[0.8em] &= \textcolor{#cc071e}{\sqrt{\frac{1}{a}}}\end{align*}\]
\[\Rightarrow \enspace HoP\left( \textcolor{#cc071e}{\sqrt{\frac{1}{a}}} \Bigg| \textcolor{#cc071e}{\sqrt{\frac{1}{a}}} \right)\]
\[\begin{align*}f_a\left(\textcolor{#cc071e}{-\sqrt{\frac{1}{a}}}\right) &= \textcolor{#cc071e}{-\sqrt{\frac{1}{a}}} \cdot e^{-\frac{1}{2}a \cdot \left( \textcolor{#cc071e}{-\sqrt{\frac{1}{a}}}\right)^2 + \frac{1}{2}} \\[0.8em] &= -\sqrt{\frac{1}{a}} \cdot e^{-\frac{1}{2}a \cdot \frac{1}{a}} + \frac{1}{2} \\[0.8em] &= -\sqrt{\frac{1}{a}} \cdot e^0 \\[0.8em] &= \textcolor{#cc071e}{-\sqrt{\frac{1}{a}}}\end{align*}\]
\[\Rightarrow \enspace TiP\left( \textcolor{#cc071e}{-\sqrt{\frac{1}{a}}} \Bigg| \textcolor{#cc071e}{-\sqrt{\frac{1}{a}}} \right)\]
Wie die Koordinaten der Extrempunkte der Graphen von \(f_a\) zeigen, liegen die Extrempunkte auf der Gerade mit der Gleichung \(\textcolor{#cc071e}{y = x}\).
3. Möglichkeit: Gleichung der Ortskurve (Trägergraph) der Extrempunkte bestimmen
Prinzip: Sind \((x(a)|y(a))\) die Koordinaten der Extrempunkte in Abhängigkeit des Parameters \(a\), so wird zunächst die \(x\)-Koordinate nach dem Parameter \(a\) aufgelöst. Eingesetzt in die \(y\)-Koordinate, ergibt sich die Funktionsgleichung des Trägergraphen der Extrempunkte (vgl. Abiturskript - 1.7.6 Ortslinie / Trägergraph einer Kurvenschar).
Den Zusammenhang zwischen der \(x\)-Koordinate der Extrempunkte der Graphen von \(f_a\) und dem Parameter \(a\) liefert die Gleichung aus Teilaufgabe 2e. Die \(y\)-Koordinate der Extrempunkte lässt sich allgemein mit \(y = f_a(x)\) angeben.
\(a \cdot x^2 = 1 \enspace \Leftrightarrow \enspace a = \textcolor{#e9b509}{\dfrac{1}{x^2}}\) (vgl. Teilaufgabe 2e)
Eingesetzt in \(y = f_\textcolor{#e9b509}{a}(x)\) folgt:
\[f_\textcolor{#e9b509}{a}(x) = x \cdot e^{-\frac{1}{2}\textcolor{#e9b509}{a} \cdot x^2 + \frac{1}{2}}\]
\[\textcolor{#cc071e}{y} = f_{\textcolor{#e9b509}{\frac{1}{x^2}}}(x) = x \cdot e^{-\frac{1}{2} \cdot \textcolor{#e9b509}{\frac{1}{x^2}} \cdot x^2 + \frac{1}{2}} = x \cdot e^0 \textcolor{#cc071e}{= x}\]
Somit liegen alle Extrempunkte der Graphen der Funktionenschar \(f_a\) auf der Gerade mit der Gleichung \(\textcolor{#cc071e}{y = x}\).


