Nachdem die Verfilmung eines bekannten Romans erfolgreich in den Kinos gezeigt wurde, veröffentlicht eine Tageszeitung das Ergebnis einer repräsentativen Umfrage unter Jugendlichen. Der Umfrage zufolge hatten 88 % der befragten Jugendlichen den Roman zum Zeitpunkt des Kinostarts noch nicht gelesen, 18 % sahen die Verfilmung. Von den Befragten, die laut Umfrage den Roman zum Zeitpunkt des Kinostrats bereits gelesen hatten, gaben 60 % an, die Verfilmung gesehen zu haben.
Betrachtet werden folgende Ereignisse:
\(R\,\): "Eine aus den Befragten zufällig ausgewählte Person hatte laut Umfrage den Roman zum Zeitpunkt des Kinostarts bereits gelesen."
\(V\,\): "Eine aus den Befragten zufällig ausgewählte Person sah laut Umfrage die Verfilmung."
Bestimmen Sie die Wahrscheinlichkeit dafür, dass eine aus den Befragten zufällig ausgewählte Person, die laut Umfrage den Roman zum Zeitpunkt des Kinostarts noch nicht gelesen hatte, angab, die Verfilmung gesehen zu haben.
(5 BE)
Lösung zu Teilaufgabe 1a
Analyse der Angabe:
"... hatten 88 % .. den Roman ... noch nicht gelesen, ..."
\(P(\overline{R}) = 0{,}88\)
"... 18 % sahen die Verfilmung."
\(P(V) = 0{,}18\)
"Von den Befragten, die ... den Roman ... gelesen hatten, gaben 60 % an, die Verfilmung gesehen zu haben."
\(P_R(V) = 0{,}6\)
Gesucht ist die bedingte Wahrscheinlichkeit \(P_{\overline{R}}(V)\)
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[P_{\overline{R}}(V) = \frac{P(\overline{R} \cap V)}{P(\overline{R})}\]
1. Lösungsansatz: Baumdiagramm
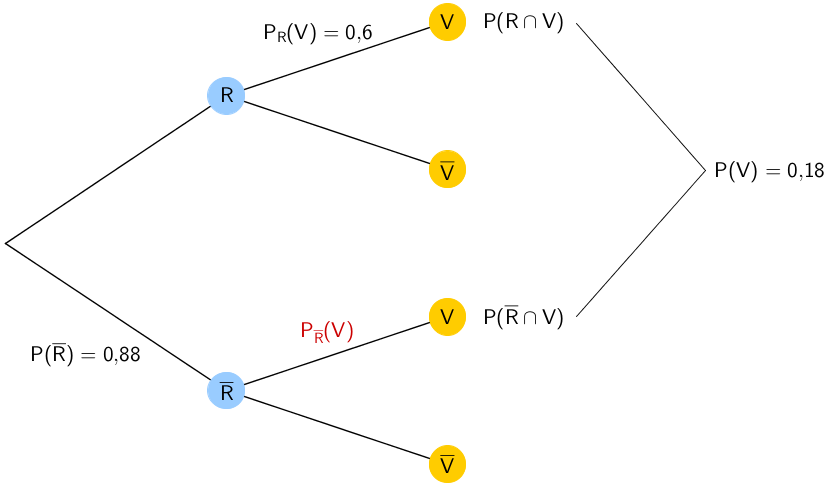
Gegebene Wahrscheinlichkeiten \(\,P(\overline{R})\,\), \(\,P(V)\,\) und \(\,P_R(V)\,\) sowie gesuchte bedingte Wahrscheinlichkeit \(\,P_{\overline{R}}(V)\)
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Knotenregel anwenden:
\[P(R) = 1 - P(\overline{R}) = 1 - 0{,}88 = 0{,}12\]
1.Pfadregel anwenden:
\[P(R \cap V) = P(R) \cdot P_R(V) = 0{,}12 \cdot 0{,}6 = 0{,}072\]
2. Pfadregel anwenden:
\[\begin{align*} P(V) &= P(R \cap V) + P(\overline{R} \cap V) \\[0.8em] \Longleftrightarrow \quad P(\overline{R} \cap V) &= P(V) - P(R \cap V) \\[0.8em] &= 0{,}18 - 0{,}072 \\[0.8em] &= 0{,}108 \end{align*}\]
Bedingte Wahrscheinlichkeit \(P_{\overline{R}}(V)\) berechnen:
\[P_{\overline{R}}(V) = \frac{P(\overline{R} \cap V)}{P(\overline{R})} = \frac{0{,}108}{0{,}88} \approx 0{,}123 = 12{,}3\,\%\]
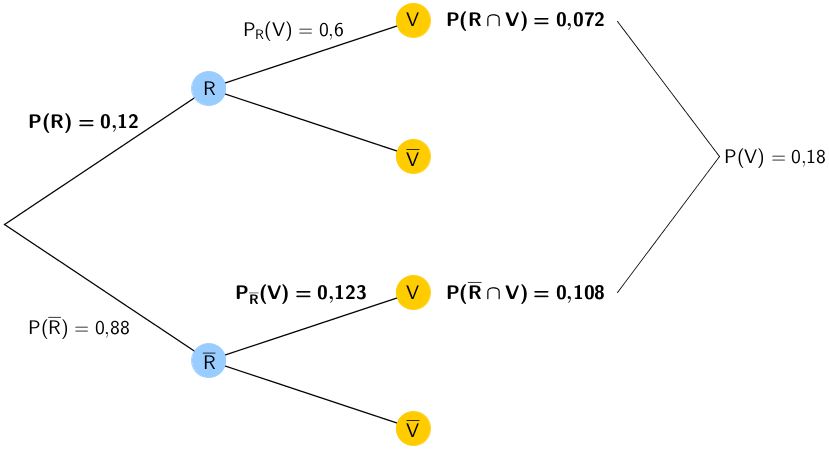
Errechnete Wahrscheinlichkeiten \(\,P(R)\,\), \(\,P(R \cap V)\,\) und \(\,P(\overline{R} \cap V)\,\) der Zwischenschritte und Ergebnis der gesuchten bedingten Wahscheinlichkeit \(\,P_{\overline{R}}(V)\)
2. Lösungsansatz: Vierfeldertafel
Gegeben: \(\;P(\overline{R}) = 0{,}88\,\), \(\enspace P(V) = 0{,}18\,\), \( \enspace P_R(V) = 0{,}6\)
| \(V\) | \(\overline V\) | ||
| \(R\) | |||
| \(\overline{R}\) | \(0{,}88\) | ||
| \(0{,}18\) | \(1\) |
\[P(R) = 1 - P(\overline{R}) = 1 - 0{,}88 = 0{,}12\]
| \(V\) | \(\overline V\) | ||
| \(R\) | \(\bf{0{,}12}\) | ||
| \(\overline{R}\) | \(0{,}88\) | ||
| \(0{,}18\) | \(1\) |
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[\begin{align*}P_R(V) &= \frac{P(R \cap V)}{P(R)} \\[0.8em] \Longleftrightarrow \quad P(R \cap V) &= P_R(V) \cdot P(V) \\[0.8em] &= 0{,}6 \cdot 0{,}12 \\[0.8em] &= 0{,}072\end{align*}\]
| \(V\) | \(\overline V\) | ||
| \(R\) | \(\bf{0{,}072}\) | \(\bf{0{,}12}\) | |
| \(\overline{R}\) | \(0{,}88\) | ||
| \(0{,}18\) | \(1\) |
\[\begin{align*} P(\overline{R} \cap V) &= P(V) - P(R \cap V) \\[0.8em] &= 0{,}18 - 0{,}072 \\[0.8em] &= 0{,}108 \end{align*}\]
| \(V\) | \(\overline V\) | ||
| \(R\) | \(\bf{0{,}072}\) | \(\bf{0{,}12}\) | |
| \(\overline{R}\) | \(\bf{0{,}108}\) | \(0{,}88\) | |
| \(0{,}18\) | \(1\) |
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[P_{\overline{R}}(V) = \frac{P(\overline{R} \cap V)}{P(\overline{R})} = \frac{0{,}108}{0{,}88} \approx 0{,}123 = 12{,}3\,\%\]


