Um den Flächeninhalt der Vorderseite der Dachgaube zu ermitteln, wird eine Stammfunktion \(F\) von \(f\) betrachtet.
Einer der Graphen I, II und III ist der Graph von \(F\). Begründen Sie, dass dies Graph I ist, indem Sie jeweils einen Grund dafür angeben, dass Graph II und Graph III nicht infrage kommen.
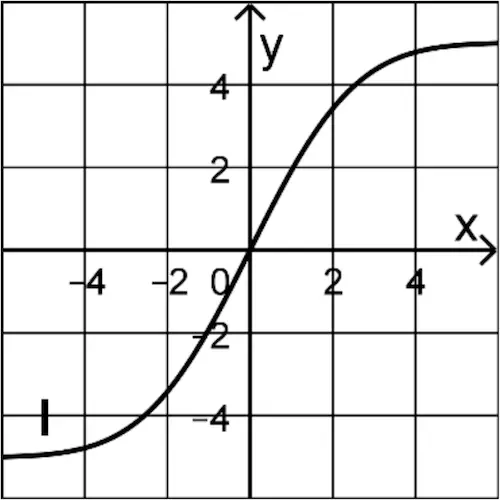
(2 BE)
Lösung zu Teilaufgabe 2c
Mögliche Begründungen:
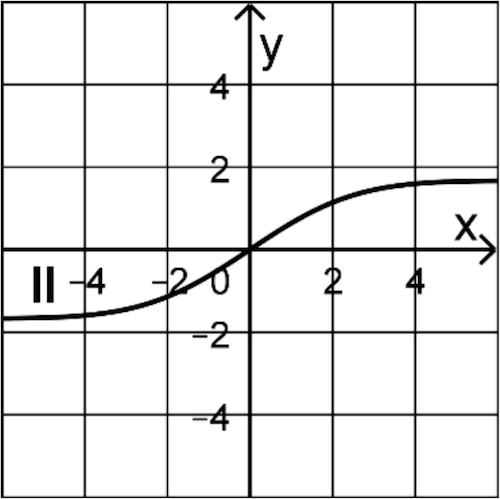
Graph II kommt nicht infrage, da seine Steigung (Steigung der Wendetangente) an der Stelle \(x = 0\) kleiner als \(F'(0) = f(0) = 2\) ist (vgl. Teilaufgabe 1a).
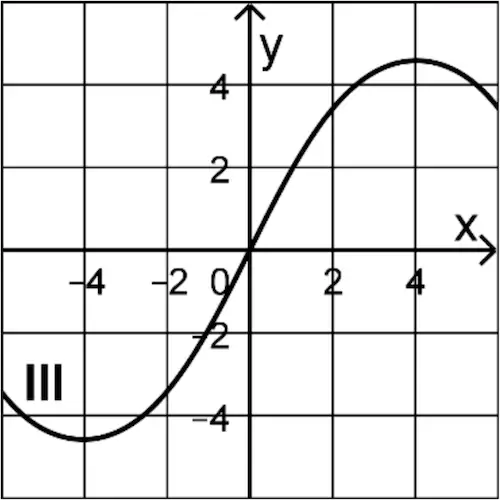
Graph III kommt nicht infrage, da dieser in Bereichen streng monoton fallend ist. Wegen \(F'(x) = f(x) = 2e^{-\frac{1}{8}x^2} > 0\) (Weil \(G_f\) vollständig oberhalb der \(x\)-Achse verläuft) ist der Graph von \(F\) streng monoton steigend.
Somit ist Graph I der Graph von \(F\).
Ausführliche Erklärung (nicht verlangt)
Der Graph der Funktion \(f\) (vgl. Abbildung 1) ist der Graph der ersten Ableitungsfunktion einer Stammfunktion \(F\) von \(f\). Es gilt:
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
\[F'(x) = f(x)\]
Begründung, weshalb Graph II nicht infrage kommt
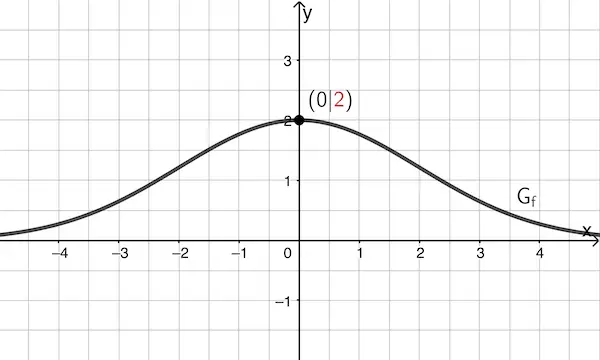Abb. 1
Der Graph der Funktion \(f\) schneidet die \(y\)-Achse im Punkt \((0|\textcolor{#cc071e}{2})\). Damit gilt \(f(0) = \textcolor{#cc071e}{F'(0) = 2}\). Das bedeutet, dass der Graph einer Stammfunktion \(F\) an der Stelle \(x = 0\) die Steigung 2 hat.
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
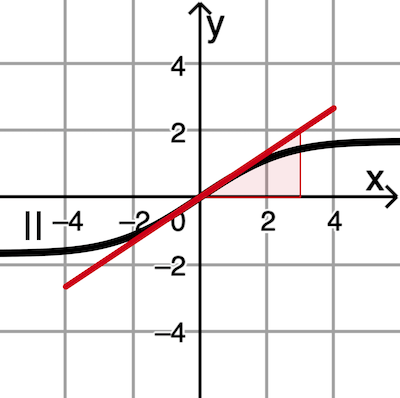
Graph II zeigt an der Stelle \(x = 0\) in etwa die Steigung \(\textcolor{#cc071e}{\dfrac{2}{3}}\), also deutlich kleiner als 2, und kommt deshalb nicht als Graph einer Stammfunktion \(F\) von \(f\) infrage.
Begründung, weshalb Graph III nicht infrage kommt
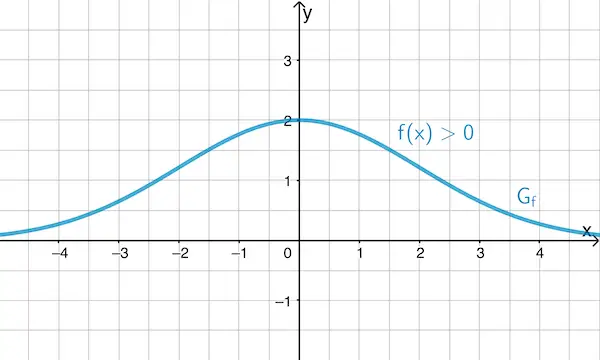Abb. 1
Für alle \(x \in \mathbb R\) gilt \(\textcolor{#0087c1}{F'(x) = f(x)} = 2e^{-\frac{1}{8}x^2} \textcolor{#0087c1}{> 0}\). Abbildung 1 bestätigt dies, denn der Graph von \(\textcolor{#0087c1}{f}\) verläuft vollständig oberhalb der \(\textcolor{#0087c1}{x}\)-Achse.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(f'(x) < 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) fällt streng monoton in \(I\)
\(f'(x) > 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Nach dem Monotoniekriterium folgt aus \(\textcolor{#0087c1}{F'(x) > 0}\) für \(x \in \mathbb R\), dass der Graph einer Stammfunktion \(F\) von \(f\) über seinem gesamten Verlauf streng monoton steigend ist.
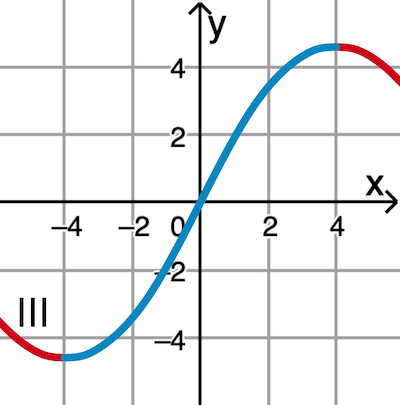
Graph III weist Bereiche auf, in denen dieser streng monoton fallend ist und kommt deshalb nicht als Graph einer Stammfunktion \(F\) von \(f\) infrage.
