Berechnen Sie, um wie viel Prozent der Inhalt der Querschnittsfläche des Tunnels bei einer Modellierung mit \(f\) von dem in Aufgabe 2a berechneten Wert abweicht.
(2 BE)
Lösung zu Teilaufgabe 3c
Geometrische Berechnung eines Funktionswerts einer Integralfunktion, Prozentuale Abweichung
\(\displaystyle k(x) = 5 \cdot \cos\left( \frac{\pi}{10} \right); \; D_{k} = [-5;5]\) (vgl. Teilaufgabe 2a)
\(f(x) = \sqrt{25 - x^{2}}; \; D_{f} = [-5;5]\) (vgl. Teilaufgabe 3a)
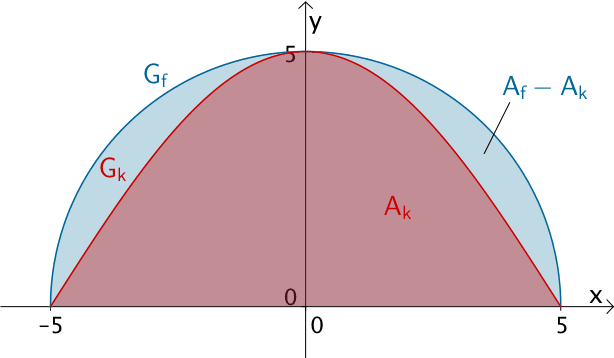
Flächeninhalt \(A_{k}\) der Querschnittsffläche des Tunnels bei einer Modellierung mit der Funktion \(k \colon x \mapsto 5 \cdot \cos\left( \frac{\pi}{10} \cdot x \right); \; D_{k} = [-5;5]\) (vgl. Teilaufgabe 2a)
Abweichung \(A_{f} - A_{k}\) des Flächeninhalts \(A_{f}\) der Querschnittsfläche des Tunnels bei einer Modellierung mit der Funktion \(f \colon x \mapsto \sqrt{25 - x^{2}}; \; D_{f} = [-5;5]\) vom Flächeninhalt \(A_{k}\)
Prozentuale Abweichung des Flächeninhalts \(A_{f}\) der Querschnittfläche des Tunnels bei einer Modellierung mit \(f\) vom Flächeninhalt \(A_{k}\) der Querschnittfläche des Tunnels bei einer Modellierung mit \(k\):
\[\frac{A_{f} - A_{k}}{A_{k}} \cdot 100\,\%\]
Aus Teilaufgabe 2a ist der Inhalt der Querschnittsfläche des Tunnels bei einer Modellierung mit \(k\) bereits bekannt.
\[A_{k} = \frac{100}{\pi} \, \text{m}^{2}\]
Flächeninhalt \(A_{f}\) berechnen:
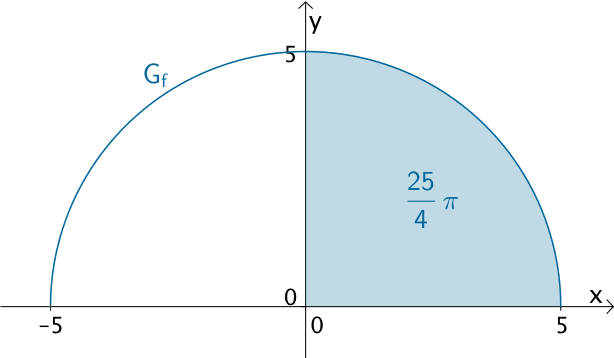
Aus Teilaufgabe 3b ist bekannt, dass \(\displaystyle F(5) = \int_{0}^{5} f(t)\, dt = \frac{25}{4}\pi\) gilt, und dass dieser Wert gleich der Maßzahl des Flächeninhalts des Viertelkreises ist, den der Graph der Funktion \(f\) im I. Quadranten mit den Koordinatenachsen einschließt.
Damit lässt sich der Flächeninhalt \(A_{f}\) der Querschnittfläche des Tunnels bei einer Modellierung mit \(f\) berechnen. Er entspricht dem Flächeninhalt des Halbkreises, den der Graph der Funktion \(f\) mit der \(x\)-Achse einschließt in Quadratmetern.
\[\begin{align*}A_{f} &= \left(\int_{-5}^{5} f(t)\, dt\right)\text{m}^{2} \\[0.8em] &= \left(2 \cdot \int_{0}^{5} f(t)\, dt\right)\text{m}^{2} \\[0.8em] &= \left(2 \cdot \frac{25}{4}\pi\right)\text{m}^{2} \\[0.8em] &= \frac{25}{2}\pi\,\text{m}^{2}\end{align*}\]
Der Inhalt der Querschnittsfläche des Tunnels bei einer Modellierung mit \(f\) beträgt \(\frac{25}{2}\pi\,\sf{m}^{2}\).
Prozentuale Abweichung berechnen:
\[A_{k} = \frac{100}{\pi}\,\text{m}^{2}; \enspace A_{f} = \frac{25}{2}\pi\,\text{m}^{2}\]
\[\frac{A_{f} - A_{k}}{A_{k}} \cdot 100\,\% = \frac{\left(\frac{25}{2}\pi - \frac{100}{\pi}\right)\text{m}^{2}}{\frac{100}{\pi}\,\text{m}^{2}} \cdot 100\,\% \approx 23{,}4\,\%\]
Der Inhalt der Querschnittfläche des Tunnels bei einer Modellierung mit \(f\) weicht um ca. 23,4 % vom Inhalt der Querschnittfläche des Tunnels bei einer Modellierung mit \(k\) ab.

