Geben Sie den Term einer in \(\mathbb R\) definierten Funktion an, deren Graph im Punkt \((2|1)\) eine waagrechte Tangente, aber keinen Extrempunkt hat.
(3 BE)
Lösung zu Teilaufgabe 2
In einem Extrem- oder Terrassenpunkt des Graphen einer Funktion hat der Graph eine waagrechte Tangente. Gesucht ist also der Term einer in \(\mathbb R\) definierten Funktion, deren Graph den Terrassenpunkt \((2|1)\) besitzt.
Beispielsweise hat der Graph der in \(\mathbb R\) definierten Potenzfunktion \(x \mapsto x^{3}\) den Terrassenpunkt \((0|0)\).
Dann besitzt der um 2 LE in Richtung der positiven \(x\)-Achse und um 1 LE in Richtung der positiven \(y\)-Achse verschobene Graph den Terrassenpunkt \((2|1)\).
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[\Longrightarrow \quad (x - 2)^{3} + 1\]
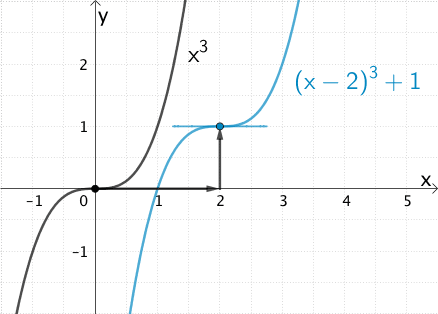
Entstehung des Graphen der Funktion \(x \mapsto (x - 2)^{3} + 1\) mit dem Terrassenpunkt \((2|1)\) aus dem Graphen der Potenzfunktion \(x \mapsto x^{3}\) mit dem Terrassenpunkt \((0|0)\)

