Gegeben ist die gebrochenrationale Funktion \(f \colon x \mapsto \dfrac{6 - x^{2}}{x^{2} - 9}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Bestimmen Sie die maximale Definitionsmenge \(D_{f}\) der Funktion \(f\).
b) Berechnen Sie die Schnittpunkte von \(G_{f}\) mit den Koordinatenachsen.
c) Untersuchen Sie das Symmetrieverhalten von \(G_{f}\).
d) Untersuchen Sie das Verhalten von \(f\) an den Rändern von \(D_{f}\).
e) Geben Sie die Gleichungen aller Asymptoten von \(G_{f}\) an.
f) Skizzieren Sie \(G_{f}\) unter Berücksichtigung der bisherigen Ergebnisse in ein geeignetes Koordinatensystem.
\[f(x) = \frac{6 - x^{2}}{x^{2} - 9}\]
a) Maximale Definitionsmenge \(D_{f}\) der Funktion \(f\)
Da die Division durch Null in der Mathematik nicht erlaubt ist, ist eine gebrochenrationale Funktion an den Nullstellen des Nennerterms nicht definiert.
\[\begin{align*} x^{2} - 9 &= 0 &&| + 9 \\[0.8em] x^{2} &= 9 &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm 3 \end{align*}\]
oder
\[\begin{align*} \underbrace{x^{2} - 9}_{\large{a^{2} \, - \, b^{2}}} &= 0 & &| \; \text{3. Binomische Formel anwenden} \\[0.8em] \underbrace{(x - 3 (x + 3)}_{\large{(a\,-\,b)(a\,+\,b)}} &= 0 \end{align*}\]
\[\Longrightarrow \quad x_{1} = -3; x_{2} = 3\]
An den Nennernullstellen \(x_{1} = -3\) und \(x_{2} = 3\) ist die gebrochenrationale Funktion \(f\) nicht definiert.
\[\Longrightarrow \quad D_{f} = \mathbb R \backslash \{-3;3\}\]
b) Schnittpunkte von \(G_{f}\) mit den Koordinatenachsen
\[f(x) = \frac{6 - x^{2}}{x^{2} - 9}; \; D_{f} = \mathbb R \backslash \{-3;3\}\]
Schnittpunkte von \(G_{f}\) mit der \(x\)-Achse (Nullstellen):
Ein Bruchterm ist gleich Null, wenn der Zählerterm gleich Null ist.
\[\begin{align*}f(x) = 0 \quad \Longrightarrow \quad 6 - x^{2} &= 0 & &| + x^{2} \\[0.8em] 6 &= x^{2} & &| \; \sqrt{\quad} \\[0.8em] \pm \sqrt{6} &= x_{1,2}\end{align*}\]
\[\Longrightarrow \quad N_{1}(-\sqrt{6}|0); \; N_{2}(\sqrt{6}|0)\]
Schnittpunkt von \(G_{f}\) mit der \(y\)-Achse:
Der Schnittpunkt \(S_{y}\) von \(G_{f}\) mit der \(y\)-Achse hat die Koordinaten \(S_{y}(0|f(0))\). Es ist also der Funktionswert \(f(0)\) zu berechnen.
\[f(0) = \frac{6 - 0^{2}}{0^{2} - 9} = -\frac{6}{9} = -\frac{2}{3}\]
\[\Longrightarrow \quad S_{y}\left(0\big|\textstyle -\frac{2}{3}\right)\]
c) Untersuchung des Symmetrieverhaltens von \(G_{f}\)
Man bestimmt den Funktionsterm \(f(-x)\). Gilt \(f(-x) = f(x)\), ist \(G_{f}\) achsensymmetrisch zur \(y\)-Achse. Gilt \(f(-x) = -f(x)\), ist \(G_{f}\) punktsymmetrisch zum Koordinatenursprung \(O(0|0)\). Trifft keiner der beiden Fälle zu, weist \(G_{f}\) keines der beiden Symmetrieverhalten auf.
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
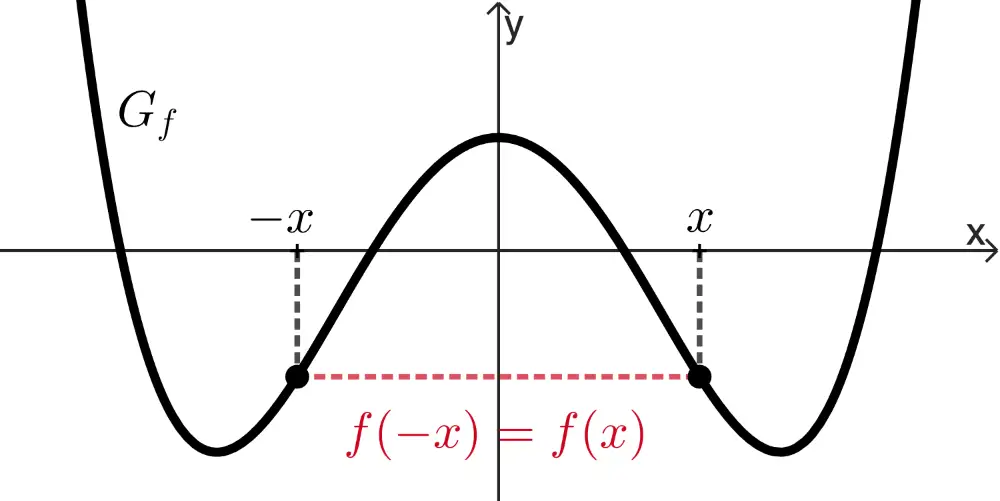
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
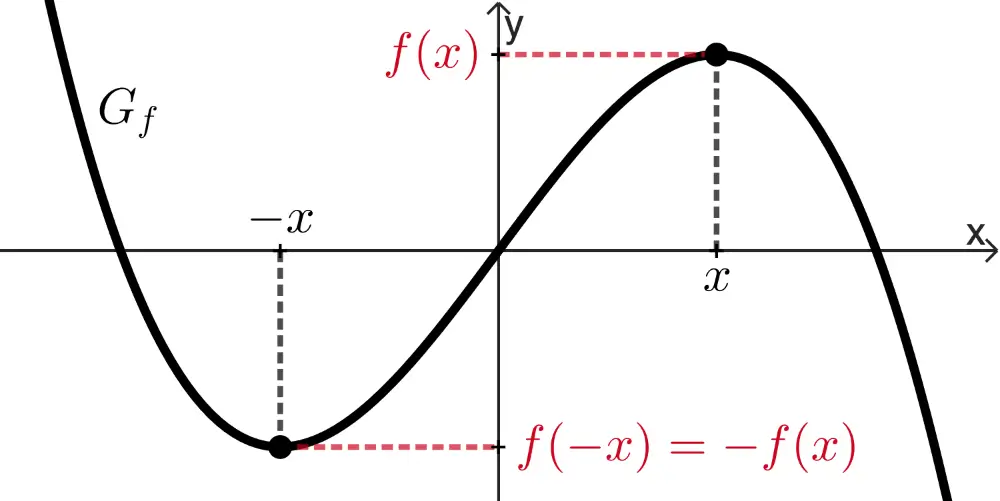
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(x) = \frac{6 - x^{2}}{x^{2} - 9}; \; D_{f} = \mathbb R \backslash \{-3;3\}\]
\[f(-x) = \frac{6 - (-x)^{2}}{(-x)^{2} - 9} = \frac{6 - x^{2}}{x^{2} - 9} = f(x)\]
\(\Longrightarrow \quad G_{f}\) ist achsensymmetrisch zur \(y\)-Achse.
d) Verhalten von \(f\) an den Rändern von \(D_{f}\)
Formuliert man die die maximale Definitionsmenge \(D_{f}\) der Funktion \(f\) in der Intervallschreibweise, sind die Ränder von \(D_{f}\) besser zu erkennen.
\[D_{f} = \mathbb R \backslash \{-3;3\} = \; ]-\infty;-3[ \; \cup \; ]-3;3[ \; \cup \; ]3;+\infty[\]
Es ist demnach das Verhalten der Funktion \(f\) für \(x \to -\infty\), \(x \to -3^{-}\), \(x \to - 3^{+}\), \(x \to 3^{-}\), \(x \to 3^{+}\) und \(x \to +\infty\) zu untersuchen.
Vorab der Grezwertbetrachtungen erfolgt noch eine Bewertung der Art der in Teilaufgabe a festgestellten Definitionslücken \(x = -3\) und \(x = 3\) (Nennernullstellen).
Da die Nennernullstellen von \(f\) nicht zugleich Nullstellen des Zählers sind (vgl. Teilaufgabe b), sind die Definitionslücken \(x = -3\) und \(x = 3\) nicht hebbar. Folglich sind \(x = -3\) und \(x = 3\) Polstellen der Funktion \(f\). Die einfachen Nennernullstellen lassen auf Polstellen mit Vorzeichenwechsel schließen.
Am vollständig faktorisierten Funkktionsterm \(f(x)\) - beispielsweise mithilfe der 3. Binomischen Formel - ist die Art der Definitionslücken gut erkennen:
\[\begin{align*}f(x) &= \frac{\overbrace{6 - x^{2}}^{\large{a^{2}\,-\,b^{2}}}}{\underbrace{x^{2} - 9}_{\large{a^{2}\,-\,b^{2}}}} & &| \; \text{3. Binomische Formel anwenden} \\[0.8em] &= \frac{\overbrace{(\sqrt{6} - x)(\sqrt{6} + x)}^{\large{(a\,-\,b)(a\,+\,b)}}}{\underbrace{(x - 3)(x + 3)}_{\large{(a\,-\,b)(a\,+\,b)}}}\end{align*}\]
\(\Longrightarrow \quad\) einfache Nennernullstellen \(\neq\) Zählernullstellen
\(\Longrightarrow \quad\) Polstellen \(x = -3\) und \(x = 3\) mit Vorzeichenwechsel
Anmerkung
Eine hebbare Definitionslücke einer gebrochenrationalen Funktion liegt immer dann vor, wenn eine Nennernullstelle zugleich Zählernullstelle ist und der Funktionsterm so gekürzt werden kann, dass keine Nennernullstelle mehr existiert. Der Graph der gebrochenrationalen Funktion zeigt dann an der entsprechenden Stelle ein Definitionsloch, während er in der Umgebung einer Polstelle gegen \(- \infty\) bzw. \(+ \infty\) strebt.
Um das Verhalten von \(f\) an den Rändern von \(D_{f}\) zu untersuchen, sind also insgesamt folgende Grenzwertbetrachtungen zu berücksichtigen:
\(\lim \limits_{x \; \to \, {-3}^{-}} f(x)\) und \(\lim \limits_{x \, \to \, {-3}^{+}} f(x)\)
bzw.
\(\lim \limits_{x\, \to \, 3^{-}} f(x)\) und \(\lim \limits_{x \, \to \, 3^{+}} f(x)\)
sowie
\(\lim \limits_{x \, \to \, -\infty} f(x)\) und \(\lim \limits_{x \, \to \, +\infty} f(x)\)
Es ist sinnvoll die in Teilaufgabe c festgestellte Achsensymmetrie von \(G_{f}\) bzgl. der \(y\)-Achse zu berücksichtigen.
\[\lim \limits_{x\,\to\,{-3}^{-}} f(x) = \lim \limits_{x\,\to\,{-3}^{-}} \frac{\overbrace{6 - x^{2}}^{\large{\to\,-3}}}{\underbrace{\underbrace{(x - 3)}_{\large{\to\,-6}}\underbrace{(x + 3)}_{\large{\to\,0^{-}}}}_{\large{\to\,0^{+}}}} = -\infty\]
\[\lim \limits_{x\,\to\,{-3}^{+}} f(x) = \lim \limits_{x\,\to\,{-3}^{+}} \frac{\overbrace{6 - x^{2}}^{\large{\to\,-3}}}{\underbrace{\underbrace{(x - 3)}_{\large{\to\,-6}}\underbrace{(x + 3)}_{\large{\to\,0^{+}}}}_{\large{\to\,0^{-}}}} = +\infty\]
Aufgrund der Achsensymmetrie von \(G_{f}\) bzgl. der \(y\)-Achse folgt:
\[\lim \limits_{x \, \to \, 3^{-}} f(x) = \lim \limits_{x \,\to\,3^{-}} = +\infty \]
\[\lim \limits_{x \, \to \, 3^{+}} f(x) = \lim \limits_{x \,\to\,3^{+}} = -\infty \]
Verhalten von \(G_{f}\) im Unendlichen:
Wegen der Achsensymmetrie von \(G_{f}\) bzgl. der \(y\)-Achse müssen die Grenzwertbetrachtungen \(x \to -\infty\) und \(x \to +\infty\) das gleiche Grenzwertverhalten ergeben. Die Grenzwertbetrachtungen können daher zu einer Grenzwertbetrachtung \(x \to \pm\infty\) zusammengefasst werden.
\[f(x) = \frac{6 - x^{2}}{x^{2} - 9}; \; D_{f} = \mathbb R \backslash \{-3;3\}\]
Für eine aussagekräftige Grenzwertbetrachtung \(\lim \limits_{x \, \to \, \pm \infty} f(x)\) wird die höchste Potenz des Nennerpolynoms von \(f\) im Nenner und im Zähler ausgeklammert.
\[\begin{align*}\lim \limits_{x\,\to\,\pm\infty} f(x) &= \lim \limits_{x\,\to\,\pm\infty} \frac{6 - x^{2}}{x^{2}-9} \\[0.8em] &= \frac{\cancel{x^{2}} \cdot \Big( \overbrace{\frac{6}{x^{2}}}^{\large{\to\,0}} - 1 \Big)}{\cancel{x^{2}} \cdot \Big( 1 - \underbrace{\frac{9}{x^{2}}}_{\large{\to\,0}} \Big)} \\[0.8em] &= -1 \end{align*}\]
e) Gleichungen aller Asymptoten von \(G_{f}\)
Die Gleichungen der senkrechten Asymptoten ergeben sich unmittelbar anhand der Polstellen \(x = -3\) und \(x = 3\).
Der Graph der Funktion \(f\) besitzt zwei senkrechte Asymptoten mit den Gleichungen \(x = -3\) und \(x = 3\).
Die Gleichung der waagrechten Asymptote kann der Grenzwertbetrachtung \(\lim \limits_{x\,\to\,\pm\infty} f(x) = -1\) entnommen werden (vgl. Teilaufgabe d).
Der Graph der Funktion \(f\) besitzt die waagrechte Asymptote mit der Gleichung \(y = -1\).
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
Als Alternative lässt sich die waagrechte Asymptote anhand der Grade des Zähler- und des Nennerpolynoms ermitteln. Die gebrochenrationale Funktion \(f \colon x \mapsto \dfrac{6 - x^{2}}{x^{2} - 9}\) besitzt im Zähler und Im Nenner ein Polynom 2. Grades (quadratischer Term). Daraus lässt sich schlussfolgern, dass eine waagrechte Asymptote parallel zur \(x\)-Achse das Verhalten von \(G_{f}\) im Unendlichen bestimmt. Die Gleichung der waagrechten Asymptote ergibt sich dann mithilfe des Quotienten der Koeffizienten der höchsten Potenzen (Faktoren der Potenzen) des Zähler- und im Nennerpolynoms.
\[f(x) = \frac{6 - x^{2}}{x^{2} - 9} = \frac{6 + (-1) \cdot x^{2}}{(+1) \cdot x^{2} - 9}\]
Im Zähler der gebrochenrationalen Funktion \(f\) besitzt die die höchste Potenz \(x^{2}\) den Koeffizienten \(-1\) und im Nenner besitzt die höchste Potenz \(x^{2}\) den Koeffizienten \(+1\).
\(\Longrightarrow \quad\)waagrechte Asymptote \(y = \dfrac{-1}{+1} = -1\)
f) Skizzieren von \(G_{f}\) unter Berücksichtigung der bisherigen Ergebnisse
Bisherige Ergebnisse:
- \(D_{f} = \mathbb R \backslash \{-3;3\}\)
- Schnittpunkte von \(G_{f}\) mit der \(x\)-Achse: \(N_{1}(-\sqrt{6}|0); \; N_{2}(\sqrt{6}|0)\)
- Schnittpunkt von \(G_{f}\) mit der \(y\)-Achse: \(S_{y}\left(0\big|\textstyle -\frac{2}{3}\right)\)
- \(G_{f}\) ist achsensymmetrisch zur \(y\)-Achse.
- \(\lim \limits_{x\,\to\,{-3}^{-}} f(x) = -\infty; \; \lim \limits_{x\,\to\,{-3}^{+}} f(x) = +\infty;\)
- \(\lim \limits_{x\,\to\,3^{-}} f(x) = +\infty; \; \lim \limits_{x\,\to\,3^{+}} f(x) = -\infty;\)
- \(\lim \limits_{x\,\to\,\pm\infty} f(x) = -1\)
- Senkrechte Asymptoten: \(x = -3\) und \(x = 3\)
- Waagrechte Asymptote: \(y = -1\)
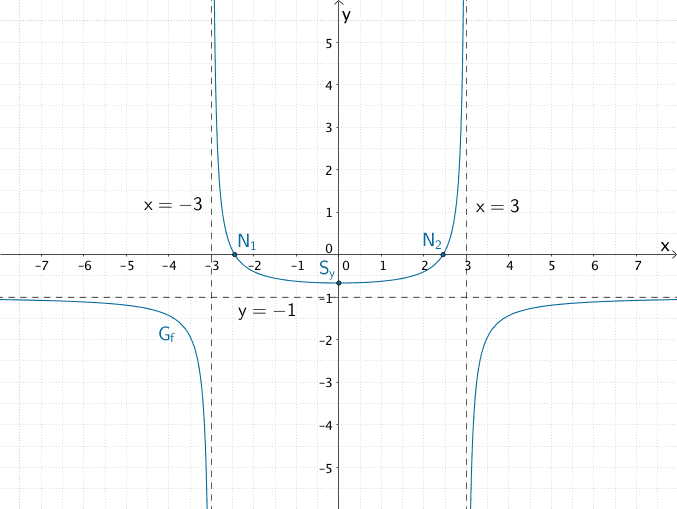
Graph der gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{6 - x^{2}}{x^{2} - 9}\) mit der maximalen Definitionsmenge \(D_{f} = \mathbb R \backslash \{-3;3\}\)

