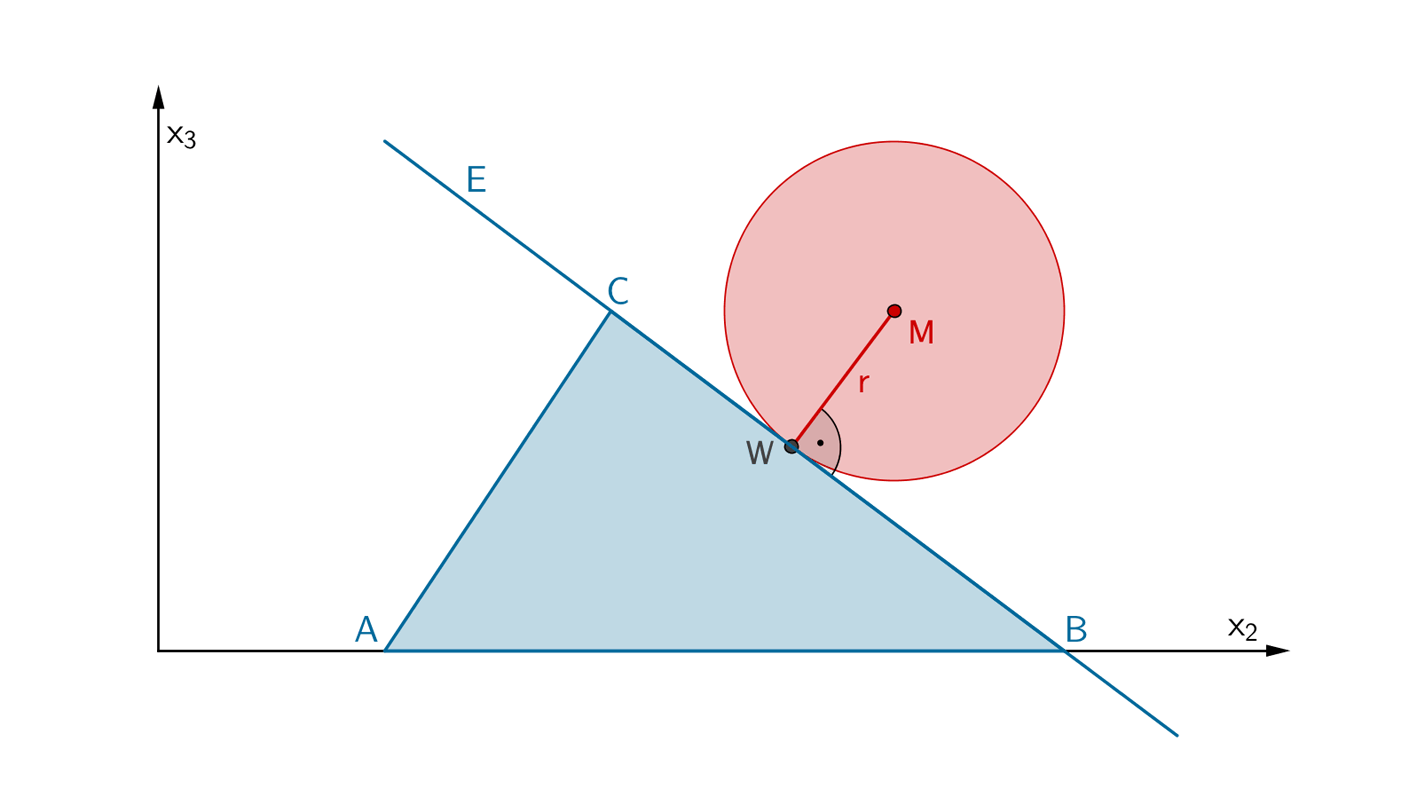
Das Prisma ist das Modell eines Holzkörpers, der auf einer durch die \(x_1x_2\)-Ebene beschriebenen horizontalen Fläche liegt. Der Punkt \(M\,(5|6{,}5|3)\) ist Mittelpunkt einer Kugel, die die Seitenfläche \(BSTC\) im Punkt \(W\) berührt.
Berechnen Sie den Radius \(r\) der Kugel sowie die Koordinaten von \(W\,\).
(Teilergebnis: \(r = 1{,}5\))
(6 BE)
Lösung zu Teilaufgabe f
Der Punkt \(W\) ist der Lotfußpunkt des Lotes des Mittelpunktes \(M\) auf die Seitenfläche \(BSTC\). Die Seitenfläche \(BSTC\) liegt in der Ebene \(E\) (siehe Teilaufgabe b). Der Radius \(r\) der Kugel ist gleich der Länge der Strecke \([MW]\) bzw. gleich dem Abstand \(d\,(M;E)\) des Mittelpunktes \(M\) von der Ebene \(E\,\).
1.Lösungsansatz: Lotfußpunkt \(W\,\), Länge der Strecke \([MW]\)
Koordinaten des Punktes \(W\)
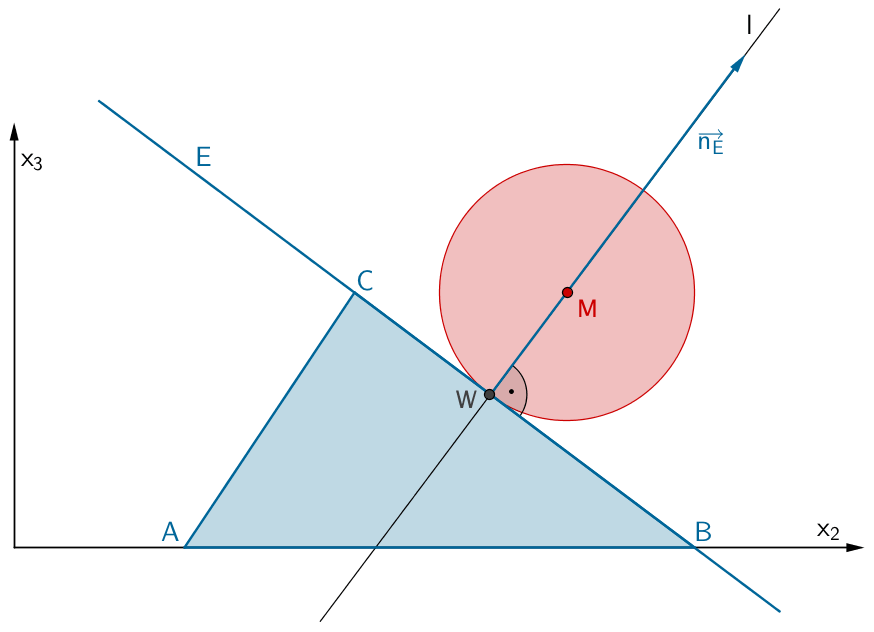
Die Lotgerade \(\,l\,\) mit \(\,M \in l\,\) schneidet die Ebene \(\,E\,\) im Lotfußpunkt \(\,W\,\).
Lotgerade \(l\) mit \(M \in l\) auf die Ebene \(E\) bestimmen:
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\[M\,(5|6{,}5|3)\,, \quad \overrightarrow{n}_E = \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\]
\[\begin{align*} l\,\colon \enspace \overrightarrow{X} &= \overrightarrow{M} + \lambda \cdot \overrightarrow{n}_E \\[0.8em] \overrightarrow{X} &= \begin{pmatrix} 5 \\ 6{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\,, \quad \lambda \in \mathbb R \end{align*}\]
Lotfußpunkt \(W\) berechnen:
Zur Berechnung des Lotfußpunktes \(W\) setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) aus der Geradengleichung von \(l\) in die Normalengleichung der Ebene \(E\) ein und löst die Gleichung nach dem Parameter \(\lambda\) auf.
\[l\,\colon \enspace \overrightarrow{X} = \begin{pmatrix} 5 \\ 6{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\]
\(E\,\colon \enspace 3x_2 + 4x_3 -24 = 0\;\) (siehe Teilaufgabe b)
\[\begin{align*} l \cap E\,\colon \enspace 3 \cdot (6{,}5 + 3\lambda) + 4 \cdot (3 + 4\lambda) - 24 &= 0 \\[0.8em] 19{,}5 + 9\lambda + 12 + 16\lambda - 24 &= 0 \\[0.8em] 25\lambda + 7{,}5 &= 0 & &| -7{,}5 \\[0.8em] 25\lambda &= -7{,}5 & &| : 25 \\[0.8em] \lambda &= -0{,}3 \end{align*}\]
Parameterwert \(\lambda = -0{,}3\) in \(l\) einsetzen:
\[W \in l\,\colon \enspace \overrightarrow{W} = \begin{pmatrix} 5 \\ 6{,}5 \\ 3 \end{pmatrix} - 0{,}3 \cdot \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix} = \begin{pmatrix} 5 \\ 5{,}6 \\ 1{,}8 \end{pmatrix} \quad \Longrightarrow \quad W\,(5|5{,}6|1{,}8) \]
Radius \(r\) der Kugel
Länge der Strecke \([MW]\) berechnen:
\[M\,(5|6{,}5|3)\, \quad W\,(5|5{,}6|1{,}8)\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}\overline{MW} &= \vert \overrightarrow{MW} \vert \\[0.8em] &= \left| \overrightarrow{W} - \overrightarrow{M} \right| \\[0.8em] &= \left| \begin{pmatrix} 5 \\ 5{,}6 \\ 1{,}8 \end{pmatrix} - \begin{pmatrix} 5 \\ 6{,}5 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ -0{,}9 \\ -1{,}2 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + (-0{,}9)^2 + (-1{,}2)^2} \\[0.8em] &= \sqrt{2{,}25} \\[0.8em] &= 1{,}5 \end{align*}\]
\[\Longrightarrow \quad r = 1{,}5\]
2. Lösungsansatz: Abstand Punkt - Ebene, Schnittpunkt Lotgerade/Kugel
Radius \(r\) der Kugel

Der Radius \(\,r\,\) der Kugel ist gleich dem Abstand \(\,d\,(M;E)\,\) des Mittelpunktes von der Ebene \(\,E\,\).
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
Aus Teilaufgabe b ist bekannt:
\[E\,\colon \enspace 3x_2 + 4x_3 - 24 = 0\,; \quad \overrightarrow{n}_E = \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\]
Betrag des Normalenvektors der Ebene \(E\,\):
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\vert \overrightarrow{n}_E \vert = \left| \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix} \right| = \sqrt{0^2 + 3^2 + 4^2} = \sqrt{25} = 5 \]
\[E^{HNF}\colon \enspace \frac{3x_2 + 4x_3 - 24}{5} = 0\]
Abstand \(d\,(M; E)\) berechnen:
\[M\,(5|6{,}5|3)\]
\[\begin{align*}d\,(M, E) &= \left| \frac{3m_2 + 4m_3 - 24}{5} \right| \\[0.8em] &= \left| \frac{3 \cdot 6{,}5 + 4 \cdot 3 - 24}{5} \right| \\[0.8em] &= \left| \frac{7{,}5}{5} \right| = 1{,}5 \end{align*}\]
\[\Longrightarrow \quad r = 1{,}5\]
Koordinaten des Punktes \(W\)
Lotgerade \(l\) mit \(M \in l\) auf die Ebene \(E\) bestimmen:
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\[M\,(5|6{,}5|3)\,, \quad \overrightarrow{n}_E = \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\]
\[\begin{align*} l\,\colon \enspace \overrightarrow{X} &= \overrightarrow{M} + \lambda \cdot \overrightarrow{n}_E \\[0.8em] \overrightarrow{X} &= \begin{pmatrix} 5 \\ 6{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\,, \quad \lambda \in \mathbb R \end{align*}\]
Kugelgleichung aufstellen:
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
Es sei \(K\) die Kugel mit dem Mittelpunkt \(M\,(5|6{,}5|3)\) und dem radius \(r = 1{,}5\,\).
\[K\,\colon \enspace (x_1 - 5)^2 + (x_2 - 6{,}5)^2 + (x_3 - 3)^2 = 2{,}25\]
Schnittpunkte der Lotgeraden \(l\) mit der Kugel \(K\) bestimmen:
Zur Berechnung der Schnittpunkte setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) aus der Geradengleichung von \(l\) in die Kugelgleichung der Kugel \(K\) ein und löst die Gleichung nach dem Parameter \(\lambda\) auf.
\[l\,\colon \enspace \overrightarrow{X} = \begin{pmatrix} 5 \\ 6{,}5 \\ 3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix}\]
\[K\,\colon \enspace (x_1 - 5)^2 + (x_2 - 6{,}5)^2 + (x_3 - 3)^2 = 2{,}25\]
\[\begin{align*} l \cap K\,\colon \enspace (5 - 5)^2 + (6{,}5 + 3\lambda - 6{,}5)^2 + (3 + 4\lambda - 3)^2 &= 2{,}25 \\[0.8em] 9\lambda^2 + 16\lambda^2 &= 2{,}25 \\[0.8em] 25\lambda^2 &= 2{,}25 & &| : 25 \\[0.8em] \lambda^2 &= 0{,}09 & &| \; \sqrt{\quad} \\[0.8em] \lambda_{1,2} &= \pm \, 0{,}3\end{align*}\]
Parameterwerte \(\lambda_1 = -0{,}3\) und \(\lambda_2 = 0{,}3\) in \(l\) einsetzen:
\[\overrightarrow{X}_1 = \begin{pmatrix} 5 \\ 6{,}5 \\ 3 \end{pmatrix} - 0{,}3 \cdot \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix} = \begin{pmatrix} 5 \\ 5{,}6 \\ 1{,}8 \end{pmatrix} \quad \Longrightarrow \quad X_1\,(5|5{,}6|1{,}8)\]
\[\overrightarrow{X}_2 = \begin{pmatrix} 5 \\ 6{,}5 \\ 3 \end{pmatrix} + 0{,}3 \cdot \begin{pmatrix} 0 \\ 3 \\ 4 \end{pmatrix} = \begin{pmatrix} 5 \\ 7{,}4 \\ 4{,}2 \end{pmatrix} \quad \Longrightarrow \quad X_2\,(5|7{,}4|4{,}2)\]
Die Lotgerade \(l\) schneidet die Kugel \(K\) in den Punkten \(X_1\) und \(X_2\). Der Schnittpunkt, der zugleich die Ebenengleichung der Ebene \(E\) erfüllt, ist der gesuchte Punkt \(W\,\).
\[E\,\colon \enspace 3x_2 + 4x_3 - 24 = 0\]
\[X_1 \; \text{in} \; E\,\colon \enspace 3 \cdot 5{,}6 + 4 \cdot 1{,}8 - 24 = 0 \quad \Longrightarrow \quad X_1 \in E \quad \Longrightarrow \quad X_1 = W\]
\[X_2 \; \text{in} \; E\,\colon \enspace 3 \cdot 7{,}4 + 4 \cdot 4{,}2 - 24 = 15 \quad \Longrightarrow \quad X_2 \notin E\]
\[\Longrightarrow \quad W\,(5|5{,}6|1{,}8)\]

Schnittpunkte der Lotgeraden \(l\) mit \(M \in l\) und der Kugel.