Gegeben ist die Ebene E:2x1+x2−2x3=−18.

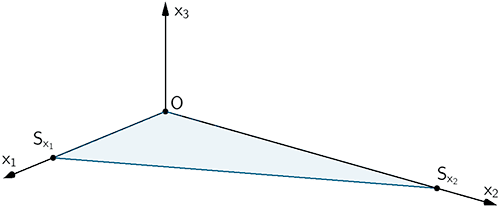
Der Schnittpunkt von E mit der x1-Achse, der Schnittpunkt von E mit der x2-Achse und der Koordinatenursprung sind die Eckpunkte eines Dreiecks. Bestimmen Sie den Flächeninhalt dieses Dreiecks.

(2 BE)

Lösung zu Teilaufgabe 2a

 

Spurpunkte einer Ebene, Flächeninhalt eines rechtwinkligen Dreiecks

 

Dreieck, das die Schnittpunkte der Ebene E mit den Koordinatenachsen sowie der Koordinatenursprung festlegen 

Planskizze: Die Schnittpunkte Sx1 und Sx2 der Ebene E mit der x1-Achse bzw. mit der x2-Achse (Spurpunkte der Ebene E) bilden zusammen mit dem Koordinatenursprung das rechtwinklige Dreieck OSx1Sx2 mit den Katheten [OSx1] und [OSx2].

 

Koordinaten der Spurpunkte Sx1 und Sx2 berechnen:

 

E:2x1+x2−2x3=−18

 

Der Spurpunkt Sx1 der Ebene E mit der x1-Achse hat die Koordinaten Sx1(x1|0|0).

 

Sx1∈E:2x1+0−2⋅0=−182x1=−18|:2x1=−9

 

⟹Sx1(−9|0|0)

 

Der Spurpunkt Sx2 der Ebene E mit der x2-Achse hat die Koordinaten Sx2(0|x2|0).

 

Sx2∈E:2⋅0+x2−2⋅0=−18x2=−18

 

⟹Sx2(0|−18|0)

 

Flächeninhalt A des Dreiecks OSx1Sx2 berechnen:

 

A=12⋅OSx1―⋅OSx2―=12⋅|Sx1→|⋅|Sx2→|=12⋅|(−900)|⋅|(0−180)|=12⋅(−9)2+02+02⋅02+(−18)2+02=12⋅9⋅18=81

 

Alternative: Flächeninhalt A mithilfe des Vektorprodukts berechnen:

Der Vollständigkeit halber sei diese hier eher umständliche Alternative erwähnt.

Vektorprodukt - Flächeninhalt eines Parallelogramms/Dreiecks

Anwendung des Vekorprodukts

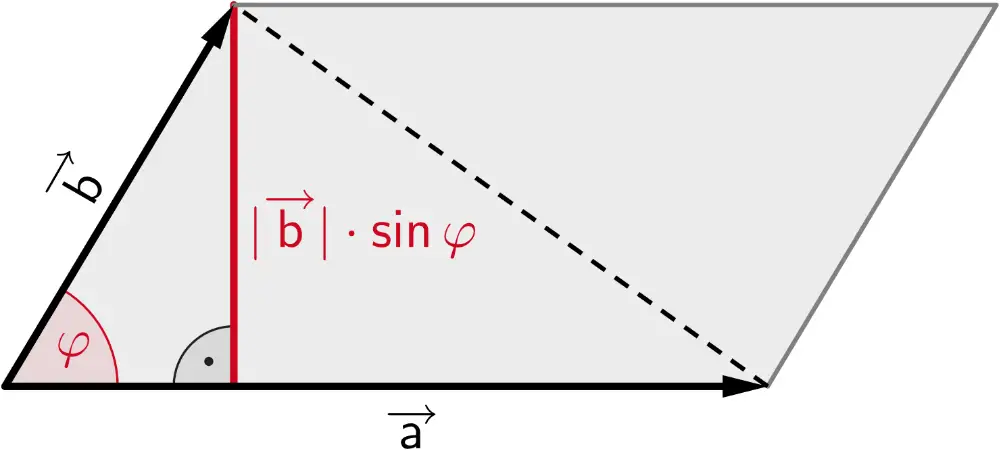
Der Betrag des Vektorprodukts a→×b→ entspricht der Maßzahl des Flächeninhalts eines von zwei Vektoren a→≠0→ und b→≠0→ aufgespannten Parallelogramms.

|a→×b→|=|a→|⋅|b→|⋅sin⁡φ

Anwendung des Vektorprodukts: Berechnung des Flächeninhalts eines Parallelogramms bzw. eines Dreiecks

Flächeninhalt eines Parallelogramms

A=|a→×b→|

Flächeninhalt eines Dreiecks

A=12⋅|a→×b→|

Vektorprodukt

Vektorprodukt (Kreuzprodukt)

Das Vektorprodukt a→×b→ zweier Vektoren a→ und b→ erzeugt einen neuen Vektor c→=a→×b→ mit den Eigenschaften:

c→ ist sowohl zu a→ als auch zu b→ senkrecht.

c→=a→×b→⟹c→⊥a→,c→⊥b→

Der Betrag des Vektorprodukts zweier Vektoren a→ und b→ ist gleich dem Produkt aus den Beträgen der Vektoren a→ und b→ und dem Sinus des von ihnen eingeschlossenen Winkels φ.

|a→×b→|=|a→|⋅|b→|⋅sin⁡φ(0∘≤φ≤180∘)

Die Vektoren a→, b→ und c→ bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist a→ in Richtung des Daumens und b→ in Richtung des Zeigefingers, dann weist c→=a→×b→ in Richtung des Mittelfingers.

Berechnung eines Vektorprodukts im R3 (vgl. Merkhilfe)

a→×b→=(a1a2a3)×(b1b2b3)=(a2⋅b3−a3⋅b2a3⋅b1−a1⋅b3a1⋅b2−a2⋅b1)

A=12⋅|Sx1→×Sx2→|=12⋅|(−900)×(0−180)|=12⋅|(0⋅0−0⋅(−18)0⋅0−(−9)⋅0(−9)⋅(−18)−0⋅0)|=12⋅|(00162)|=12⋅02+02+1622=12⋅162=81

 

Der Flächeninhalt des Dreiecks, das der Schnittpunkt der Ebene E mit der x1-Achse, der Schnittpunkt der Ebene E mit der x2-Achse und der Koordinatenursprung festlegen, beträgt 81 FE (Flächeneinheiten).