Der Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto \frac{1}{4}x^2\) und die Gerade mit der Gleichung \(y = 1\) schließen ein Flächenstück ein (vgl. Abbildung). Durch Rotation diese Flächenstücks um die \(y\)-Achse wird ein Körper erzeugt. Bestimmen Sie das Volumen dieses Körpers.
(5 BE)
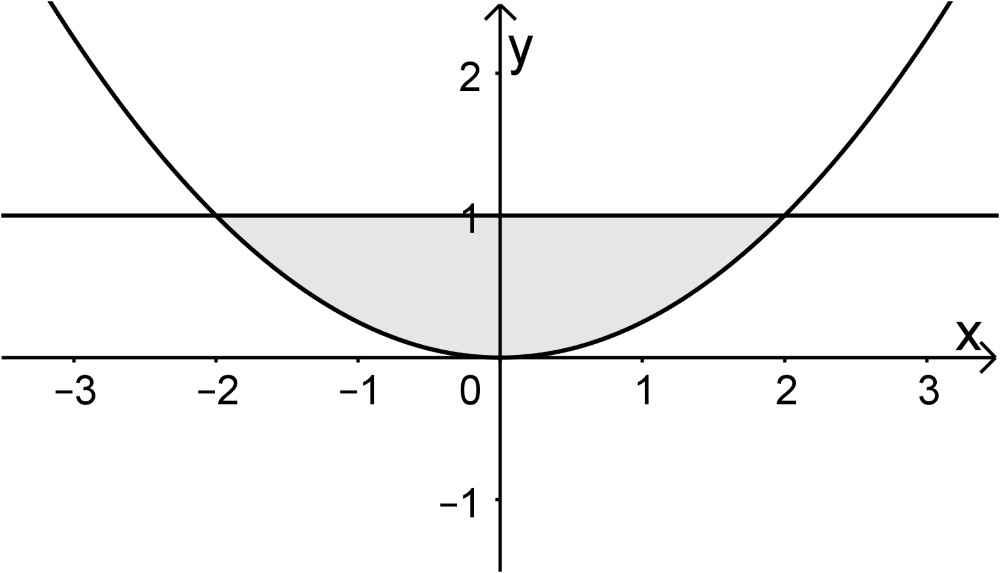
Lösung zu Aufgabe A6
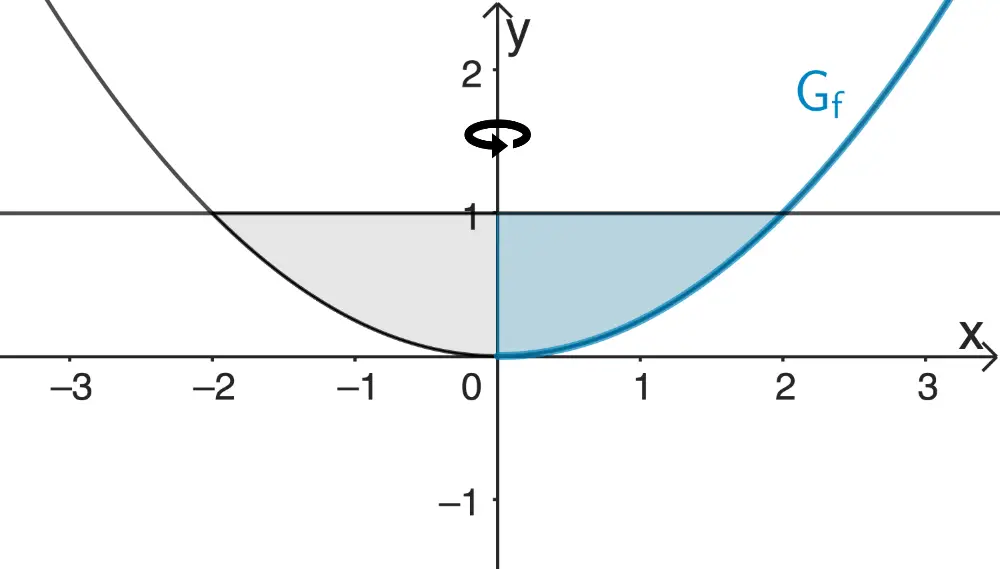
Rotation des Graphen der Funktion \(f\) um die \(y\)-Achse
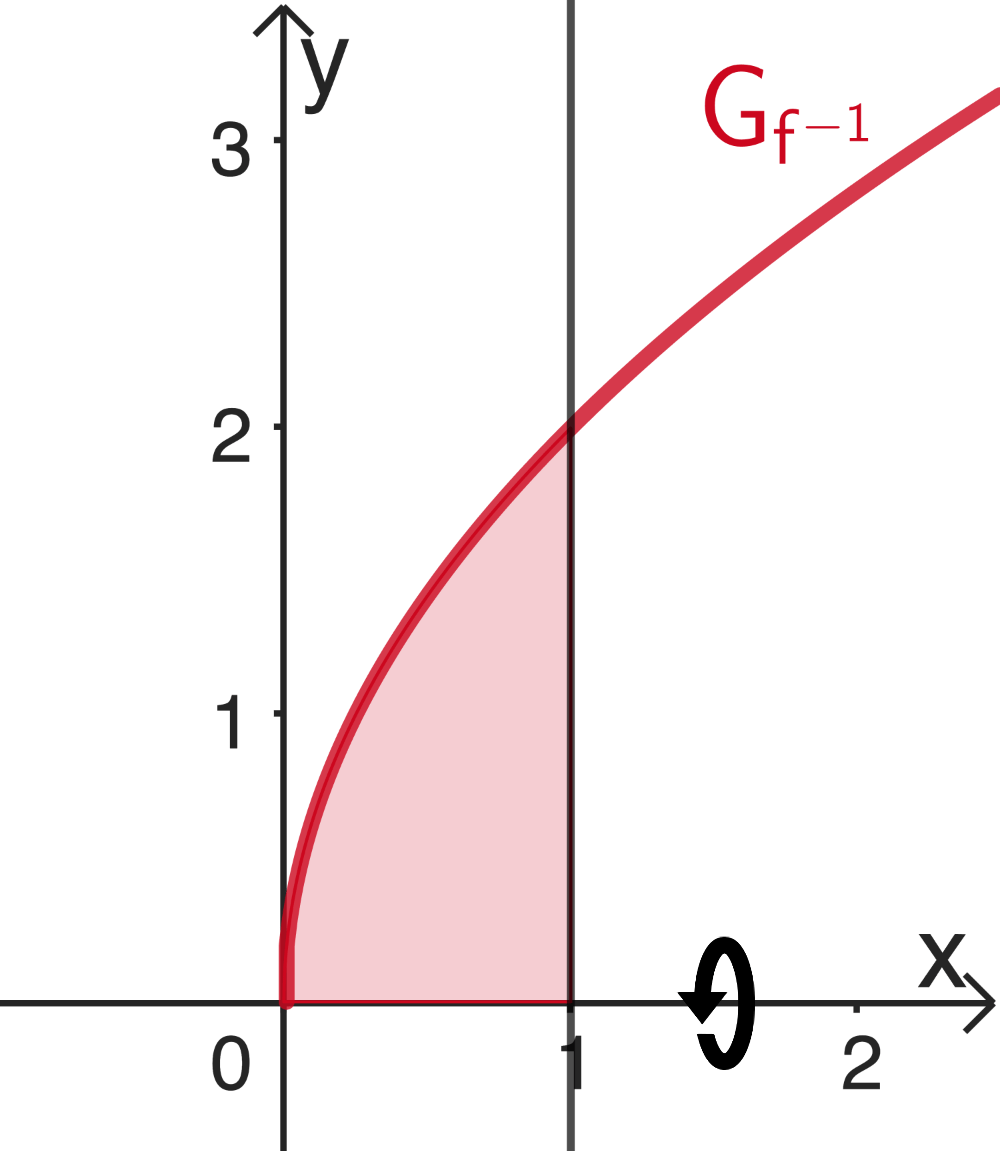
Rotation des Graphen der Umkehrfunktion von \(f\) um die
\(x\)-Achse
Der Graph der Funktion \(f\) ist für \(x \geq 0\) streng monoton steigend. Somit ist die Funktion \(f\) für \(x \geq 0\) umkehrbar.
Kriterium für die Umkehrbarkeit einer Funktion
Ist eine Funktion \(f\) auf ihrem Definitionsbereich bzw. einem Teilbereich des Definitionsbereichs entweder nur streng monoton zunehmend oder nur streng monoton abnehmend, ist sie dort umkehrbar.
Graphische Untersuchung der Umkehrbarkeit: Wenn jede Parallele zur \(x\)-Achse den Funktionsgraphen höchstens einmal schneidet, ist die Funktion im dargestellten Bereich umkehrbar.

Graph einer im dargestellten Bereich umkehrbaren Funktion

Graph einer im dargestellten Bereich nicht umkehrbaren Funktion
Die Aufgabenstellung wird mithilfe der Umkehrfunktion von \(f\) auf eine Rotation um die \(x\)-Achse zurückgeführt. Hierfür wird die Fläche unter dem Graphen der Umkehrfunktion \(\textcolor{#cc071e}{f^{-1}}\) über dem Intervall \([0;1]\) betrachtet.
Umkehrfunktion \(\boldsymbol{f^{-1}}\) bestimmen
Funktionsterm einer Umkehrfunktion bestimmen
1. Funktionsgleichung \(y = f(x)\) nach \(x\) auflösen.
2. Variablen \(x\) und \(y\) tauschen.
3. Funktionsterm \(y = f^{-1}(x)\) mit Definitions- und Wertemenge angeben. Es gilt: \(D_{f^{-1}} = W_f\) und \(W_{f^{-1}} = D_f\).
Es ist ebenso möglich, zuerst die Variablen zu tauschen, und anschließend die Gleichung \(x = f(y)\) nach \(y\) aufzulösen.
Funktionsgraph einer Umkehrfunktion skizzieren
Der Graph \(\textcolor{#cc071e}{G_{f^{-1}}}\) der Umkehrfunktion entsteht durch Spiegelung des Graphen \(G_f\) an der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(\textcolor{#e9b509}{y = x}\). Existieren Schnittpunkte von \(G_f\) mit der Winkelhalbierenden, sind diese Fixpunkte der Spiegelung und somit Schnittpunkte von \(G_f\) und \(\textcolor{#cc071e}{G_{f^{-1}}}\).

Für \(x \geq 0\) gilt:
\[\begin{align*}\textcolor{#0087c1}{f(x)}\; &\textcolor{#0087c1}{= \frac{1}{4}x^2} \\[0.8em] y &= \frac{1}{4}x^2 &&| \cdot 4 \\[0.8em] 4y &= x^2 &&| \; \sqrt{\quad}\; (x \geq 0) \\[0.8em] \sqrt{4y} &= x &&|\; x \leftrightarrow y \; \text{(Variablentausch)} \\[0.8em] y &= \sqrt{4x} \\[0.8em] \textcolor{#cc071e}{f^{-1}(x)}\; &\textcolor{#cc071e}{= \sqrt{4x}} \end{align*}\]
Volumen des Rotationskörpers bestimmen
Volumenberechnung durch Integration

Rotiert die Fläche unter dem Graphen einer Funktion \(f\) über dem Intervall \([a;b]\) um die \(x\)-Achse, entsteht ein Rotationskörper mit dem Volumen \(V\).
\[V = \pi \cdot \int_a^b \left( f(x) \right)^2 dx\]
![Volumenberechnung durch Integration: Rotation des Graphen einer Funktion f über dem Intervall [a;b] um die x-Achse](/images/stories/Merkhilfen_G9/Volumenberechnung_Integration_1_web.png)
Rotiert die Fläche zwischen den Graphen zweier Funktionen \(\textcolor{#cc071e}{f}\) und \(\textcolor{#0087c1}{g}\) über dem Intervall \([a;b]\) um die \(x\)-Achse, entsteht ein „hohler" Rotationskörper mit dem Volumen \(V\).
\[V = \pi \cdot \int_a^b \left(\left( \textcolor{#cc071e}{f(x)} \right)^2 - \left( \textcolor{#0087c1}{g(x)} \right)^2\right) dx\]
![Volumenberechnung durch Integration: Rotation der Fläche zwischen den Graphen zweier Funktionen f und g über dem Intervall [a;b] um die x-Achse](/images/stories/Merkhilfen_G9/Volumenberechnung_Integration_2_web.png)
Mit \(\displaystyle V = \pi \cdot \int_a^b \left(\left( \textcolor{#cc071e}{f(x)} \right)^2 - \left( \textcolor{#0087c1}{g(x)} \right)^2\right) dx = \pi \cdot \int_a^b \left( \textcolor{#cc071e}{f(x)} \right)^2 dx - \pi \cdot \int_a^b \left( \textcolor{#0087c1}{g(x)} \right)^2 dx\) ist es ebenso möglich, die Volumen der beiden Rotationskörper, die durch Rotation der Flächen unter den Graphen von \(f\) bzw. \(g\) um die \(x\)-Achse hervorgehen, getrennt zu berechnen, und diese voneinander zu subtrahieren.
Rotiert eine Fläche um die \(y\)-Achse, die von dem Graphen einer Funktion \(f\) und den Geraden mit den Gleichungen \(y = a\) und \(y = b\) sowie der \(y\)-Achse begrenzt wird, entsteht ein Rotationskörper mit dem Volumen \(V\)
\[V = \pi \cdot \int_a^b \left( f^{-1}(x)\right)^2 dx\]
Dabei ist \(f^{-1}\) die Umkehrfunktion von \(f\). Voraussetzung ist, dass diese auf dem Intervall \([a;b]\) existiert.

\[\begin{align*} V &= \pi \cdot \int_0^1 \left( \textcolor{#cc071e}{f^{-1}(x)} \right)^2 dx \\[0.8em] &= \pi \cdot \int_0^1 \left( \textcolor{#cc071e}{\sqrt{4x}} \right)^2 dx \\[0.8em] &= \pi \cdot \int_0^1 4x dx \\[0.8em] &= \pi \cdot \left[ 2x^2 \right]_0^1 \\[0.8em] &= \pi \cdot \left( 2 \cdot 1^2 - 2 \cdot 0^2 \right) \\[0.8em] &= 2\pi \end{align*}\]
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.3.6 Anwendungen der Integralrechnung - Volumenberechnungen)


