Für \(0 \leq x \leq 5\) gilt, dass der Graph von \(f\) und der Graph einer trigonometrischen Funktion \(h\)
● die gleichen Schnittpunkte mit der \(x\)-Achse besitzen,
● beide nicht unterhalb der \(x\)-Achse verlaufen,
● jeweils mit der \(x\)-Achse eine Fläche des Inhalts \(\frac{625}{72}\) einschließen.
Bestimmen Sie einen Term einer solchen Funktion \(h\).
(6 BE)
Lösung zu Teilaufgabe 1g
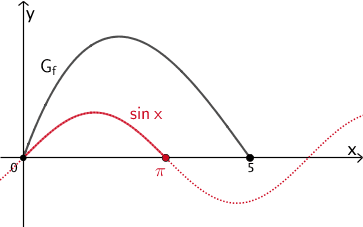
Der Graph der Sinusfunktion \(x \mapsto \sin{x}\) verläuft zwischen den Nullstellen \(x = 0\) und \(x = \pi\) oberhalb der \(x\)-Achse.
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
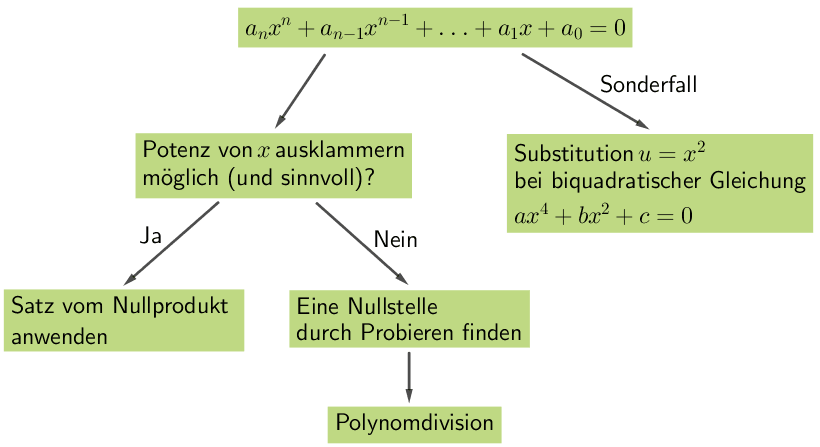
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
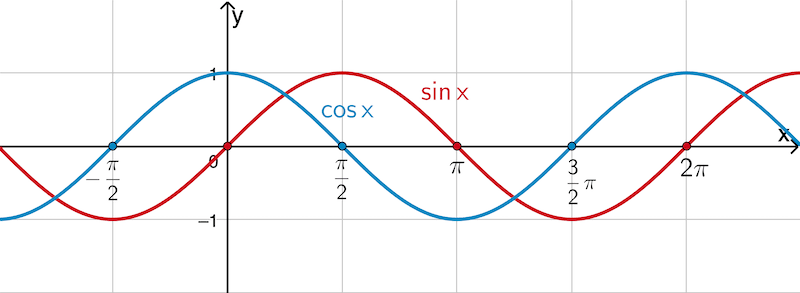
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
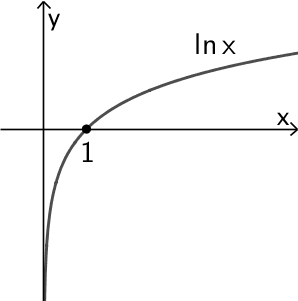
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
Deshalb ist es zweckmäßig, als Ansatz für die Funktion \(h\) ebenfalls eine Sinusfunktion zu wählen.
Allgemeine Sinusfunktion
\[f(x) = a \cdot \sin(bx + c) + d = a \cdot \sin \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
\(h(x) = a \cdot \sin{(bx)}\) mit \(a, b > 0\)
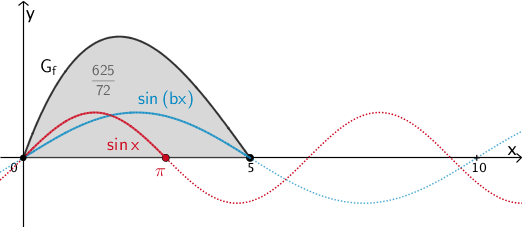
Der Parameter \(b > 0\) bewirkt eine Streckung mit dem Streckungsfaktor \(\dfrac{1}{b}\) des Graphen der Sinusfunktion \(x \mapsto \sin{x}\) in positive \(x\)-Richtung und beeinflusst so die Lage der Nullstelle \(x = \pi\), ohne die Lage der Nullstelle \(x = 0\) zu verändern.
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
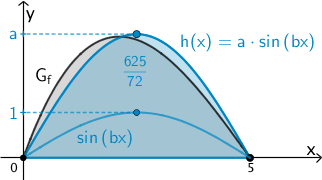
Der Parameter \(a > 0\) bewirkt eine Streckung des Graphen der Sinusfunktion \(x \mapsto \sin{(bx)}\) in \(y\)-Richtung. Die Streckung beeinflusst den Inhalt des Flächenstücks, welches der entstehende Graph \(G_{h}\) für \(0 \leq x \leq 5\) mit der \(x\)-Achse einschließt. Die durch den Parameter \(b\) festgelegten Nullstellen \(x = 0\) und \(x = 5\) bleiben erhalten.
Anmerkung:
Eine Verschiebung in x- bzw. y-Richtung kommt nicht in Frage, da diese jeweils die Lage der Nullstelle \(x = 0\) der Sinusfunktion \(x \mapsto \sin{x}\) unerwünscht verändern würde.
Wert des Parameters \(b\) ermitteln:
\(x = 5\) soll die erste positive Nullstelle von \(h\) sein. Die erste positive Nullstelle der Sinusfunktion ist \(\pi\). Dann muss mit \(h(5) = 0\) gelten:
\[\begin{align*}h(5) &= 0 \\[0.8em] a \cdot \sin{(b \cdot 5)} &= 0 &&| \; \sin{\pi} = 0; \enspace (a \neq 0) \end{align*}\]
\[\Longrightarrow \quad b \cdot 5 = \pi \quad \Longleftrightarrow \quad b = \frac{\pi}{5}\]
Alternative Berechnung von \(b\) mithilfe der Periode \(p\) von \(h\):
Wenn \(x = 5\) die erste positive Nullstelle von \(h\) sein soll, muss die Sinusfunktion \(h\) die Periode \(p = 10\) haben.
Allgemeine Sinusfunktion
\[f(x) = a \cdot \sin(bx + c) + d = a \cdot \sin \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
\[\begin{align*} p = \frac{2\pi}{b} \quad \Longleftrightarrow \quad b &= \frac{2\pi}{p} \\[0.8em] &= \frac{2\pi}{10} \\[0.8em] &= \frac{\pi}{5} \end{align*}\]
\[\Longrightarrow \quad h(x) = a \cdot \sin{\left( \frac{\pi}{5}x \right)}\]
\(b = \dfrac{\pi}{5}\) bedeutet eine Streckung des Graphen der Sinusfunktion \(x \mapsto \sin{x}\) mit dem Streckungsfaktor \(\dfrac{1}{b} = \dfrac{5}{\pi}\).
Wert des Parameters \(a\) ermitteln:
\(G_{h}\) soll für \(0 \leq x \leq 5\) mit der \(x\)-Achse eine Fläche des Inhalts \(\frac{625}{72}\) einschließen. Der Wert des bestimmten Integrals \(\displaystyle \int_{0}^{5}h(x)dx\) kann als Maßzahl dieses Flächeninhalts interpretiert werden.
\[\begin{align*}\Longrightarrow \quad \int_{0}^{5}h(x)dx &= \frac{625}{72} \\[0.8em] \int_{0}^{5} a \cdot \sin\left( \frac{\pi}{5}x \right) dx &= \frac{625}{72} \end{align*}\]
Durch Auflösen des Integrals \(\displaystyle \int_{0}^{5} a \cdot \sin\left( \frac{\pi}{5}x \right) dx\) ergibt sich eine Gleichung zur Bestimmung des Parameters \(a\).
Für die Berechnung des bestimmten Integrals \(\displaystyle \int_{0}^{5}h(x)dx\) wird eine Stammfunktion der Integrandenfunktion \(h(x) = a \cdot \sin{\left( \dfrac{\pi}{5}x \right)}\) benötigt. Die Menge aller Stammfunktionen von \(h\) ist gegeben durch das unbestimmte Integral \(\displaystyle \int h(x)dx\)
Wichtige unbestimmte Integrale (\(C \in \mathbb R\), vgl. Merkhilfe)
\[\int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq - 1)\]
\[\int \frac{1}{x}\,dx = \ln{\vert x \vert} + C\]
\[\int \sin{x} \, dx = -\cos{x} + C\]
\[\int \cos{x} \, dx = \sin{x} + C\]
\[\int e^{x} dx = e^{x} + C\]
\[\int \ln{x}\, dx = -x + x \cdot \ln{x} + C\]
\[\int \frac{f'(x)}{f(x)} dx = \ln{\vert f(x) \vert} + C\]
\[\int f'(x) \cdot e^{f(x)} dx = e^{f(x)} + C\]
\(\displaystyle \int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C\), wobei \(F\) eine Stammfunktion von \(f\) ist.
Es gilt die Faktorregel und die Summenregel:
\(\displaystyle \int c \cdot f(x)\,dx = c \cdot \int f(x)\,dx\) mit \(c \in \mathbb R\)
\( \displaystyle \int \left[f(x) \pm g(x) \right] dx = \int f(x)\,dx \pm \int g(x)\,dx\)
\[\begin{align*}\int h(x)dx &= \int a \cdot \sin{\left( \frac{\pi}{5}x \right)} \\[0.8em] &= a \cdot \frac{1}{\frac{\pi}{5}} \cdot \left( -\cos{\left( \frac{\pi}{5}x \right)} \right) + C \\[0.8em] &= a \cdot \frac{5}{\pi} \cdot \left(-\cos\left( \frac{\pi}{5}x \right) \right) + C\end{align*}\]
Für \(C = 0\) ist \(H \colon x \mapsto a \cdot \dfrac{5}{\pi} \cdot \left(-\cos\left( \dfrac{\pi}{5}x \right) \right)\) eine Stammfunktion von \(h\)
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} \int_{0}^{5}h(x)dx &= \frac{625}{72} \\[0.8em] \int_{0}^{5} a \cdot \sin{\left( \frac{\pi}{5}x \right)}dx &= \frac{625}{72} \\[0.8em] \left[ a \cdot \dfrac{5}{\pi} \cdot \left(-\cos\left( \dfrac{\pi}{5}x \right) \right) \right]_{0}^{5} &= \frac{625}{72} \\[0.8em] a \cdot \left[ -\frac{5}{\pi} \cos{\left( \frac{\pi}{5}x \right)} \right]_{0}^{5} &= \frac{625}{72} \\[0.8em] a \cdot \left[ -\frac{5}{\pi} \cos{\left( \frac{\pi}{5} \cdot 5 \right)} - \left( -\frac{5}{\pi} \cos{\left( \frac{\pi}{5} \cdot 0 \right)} \right) \right] &=\frac{625}{72} \\[0.8em] a \cdot \left[-\frac{5}{\pi} \cdot (-1) - \left( -\frac{5}{\pi} \cdot 1 \right) \right] &= \frac{625}{72} \\[0.8em] a \cdot \left( \frac{5}{\pi} + \frac{5}{\pi} \right) &= \frac{625}{72} \\[0.8em] a \cdot \frac{10}{\pi} &= \frac{625}{72} &&| \cdot \frac{\pi}{10} \\[0.8em] a &= \frac{125}{144}\pi \end{align*}\]
\[\Longrightarrow \quad h(x) = \frac{125}{144}\pi \cdot \sin{\left( \frac{\pi}{5}x \right)}\]

