Ein Biologe nimmt an, dass sich das Wachstum der Blumen vor Beobachtungsbeginn näherungsweise durch die Gleichung der Tangente aus Aufgabe 1d beschreiben lässt. Untersuchen Sie mithilfe einer Rechnung, ob diese Annahme damit in Einklang steht, dass vom Zeitpunkt des Auskeimens bis zum Beobachtungsbeginn etwa zwei Wochen vergehen.
(4 BE)
Lösung zu Teilaufgabe 2d
\(t \colon y = 0{,}18x + 0{.}2\;\)(siehe Teilaufgabe 1d)
1. Lösungsansatz: Zeitspanne Auskeimen - Beobachtungsbeginn überprüfen
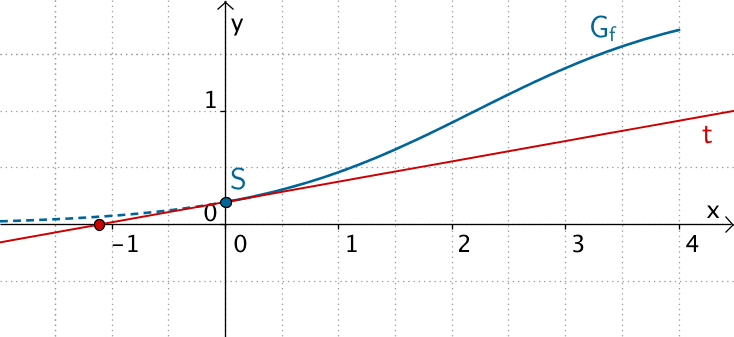
Der Schnittpunkt der Tangente \(t\) mit der \(x\)-Achse (Zeitachse) beschreibt den Zeitpunkt des Auskeimens.
\[\begin{align*} 0{}18x + 0{,}2 &= 0 & &| -0{,}2 \\[0.8em] 0{,}18 &= -0{,}2 & &| : 0{,}18 \\[0.8em] x &= -\frac{0{,}2}{0{,}18} \\[0.8em] x &\approx -1{,}1 \end{align*}\]
\[\Longrightarrow \quad 1{,}1\,\text{Monate} > 2\,\text{Wochen}\]
Die Annahme des Biologen steht nicht im Einklang mit den zwei Wochen, die vom Zeitpunkt des Auskeimens bis zum Beobachtungsbeginn vergehen.
2. Lösungsansatz: Höhe der Sonnenblumen überprüfen
\[t(x) = 0{,}18x + 0{,}2\]
\[2\,\text{Wochen} = 0{,}5\,\text{Monate}\]
\[t(-0{,}5) = 0{,}18 \cdot -0{,}5 + 0{,}2 = 0{,}11\]
Nach der Annahme des Biologen wären die Sonnenblumen zum Zeitpunkt des Auskeimens (2 Wochen vor Beobachtungsbeginn) bereits 11 cm hoch. Folglich widerspricht die Annahme des Biologen dem Zeitpunkt des Auskeimens.


