Ermitteln Sie die Koordinaten des Eckpunkts \(S\) der Raute \(PQRS\). Zeigen Sie, dass \(PQRS\) kein Quadrat ist.
(2 BE)
Lösung zu Teilaufgabe 1b
Koordinaten des Eckpunkts \(S\)
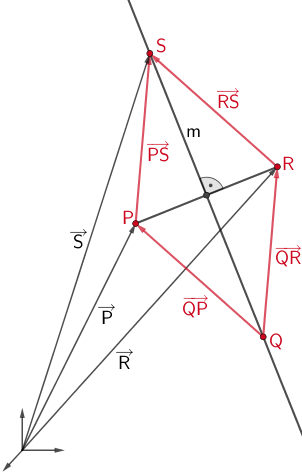
Der Punkt \(S\) liegt ebenfalls auf der Mittelsenkrechten \(m\) der Strecke \([PR]\) (vgl. Teilaufgabe 1a). Er ist beispielsweise der Bildpunkt einer Verschiebung von \(\textcolor{#cc071e}{P}\) um den Verbindungsvektor \(\textcolor{#cc071e}{\overrightarrow{QR}}\) oder einer Verschiebung von \(\textcolor{#cc071e}{R}\) um den Verbindungsvektor \(\textcolor{#cc071e}{\overrightarrow{QP}}\).
Es gilt: \(\textcolor{#cc071e}{\overrightarrow{PS} = \overrightarrow{QR}}\) und \(\textcolor{#cc071e}{\overrightarrow{RS} = \overrightarrow{QP}}\)
Damit lässt sich der Ortsvektor \(\overrightarrow{S}\) des Punktes \(S\) durch Vektoraddition wie folgt berechnen:
\(P(-2|3|0)\), \(R(2|-1|2)\), \(Q(-2|1|5)\) (\(q = -2\), vgl. Teilaufgabe 1a)
\[\begin{align*}\overrightarrow{S} &= \overrightarrow{P} + \textcolor{#cc071e}{\overrightarrow{PS}} &&| \; \textcolor{#cc071e}{\overrightarrow{PS} = \overrightarrow{QR}} \\[0.8em] &= \overrightarrow{P} + \overrightarrow{QR} \\[0.8em] &= \overrightarrow{P} + (\overrightarrow{R} - \overrightarrow{Q}) \\[0.8em] &= \begin{pmatrix} -2 \\ 3 \\ 0 \end{pmatrix} + \left[ \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix} - \begin{pmatrix} -2 \\ 1 \\ 5 \end{pmatrix} \right] \\[0.8em] & = \begin{pmatrix} -2 \\ 3 \\ 0 \end{pmatrix} + \begin{pmatrix} 4 \\ -2 \\ -3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad S(2|1|-3)\]
oder
\[\begin{align*}\overrightarrow{S} &= \overrightarrow{R} + \textcolor{#cc071e}{\overrightarrow{RS}} &&| \; \textcolor{#cc071e}{\overrightarrow{RS} = \overrightarrow{QP}} \\[0.8em] &= \overrightarrow{R} + \overrightarrow{QP} \\[0.8em] &= \overrightarrow{R} + (\overrightarrow{P} - \overrightarrow{Q}) \\[0.8em] &= \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix} + \left[ \begin{pmatrix} -2 \\ 3 \\ 0 \end{pmatrix} - \begin{pmatrix} -2 \\ 1 \\ 5 \end{pmatrix} \right] \\[0.8em] &= \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix} + \begin{pmatrix} 0 \\ 2 \\ -5 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad S(2|1|-3)\]
Nachweis, dass die Raute \(PQRS\) kein Quadrat ist
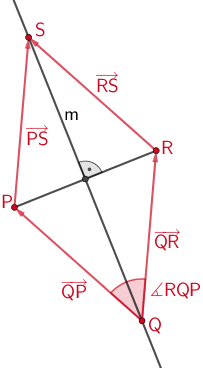
Die Raute \(PQRS\) ist kein Quadrat, wenn einer der Innenwinkel ungleich 90° ist, beispielsweise wenn der Winkel \(\textcolor{#cc071e}{\measuredangle RQP}\) ungleich 90° ist. Dies ist dann der Fall, wenn das Skalarprodukt der Verbindungsvektoren \(\textcolor{#cc071e}{\overrightarrow{QR}}\) und \(\textcolor{#cc071e}{\overrightarrow{QP}}\) ungleich Null ist
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\(\overrightarrow{QP} = \begin{pmatrix} 0 \\ 2 \\ -5 \end{pmatrix}\); \(\overrightarrow{QR} = \begin{pmatrix} 4 \\ -2 \\ -3 \end{pmatrix}\) (vgl. oben)
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \textcolor{#cc071e}{\overrightarrow{QR} \circ \overrightarrow{QP}} &= \begin{pmatrix} 4 \\ -2 \\ -3 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 2 \\ -5 \end{pmatrix} \\[0.8em] &= 4 \cdot 0 + (-2) \cdot 2 + (-3) \cdot (-5) \\[0.8em] &= 11 \textcolor{#cc071e}{\neq 0} \end{align*}\]
\[\Longrightarrow \quad \textcolor{#cc071e}{\measuredangle RQP \neq 90^{\circ}}\]
Also ist die Raute \(PQRS\) kein Quadrat.


