Aus energetischen Gründen soll der Abstand der beiden Stellen, an denen die beiden Bohrkanäle auf die wasserführende Gesteinsschicht treffen, mindestens 1500 m betragen. Entscheiden Sie auf der Grundlage des Modells, ob diese Bedingung für jeden möglichen zweiten Bohrkanal erfüllt wird.
(4 BE)
Lösung zu Teilaufgabe f
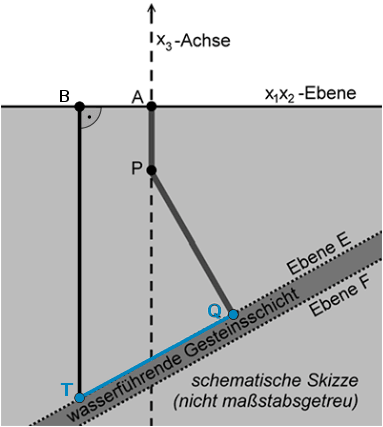
Im Modell sind \(\textcolor{#0087c1}{Q(1|1|-3{,}5)}\) und \(\textcolor{#0087c1}{T(t|-t|-4{,}3)}\) die beiden Stellen, an denen die beiden Bohrkanäle auf die wasserführende Gesteinsschicht treffen.
Es muss \(\textcolor{#0087c1}{d(Q;T) = \overline{QT} \geq 1{,}5}\) gelten.
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \textcolor{#0087c1}{\overline{QT}} &= \vert \overrightarrow{QT} \vert = \vert \overrightarrow{T} - \overrightarrow{Q} \vert \\[0.8em] &= \left| \begin{pmatrix} t \\ -t \\ -4{,}3 \end{pmatrix} - \begin{pmatrix} 1 \\ 1 \\ -3{,}5 \end{pmatrix} \right| = \left| \begin{pmatrix} t - 1 \\ -1 - 1 \\ -0{,}8 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(t - 1)^{2} + (-1 - 1)^{2} + (-0{,}8)^{2}} &&| \; (a - b)^{2} = a^{2} - 2ab + b^{2} \\[0.8em] &= \sqrt{t^{2} - 2t + 1 + t^{2} + 2t + 1 + 0{,}64} \\[0.8em] &= \sqrt{2t^{2} + 2{,}64} &&| t \in \mathbb R \\[0.8em] &\geq \sqrt{2{,}64} &&(\text{für}\; t = 0) \\[0.8em] & \; \textcolor{#0087c1}{> 1{,}5} &&(\sqrt{2{,}64} \approx 1{,}6) \end{align*}\]
Somit beträgt der Abstand der beiden Stellen, an denen die beiden Bohrkanäle auf die wasserführende Gesteinsschicht treffen, für jeden möglichen zweiten Bohrkanal mindestens 1500 Meter.

