Begründen Sie, dass die Ereignisse \(A\) und \(R\) abhängig sind.
(2 BE)
Lösung zu Teilaufgabe c
Stochastische Abhängigkeit/Unabhängigkeit
Stochastische (Un)Abhängigkeit von zwei Ereignissen
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B)\) gilt. (vgl. Merkhilfe) *
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw.
\(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw.
\(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\) gilt.
Aus Teilaufgabe b ist bekannt:
\[P(A \cap R) = 0{,}42\,; \quad P(A) = 0{,}7\,; \quad P(R) = 0{,}54\]
Ereignisse \(A\) und \(R\) auf stochastische Unabhängigkeit prüfen:
Die Ereignisse \(A\) und \(R\) sind stochastisch unabhängig, wenn \(P(A \cap R) = P(A) \cdot P(R)\) gilt.
\[P(A) \cdot P(R) = 0{,}7 \cdot 0{,}54 = 0{,}378\]
\[\Longrightarrow \quad P(A \cap R) = 0{,}42 \neq 0{,}378 = P(A) \cdot P(R)\]
\(\Longrightarrow \quad\) Die Ereignisse \(A\) und \(R\) sind stochastisch abhängig.
Begründung mit Baumdiagramm:
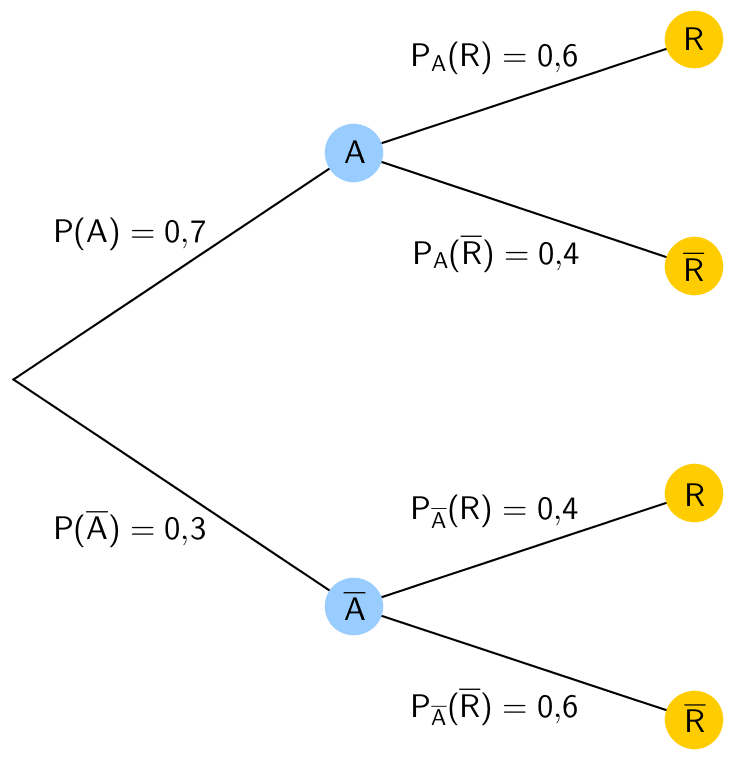
Baumdiagramm aus Teilaufgabe b
Die Ereignisse \(A\) und \(R\) sind stochastisch abhängig, weil an den Ästen der zweiten Stufe des Baumdiagramms aus Teilaufgabe b unterschiedliche Wahrscheinlichkeiten stehen.
Begründung mit Vierfeldertafel:
| \(R\) | \(\overline R\) | ||
| \(A\) | \(P(A \cap R) = 0{,}42\) | \(P(A \cap \overline R) = 0{,}28\) | \(P(A) = 0{,}7\) |
| \(\overline A\) | \(P(\overline A \cap R) = 0{,}12\) | \(P(\overline A \cap \overline R) = 0{,}18\) | \(P(\overline A) = 0{,}3\) |
| \(P(R) = 0{,}54\) | \(P(\overline R) = 0{,}46\) | \(1\) |
Vierfeldertafel aus Teilaufgabe b
\[P(A \cap R) = 0{,}42 \neq 0{,}378 = 0{,}7 \cdot 0{,}54 = P(A) \cdot P(R)\]
\[P(A \cap \overline{R}) = 0{,}28 \neq 0{,}322 = 0{,}7 \cdot 0{,}46 = P(A) \cdot P(\overline{R})\]
\[P(\overline{A} \cap R) = 0{,}12 \neq 0{,}162 = 0{,}3 \cdot 0{,}54 = P(\overline{A}) \cdot P(R)\]
\[P(\overline{A} \cap \overline{R}) = 0{,}18 \neq 0{,}138 = 0{,}3 \cdot 0{,}46 = P(\overline{A}) \cdot P(\overline{R})\]
Die Ereignisse \(A\) und \(R\) sind stochastisch abhängig, weil die Vierfeldertafel keine Multiplikationstafel der Wahrscheinlichkeiten ist. Die Einträge der inneren Felder (Wahrscheinlichkeiten der Schnittmengen) sind nicht das Produkt der Einträge der zugehörigen Randfelder (Wahrscheinlichkeiten der Ereignisse \(A\) und \(R\) bzw. deren Gegenereignisse).


