Zeigen Sie, dass die in \(\mathbb R\) definierte Funktion \(F\) mit \(F(x) = x^2 \cdot e^x\) eine Stammfunktion von \(f\) ist. Geben eine Gleichung einer weiteren Stammfunktion \(G\) von \(f\) an, für die \(G(1) = 2e\) gilt.
(3 BE)
Lösung zu Teilaufgabe 2b
Nachweis der Stammfunktion \(F\)
\[F(x) = x^2 \cdot e^x \,; \quad D = \mathbb R\]
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[F'(x) = f(x)\]
Ableitung einer Potenzfunktion
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
(vgl. Merkhilfe)
\[\begin{align*} F'(x) &= 2x \cdot e^x + x^2 \cdot e^x \\[0.8em] &= e^x \cdot (2x + x^2) \\[0.8em] &= f(x) \end{align*}\]
\(\Longrightarrow \quad\) Die Funktion \(F\) ist eine Stammfunktion von \(f\).
Gleichung einer weiteren Stammfunktion \(G\), für die \(G(1) = 2e\) gilt
Jede Funktion \(G\) mit \(G(x) = F(x) + C \,; \; C \in \mathbb R\) ist wegen \(C' = 0\) eine Stammfunktion von \(f\).
\[\begin{align*}G(x) &= F(x) + C \\[0.8em] &= x^2 \cdot e^x + C \end{align*}\]
\[\begin{align*}G(1) &= 2e \\[0.8em] 1^2 \cdot e^1 & + C = 2e \\[0.8em] e + C &= 2e & &| -e \\[0.8em] C = e \end{align*}\]
\(\Longrightarrow \quad G(x) = x^2 \cdot e^x + e\) ist eine Stammfunktion von \(f\), für die \(G(1) = 2e\) gilt (deren Graph \(G_{G}\) den Punkt \((1|2e)\) enthält).
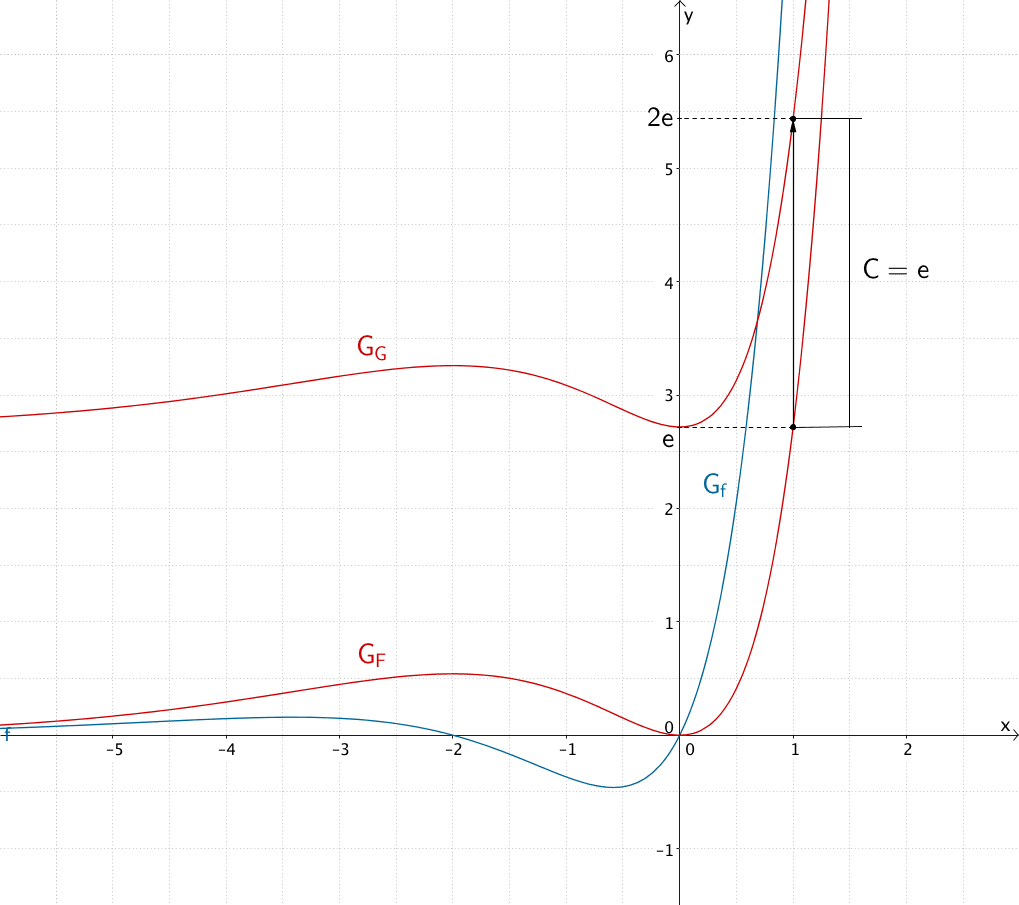
Der Graph der Stammfunktion \(G\) ist gegenüber dem Graphen der Stammfunktion \(F\) um den Wert \(C = e\) in \(y\)-Richtung verschoben.


