Gegeben sind die Punkte \(A(19|0|0)\), \(B(0|19|0)\), \(E(12|0|7)\) und \(F(0|12|7)\) (vgl. Abbildung 1). Das Viereck \(ABFE\) liegt in der Ebene \(L\).
Weisen Sie nach, dass das Viereck \(ABFE\) ein Trapez mit zwei gleich langen Seiten ist.
(3 BE)
Lösung zu Teilaufgabe a
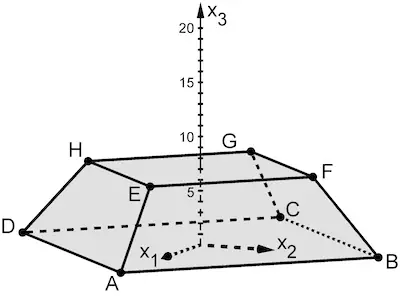
Ein Trapez ist ein Viereck mit zwei zueinander parallelen Seiten. Abbildung 1 lässt vermuten, dass die Seiten \([AB]\) und \([EF]\) zueinander parallel sind.
Nachweis, dass das Viereck \(\boldsymbol{ABFE}\) ein Trapez ist
Die Seiten \([AB]\) und \([EF]\) sind zueinander parallel, wenn die Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{EF}\) ein Vielfaches voneinander sind (linear abhängig sind), d. h. wenn \(\overrightarrow{AB} = k \cdot \overrightarrow{EF}\) mit \(k \in \mathbb R\) gilt.
\(A(19|0|0)\), \(B(0|19|0)\), \(E(12|0|7)\), \(F(0|12|7)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 0\\19\\0 \end{pmatrix} - \begin{pmatrix} 19\\0\\0 \end{pmatrix} = \begin{pmatrix} -19\\19\\0 \end{pmatrix}\]
\[\overrightarrow{EF} = \overrightarrow{F} - \overrightarrow{E} = \begin{pmatrix} 0\\12\\7 \end{pmatrix} - \begin{pmatrix} 12\\0\\7 \end{pmatrix} = \begin{pmatrix} -12\\12\\0 \end{pmatrix}\]
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
\[\overrightarrow{AB} = k \cdot \overrightarrow{EF} \;\Leftrightarrow \; \begin{pmatrix} -19\\19\\0 \end{pmatrix} = k \cdot \begin{pmatrix} -12\\12\\0 \end{pmatrix}; \; k \in \mathbb R\]
\[\Rightarrow \left\{ \begin{align*} -19 &= k \cdot (-12)\; \Rightarrow \; k = \frac{19}{12} \\[0.8em] 19 &= k \cdot 12\; \Rightarrow \; k = \frac{19}{12} \\[0.8em] 0 &= 0 \end{align*} \right\} \Rightarrow \overrightarrow{AB} = \frac{19}{12} \cdot \overrightarrow{EF}\]
\[\Rightarrow \overrightarrow{AB} \parallel \overrightarrow{EF}\]
Also ist das Viereck \(ABFE\) ein Trapez.
Nachweis, dass das Trapez \(\boldsymbol{ABFE}\) zwei gleich lange Seiten hat
Abbildung 1 ist zu entnehmen, dass vermutlich die Seiten \([AE]\) und \([BF]\) gleich lang sind.
\(A(19|0|0)\), \(B(0|19|0)\), \(E(12|0|7)\), \(F(0|12|7)\)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}\overline{AE} &= \vert \overrightarrow{AE} \vert = \vert \overrightarrow{E} - \overrightarrow{A} \vert = \left| \begin{pmatrix} 12\\0\\7 \end{pmatrix} - \begin{pmatrix} 19\\0\\0 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -7\\0\\7 \end{pmatrix} \right| = \sqrt{(-7)^2 + 0^2 + 7^2} = \sqrt{98}\end{align*}\]
\[\begin{align*}\overline{BF} &= \vert \overrightarrow{BF} \vert = \vert \overrightarrow{F} - \overrightarrow{B} \vert = \left| \begin{pmatrix} 0\\12\\7 \end{pmatrix} - \begin{pmatrix} 0\\19\\0 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0\\-7\\7 \end{pmatrix} \right| = \sqrt{0^2 + (-7)^2 + 7^2} = \sqrt{98}\end{align*}\]
\[\Rightarrow\;\overline{AE} = \overline{BF}\]
Somit ist das Viereck \(ABFE\) ein Trapez mit zwei gleich langen Seiten.
