Bestimmen Sie die Wahrscheinlichkeit dafür, dass die fünfte Familie die erste ist, die einen Bollerwagen ausleiht.
(2 BE)
Lösung zu Teilaufgabe 2b
\[P = 0{,}85^{4} \cdot 0{,}15 \approx 0{,}07830 \approx 7{,}8\,\%\]
Ausführliche Erklärung (nicht verlangt)
\(p = \textcolor{#e9b509}{0{,}15}\) (Wahrscheinlichkeit für das Ereignis „Familie entleiht einen Bollerwagen.")
\(1 - p = \textcolor{#0087c1}{0{,}85}\) (Wahrscheinlichkeit für das Ereignis „Familie entleiht keinen Bollerwagen.")
Da die fünfte Familie die erste ist, die einen Bollerwagen ausleiht, leihen die vier Familien davor keinen Bollerwagen aus.
Darüber, ob die nachfolgenden 195 Familien einen Bollerwagen ausleihen oder nicht, liegt keine Aussage vor.
Das heißt, es wird eine Bernoulli-Kette der Länge \(n = 5\) betrachtet und davon ein ganz bestimmter „Pfad", wie nachfolgendes Baumdiagramm veranschaulicht.
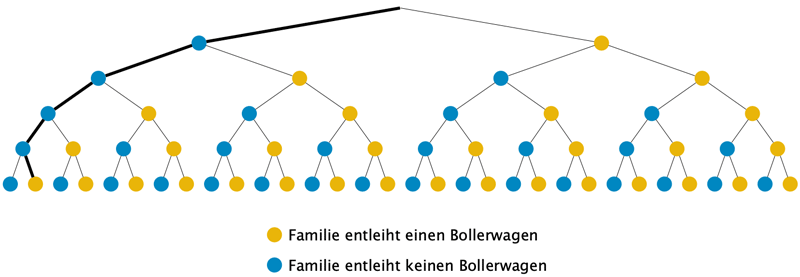
\[\begin{align*}P &= \textcolor{#0087c1}{0{,}85} \cdot \textcolor{#0087c1}{0{,}85} \cdot \textcolor{#0087c1}{0{,}85} \cdot \textcolor{#0087c1}{0{,}85} \cdot \textcolor{#e9b509}{0{,}15} \\[0.8em] &= 0{,}85^{4} \cdot 0{,}15 \\[0.8em] &\approx 0{,}07830 \approx 7{,}8\,\%\end{align*}\]
Anmerkung:
Da die Aufgabenstellung eine Bedingung an die Reihenfolge des Treffers formuliert („... die fünfte Familie die erste ist, die einen Bollerwagen ausleiht."), kann nicht mit der Formel von Bernoulli \(\displaystyle \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k}\) (Binomialverteilung) gerechnet werden. Denn der Binomialkoeffizient \(\displaystyle \binom{n}{k}\) berücksichtigt die Anzahl aller Möglichkeiten wie \(k\) Treffer auf die Länge \(n\) einer Bernoullikette verteilt sein können.


