Um 6 Uhr verläuft der Schatten des Polstabs im Modell durch den Mittelpunkt der Kante \([BC]\), um 12 Uhr durch den Mittelpunkt der Kante \([AB]\) und um 18 Uhr durch den Mittelpunkt der Kante \([AD]\). Begründen Sie, dass der betrachtete Zeitpunkt \(t_{0}\) vor 12 Uhr liegt.
(2 BE)
Lösung zu Teilaufgabe e
Richtungsvektor einer Geraden im Sachzusammenhang beurteilen
\[g\colon \overrightarrow{X} = \begin{pmatrix} 4{,}5 \\ 0 \\ 4{,}5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ 6 \\ -13 \end{pmatrix}\]
\(\overrightarrow{u} = \begin{pmatrix} 6 \\ 6 \\ -13 \end{pmatrix}\) (siehe Teilaufgabe d)
\(A\,(5|-4|0)\,, \enspace B\,(5|4|0)\,, \enspace M\,(2{,}5|0|2)\,, \enspace S\,(4{,}5|0|4{,}5)\) (siehe Teilaufgabe a,c)
Mittelpunkt \(M_{[AB]}\) der Strecke \([AB]\):
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\[\begin{align*}\overrightarrow{M}_{[AB]} &= \frac{1}{2} (\overrightarrow{A} + \overrightarrow{B}) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 5 \\ -4 \\ 0 \end{pmatrix} + \begin{pmatrix} 5 \\ 4 \\ 0 \end{pmatrix} \right] \\[0.8em] &= \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad M_{[AB]} (5|0|0)\]
Parallele Geraden mit dem Richtungsvektor \(\overrightarrow{u}\) repräsentieren im Modell das Sonnenlicht zum Zeitpunkt \(t_{0}\) (siehe Teilaufgabe d). Der Schatten des Polstabs entspricht im Modell der Projektion der Strecke \([MS]\) in die Ebene \(E\) in Richtung des Vektors \(\overrightarrow{u}\).
Die \(x_{2}\)-Koordinate der Punkte \(M\) und \(S\) sowie des Mittelunktes \(M_{[AB]}\) der Strecke \([AB]\) ist jeweils gleich Null. Alle drei Punkte liegen also in der \(x_{1}x_{3}\)-Ebene.
Sonnenlicht, das den Schatten des Polstabs genau auf 12 Uhr projezieren würde (Mittelpunkt \(M_{[AB]}\) der Strecke \([AB]\)), müsste im Modell parallel zur \(x_{1}x_{3}\)-Ebene (\(x_{2} = 0\)) einfallen. Da die \(x_{2}\)-Koordinate des Vektors \(\overrightarrow{u}\) mit \(x_{2} = 6\) jedoch einen positiven Wert hat, muss der betrachtete Zeitpunkt \(t_{0}\) vor 12 Uhr liegen.
![Sonnenlicht durch den Punkt S (Gerade g) und Schatten des Polstabs (Strecke [MS]) zum Zeitpunkt t₀ Sonnenlicht durch den Punkt S (Gerade g) und Schatten des Polstabs (Strecke [MS]) zum Zeitpunkt t₀](/images/stories/B2015_PT_B_G_2/B2015_PT_B_G_2_e_1.png)
Sonnenlicht durch den Punkt \(S\) (Gerade \(g\) mit Richtungsvektor \(\overrightarrow{u}\)) und Schatten des Polstabs (Strecke \([MS]\)) auf der rechteckigen Grundplatte (Rechteck \(ABCD\)) zum Zeitpunkt \(t_{0}\)
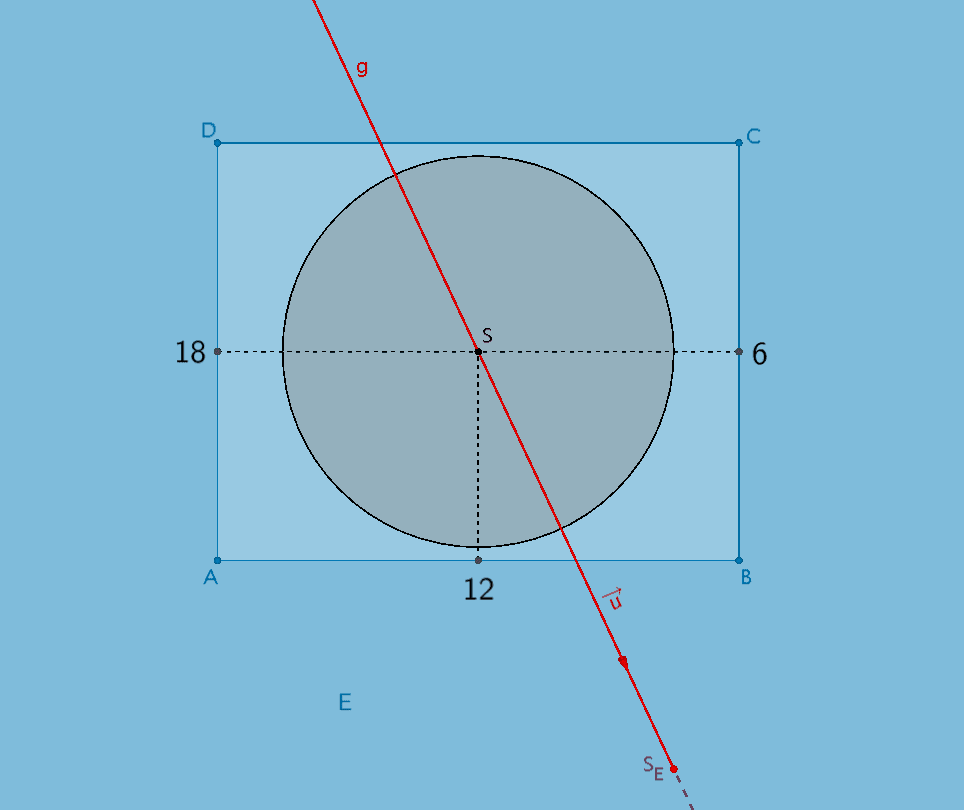
Frontalansicht auf die Ebene \(E\): Sonnenlicht durch den Punkt \(S\) (Gerade \(g\) mit Richtungsvektor \(\overrightarrow{u}\)) zum Zeitpunkt \(t_{0}\)

