Im Raum sind die Eckpunkte eines Dreiecks \(ABC\) gegeben, das weder gleichschenklig noch rechtwinklig ist. Beschreiben Sie in mehreren Teilschritten einen Weg zur Ermittlung der Koordinaten eines Punktes \(D\), durch den sich das Dreieck zum Drachenviereck \(ABCD\) ergänzen lässt.
(4 BE)
Lösung zu Teilaufgabe 2
![Das Drachenviereck ABCD entsteht aus dem Dreieck ABC durch Spiegelung des Punktes B an der Symmetrieachse [AC].](/images/stories/B2014BA_PT_A_G_1/B2014BA_PT_A_G_1_3_01.png "Grafik 1 zur Lösung der Teilaufgabe 3 - Geometrie I - Mathematik Musterabitur Bayern 2011 G8")
Die Diagonalen eines Drachenvierecks stehen senkrecht aufeinander: \(\overline{AC} \perp \overline{BD}\). Die Strecke \([AC]\) des Dreicks \(ABC\) ist Symmetrieachse des Drachenvierecks \(ABCD\). Der Punkt \(D\) ist Spiegelpunkt des Punktes \(B\) an der Symmetrieachse \([AC]\).
1. Lösungsansatz mit Hilfsebene
![Das Drachenviereck ABCD entsteht aus dem Dreieck ABC durch Spiegelung des Punktes B an der Symmetrieachse [AC].](/images/stories/B2014BA_PT_A_G_1/B2014BA_PT_A_G_1_3_02.png "Grafik 2 zur Lösung der Teilaufgabe 3 - Geometrie I - Mathematik Musterabitur Bayern 2011 G8")
1. Hilfsebene \(H\) mit den Eigenschften \(B \in H\) und \(H \perp AC\) bestimmen:
\[\overrightarrow n_H = \overrightarrow{AC}\]
\[H \colon \enspace \overrightarrow{AC} \circ (\overrightarrow B - \overrightarrow X) = 0\]
2. Schnittpunkt \(S\) der Hilfsebene \(H\) mit der Geraden \(AC\) ermitteln:
\[AC \colon \enspace \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow{AC}\]
\[AC \cap H \colon \enspace \overrightarrow{AC} \circ (\overrightarrow B - \overrightarrow A + \lambda \cdot \overrightarrow{AC}) = 0\]
\(\Longrightarrow \quad \lambda_S\;\) (Parameterwert für die Schnittpunktberechnung)
Parameterwert \(\lambda_S\) in \(AC\) einsetzen:
\[S \in AC \colon \enspace \overrightarrow S = \overrightarrow A + \lambda_S \cdot \overrightarrow{AC}\]
3. Koordinaten des Punktes \(D\) berechnen:
\(\overrightarrow D = \overrightarrow B + 2 \cdot \overrightarrow{BS}\enspace\) oder \(\enspace \overrightarrow D = \overrightarrow S + \overrightarrow{BS}\)
2. Lösungsansatz: Anwenden des Skalarproduktes
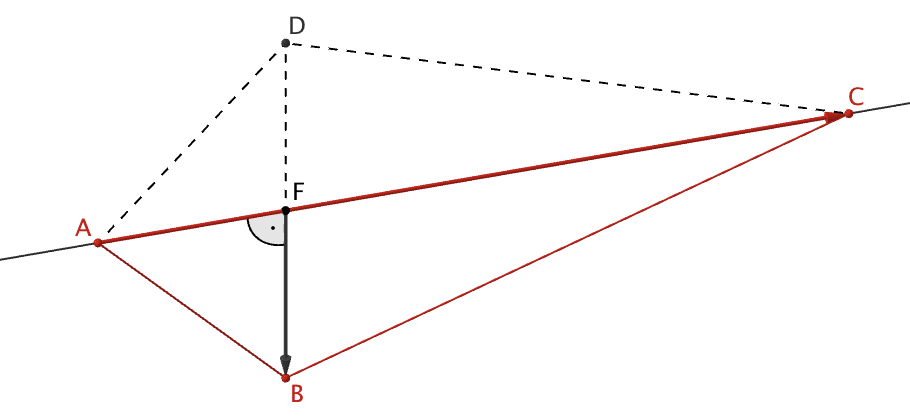
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(B\) auf die Gerade \(AC\).
Somit gilt: \(\enspace \overrightarrow{FB} \perp \overrightarrow{AC} \quad \Longrightarrow \quad \overrightarrow{FB} \circ \overrightarrow{AC} = 0\)
1. Vektor \(\overrightarrow{FB}\) allgemein beschreiben:
\[AC \colon \enspace \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow{AC}\]
\[F \in AC \colon \enspace \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow{AC}\]
\[\begin{align*} \overrightarrow{FB} &= \overrightarrow B - \overrightarrow F \\[0.8em] &= \overrightarrow B - (\overrightarrow A + \lambda \cdot \overrightarrow{AC}) \end{align*}\]
2. Koordinaten des Lotfußpunktes \(F\) bestimmen:
\[\begin{align*} \overrightarrow{FB} \circ \overrightarrow{AC} &= 0 \\[0.8em] \left[ \overrightarrow B - (\overrightarrow A + \lambda \cdot \overrightarrow{AC}) \right] \circ \overrightarrow{AC} &= 0 \end{align*}\]
\(\Longrightarrow \quad \lambda_F\;\) (Parameterwert für die Lotfußpunktberechnung)
Parameterwert \(\lambda_F\) in \(AC\) einsetzen:
\[F \in AC \colon \enspace \overrightarrow F = \overrightarrow A + \lambda_F \cdot \overrightarrow{AC}\]
3. Koordinaten des Punktes \(D\) berechnen:
\(\overrightarrow D = \overrightarrow B + 2 \cdot \overrightarrow{BF}\enspace\) oder \(\enspace \overrightarrow D = \overrightarrow F + \overrightarrow{BF}\)
