Nullstellen einer Funktionenschar
Bewirkt der Parameter \(k\) einer Funktionenschar \(f_{k}\) eine Verschiebung eines Graphen \(G_{g}\) einer Funktion \(g\) im Koordinatensystem oder eine Streckung bzw. Stauchung in \(x\)-Richtung, ändert sich die Lage bzw. Anzahl der Nullstellen der Funktionenschar \(f_{k}\). Eine Streckung in \(y\)-Richtung hat dagegen keinen Einfluss auf die Nullstellen (vgl. Abiturskript - 1.1.7 Entwicklung von Funktionen).
\( f_{k}(x) = g(x) + k\) oder \(f_{k}(x) = g(x + k)\) oder \(f_{k}(x) = g(kx) \quad \Longrightarrow \quad\)Parameter \(k\) beeinflusst Lage bzw. Anzahl und ggf. Art der Nullstellen von \(f_{k}\).
\(f_{k}(x) = k \cdot g(x) \quad \Longrightarrow \quad\) Nullstellen von \(f_{k}\) sind Nullstellen von \(g\).
Beispiel:
Gegeben sei die in \(\mathbb R\) definierte Sinusfunktion \(g \colon x \mapsto \sin{x}\). Betrachtet werden die Nullstellen der folgenden Kurvenscharen:
- a) Die Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto \sin{x} + k\) mit \(k \in \mathbb R \backslash \{0\}\) geht durch Verschiebung des Graphen \(G_{g}\) der Funktion \(g\) um \(k\) in \(y\)-Richtung hervor.
- b) Die Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto \sin{(x + k)}\) mit \(k \in \; ]-2\pi;2\pi[, \; k \neq 0\) geht durch Verschiebung des Graphen \(G_{g}\) der Funktion \(g\) um \(-k\) in \(x\)-Richtung hervor.
- c) Die Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto \sin{(kx)}\) mit \(k \in \mathbb R \backslash \{0\}, \; k > 1\) geht durch Streckung des Graphen \(G_{g}\) der Funktion \(g\) um den Faktor \(\frac{1}{k}\) (Stauchung um Faktor \(k\)) in \(x\)-Richtung hervor.
- d) Die Kurvenschar \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto k \cdot \sin{x}\) mit \(k \in \mathbb R \backslash \{0\}\) geht durch Streckung des Graphen \(G_{g}\) der Funktion \(g\) um den Faktor \(k\) in \(y\)-Richtung hervor.
(vgl. Abiturskript - 1.1.7 Entwicklung von Funktionen)
Der Graph \(G_{g}\) der Sinusfunktion \(g \colon x \mapsto \sin{x}\) besitzt im Intervall \([0;2\pi]\) genau drei Nullstellen: \(x_{1} = 0\), \(x_{2} = \pi\) und \(x_{3} = 2\pi\).
a) \(f_{k}(x) = \sin{x} + k; \; D_{f_{k}} = \mathbb R, \; k \in \mathbb R \backslash \{0\}\)
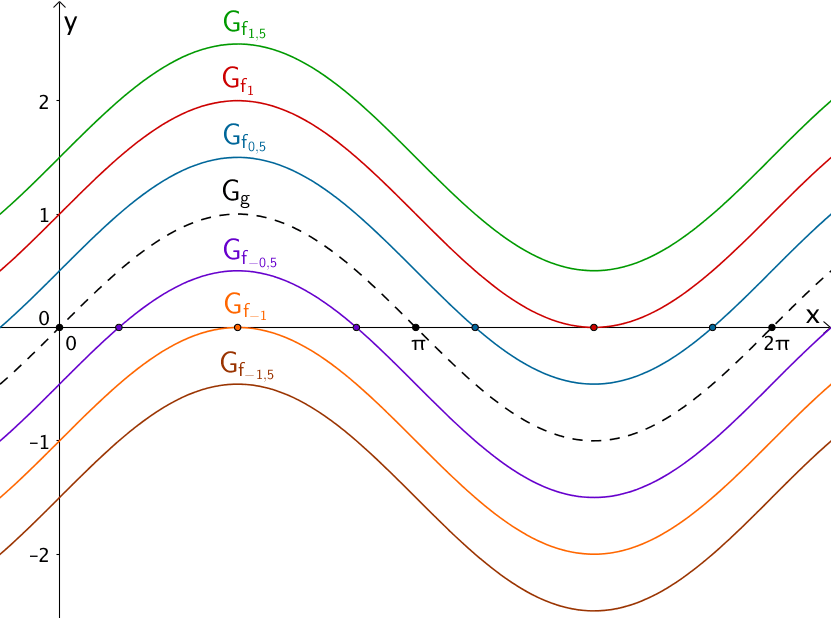
Die Graphen \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto \sin{x} + k\) besitzen abhängig vom Wert des Parameters \(k\) im Intervall \([0;2\pi]\) zwei Nullstellen \((k \in ]-1;1[)\), eine Nullstelle \((k = \pm 1)\) oder keine Nullstelle \((k \in \; ]-\infty;-1[ \cup ]1;+\infty[)\). Der Parameter \(k\) beeinflusst die Anzahl und die Lage der Nullstellen von \(f_{k}\).
b) \(f_{k}(x) = \sin{(x + k)}; \; D_{f_{k}} = \mathbb R, \; k \in \; ]-2\pi;2\pi[, \; k \neq 0\)
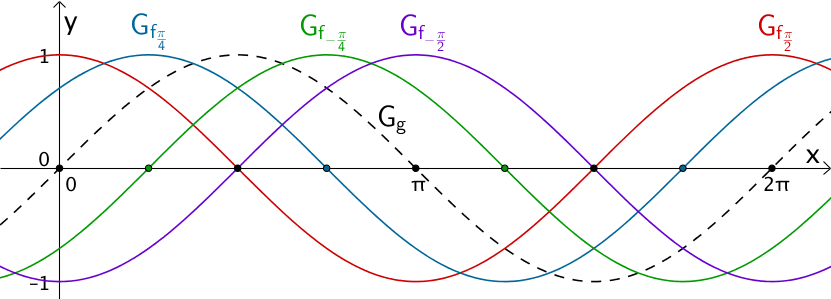
Die Graphen \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto \sin{(x + k)}\) besitzen für jeden Wert des Parameters \(k \in \; ]-2\pi;2\pi[, \; k \neq 0\) im Intervall \([0;2\pi]\) genau zwei Nullstellen, die nicht die Nullstellen der Sinusfunktion \(g\) sind. Der Parameter \(k\) beeinflusst die Lage der Nullstellen von \(f_{k}\).
c) \(f_{k}(x) = \sin{(kx)}; D_{f_{k}} = \mathbb R, \; k \in \mathbb R \backslash \{0\}, \; k > 1\)
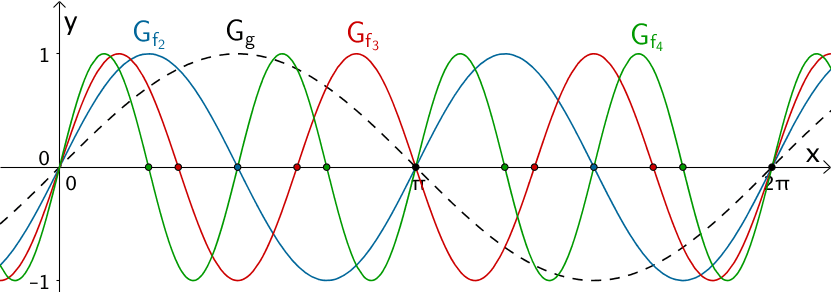
Die Graphen \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto \sin{kx}\) besitzen für \(k > 1\) beliebig viele Nullstellen im Intervall \([0;2\pi]\). Die Nullstellen der Sinusfunktion \(g\) können, müssen aber nicht enthalten sein. Der Parameter \(k\) beeinflusst die Anzahl und die Lage der Nullstellen von \(f_{k}\).
d) \(f_{k}(x) = k \cdot \sin{x}; \, D_{f_{k}} = \mathbb R, \; k \in \mathbb R \backslash \{0\}\)
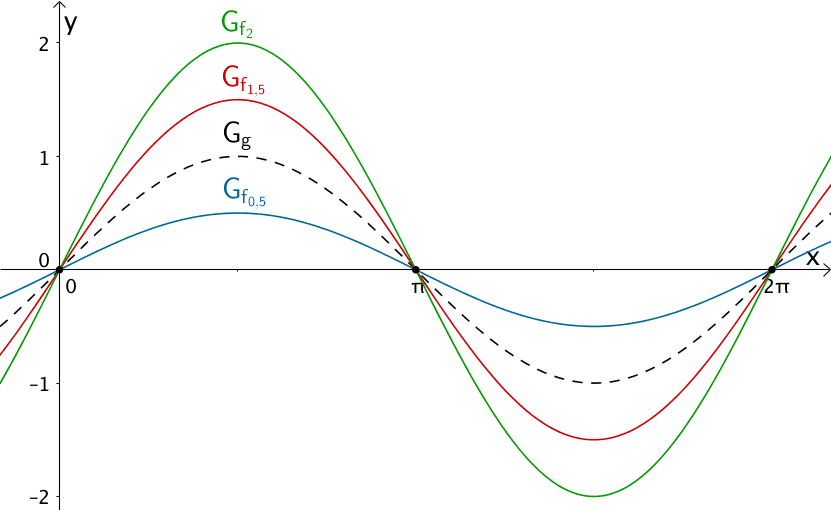
Die Graphen \(G_{f_{k}}\) der Funktionenschar \(f_{k} \colon x \mapsto \sin{kx}\) besitzen für \(k \in \mathbb R \backslash \{0\}\) die identischen Nullstellen wie die Sinusfunktion \(g\). Der Parameter \(k\) hat keinerlei Einfluss auf die Anzahl bzw. Lage der Nullstellen von \(f_{k}\).
Die geschilderten Fälle zeigen lediglich, dass der Parameter \(k\) einer Funktionenschar \(f_{k}\) mehrheitlich Einfluss auf die Nullstellen von \(f_{k}\) nimmt.
Für ein mathematische Aussage zur Lage bzw. Anzahl und ggf. Art der Nullstellen einer Funktionenschar \(f_{k}\) werden die Nullstellen zunächst in Abhängigkeit des Parameters \(k\) bestimmt, um deren Eigenschaften anschließend genauer zu betrachten.
Beispielaufgabe
Gegeben sei die in \(\mathbb R\) definierte Funktionenschar \(f_{k} \colon x \mapsto \dfrac{4}{5}x^{3} - \dfrac{1}{5}x^{2}(8 + 3k) + \dfrac{1}{5}x(6k - k^{2}) + \dfrac{2}{5}k^{2}\) mit \(k \in \mathbb R^{+}\).
Bestimmen Sie den Wert des Parameters \(k\) so, dass der zugehörige Graph der Funktionenschar \(f_{k}\) an der Stelle \(x = 2\) eine doppelte Nullstelle besitzt.
\[f_{k}(x) = \frac{4}{5}x^{3} - \frac{1}{5}x^{2}(8 + 3k) + \frac{1}{5}x(6k - k^{2}) + \frac{2}{5}k^{2}; \; D_{f_{k}} = \mathbb R, \; k \in \mathbb R^{+}\]
Der Graph der ganzrationalen Funktionenschar \(f_{k}\) besitzt an der Stelle \(x = 2\) eine doppelte Nullstelle, wenn die \(x\)-Achse an der Stelle \(x = 2\) waagrechte Tangente an den Graphen ist (vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Vielfachheit von Nullstellen).
Es muss demnach gelten:
\[f_{k}(2) = 0\]
\[f'_{k}(2) = 0\]
Zunächst werden die möglichen Werte für den Parameter \(k\) mithilfe der Bedingung \(f'_{k}(2) = 0\) bestimmt. Anschließend erfolgt die Prüfung, ob die Parameterwerte die Bedingung \(f_{k}(2)\) erfüllen.
Erste Ableitung \(f'_{k} \)bilden:
Die Ableitung des Funktionsterms \(f_{k}(x)\) lässt sich mithilfe der Faktorregel, der Summenregel und der Ableitung einer Potenzfunktion bilden. Der Parameter \(k\) wird dabei wie eine Konstante behandelt (vgl. Abiturskript - 1.5.2 Ableitungsregeln).
\[f_{k}(x) = \frac{4}{5}x^{3} - \frac{1}{5}x^{2}(8 + 3k) + \frac{1}{5}x(6k - k^{2}) + \frac{2}{5}k^{2}\]
\[\begin{align*} f'_{k}(x) &= \frac{4}{5} \cdot 3 \cdot x^{2} - \frac{1}{5} \cdot 2 \cdot x (8 + 3k) + \frac{1}{5}(6k - k^{2}) + 0 \\[0.8em] &= \frac{12}{5}x^{2} - \frac{2}{5}x(8 + 3k) + \frac{1}{5}(6k - k^{2}) \end{align*}\]
Parameterwerte für \(k\) mithilfe der Bedingung \(f'_{k}(2) = 0\) bestimmen:
\[\begin{align*} f'_{k}(2) &= 0 \\[0.8em] \frac{12}{5} \cdot 2^{2} - \frac{2}{5} \cdot 2 \cdot (8 + 3k) + \frac{1}{5}(6k - k^{2}) &= 0 \\[0.8em] \frac{48}{5} - \frac{4}{5}(8 + 3k) + \frac{1}{5}(6k - k^{2}) &= 0 & &| \cdot 5 \\[0.8em] 48 - 4(8 + 3k) + 6k - k^{2} &= 0 \\[0.8em] 48 - 32 - 12k + 6k - k^{2} &= 0 \\[0.8em] -k^{2} - 6k + 16 &= 0 \end{align*}\]
Lösungsformel für quadratische Gleichungen anwenden (vgl. Abiturskript - 1.1.2 Quadratische Funktion, Lösungsformel für quadratische Gleichungen, vgl. Merkhilfe):
\[\begin{align*} k_{1,2} &= \frac{6 \pm \sqrt{(-6)^{2} - 4 \cdot (-1) \cdot 16}}{2 \cdot (-1)} \\[0.8em] &= \frac{-6 \pm \sqrt{100}}{-2} \\[0.8em] &= \frac{-6 \pm 10}{-2} \\[0.8em] &= -3 \pm 5 & &| \: k \in \mathbb R^{+} \end{align*}\]
\[(k_{1} = -8)\]
\[k_{2} = 2\]
Mit \(k \in \mathbb R^{+}\) (vgl. Angabe) ist \(k = 2\) die einzige Lösung der quadratischen Gleichung.
Funktionsterm der Scharfunktion \(f_{2}\):
\[f_{k}(x) = \frac{4}{5}x^{3} - \frac{1}{5}x^{2}(8 + 3k) + \frac{1}{5}x(6k - k^{2}) + \frac{2}{5}k^{2}\]
\[\begin{align*} f_{2}(x) &= \frac{4}{5}x^{3} - \frac{1}{5}x^{2}(8 + 3 \cdot 2) + \frac{1}{5}x(6 \cdot 2 - 2^{2}) + \frac{2}{5} \cdot 2^{2} \\[0.8em] &= \frac{4}{5}x^{3} - \frac{14}{5}x^{2} + \frac{8}{5}x + \frac{8}{5} \end{align*}\]
Prüfen, ob für \(k = 2\) die Bedingung \(f_{2}(2) = 0\) erfüllt ist:
\[\begin{align*} f_{2}(2) &= \frac{4}{5} \cdot 2^{3} - \frac{14}{5} \cdot 2^{2} + \frac{8}{5} \cdot 2 + \frac{8}{5} \\[0.8em] &= \frac{4}{5} \cdot 8 - \frac{14}{5} \cdot 4 + \frac{8}{5} \cdot 2 + \frac{8}{5} \\[0.8em] &= \frac{32}{5} - \frac{56}{5} + \frac{16}{5} \frac{8}{5} \\[0.8em] &= 0 \end{align*}\]
Schlussfolgerung:
Für \(k = 2\) besitzt der Graph der Scharfunktion \(f_{2}\) an der Stelle \(x = 2\) eine doppelte Nullstelle.
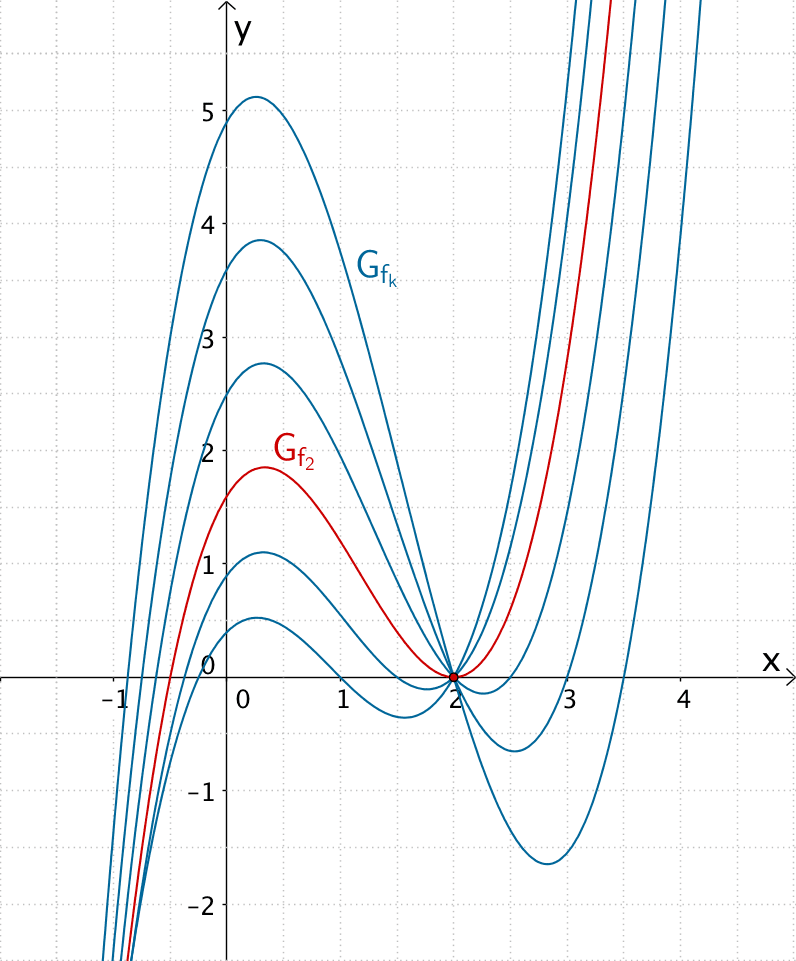
Kurvenschar \(G_{f_{k}}\) der in \(\mathbb R\) definierten Funktionenschar \(f_{k} \colon x \mapsto \dfrac{4}{5}x^{3} - \dfrac{1}{5}x^{2}(8 + 3k) + \dfrac{1}{5}x(6k - k^{2}) + \dfrac{2}{5}k^{2}\) mit \(k \in \mathbb R^{+}\) und Graph \(G_{f_{2}}\) der Scharfunktion \(f_{2}\) mit doppelter Nullstelle \(x = 2\)


