Weisen Sie nach, dass die Gerade \(g\) die Kugel \(K\) im Punkt \(T(3|12|-2)\) berührt.
(5 BE)
Lösung zu Teilaufgabe d
1. Möglichkeit: Berührpunkt mit Kugelgleichung bestimmen
Kugelgleichung in Koordinatendarstellung aufstellen
\(\textcolor{#cc071e}{M(-13|20|0)}\), \(\textcolor{#0087c1}{r = 18}\) (vgl. Teilaufgabe c)
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
\[\begin{align*} &K \colon (x_{1} - \textcolor{#cc071e}{m_{1}})^{2} + (x_{2} - \textcolor{#cc071e}{m_{2}})^{2} + (x_{3} - \textcolor{#cc071e}{m_{3}})^{2} = \textcolor{#0087c1}{r}^{2} \\[0.8em] &K \colon (x_{1} - \textcolor{#cc071e}{(-13)})^{2} + (x_{2} - \textcolor{#cc071e}{20})^{2} + (x_{3} - \textcolor{#cc071e}{0})^{2} = \textcolor{#0087c1}{18}^{2} \\[0.8em] &K \colon (x_{1} + 13)^{2} + (x_{2} - 20)^{2} + x_{3}^{2} = 18^{2} \end{align*}\]
Gemeinsame Punkte der Geraden \(g\) und der Kugel \(K\) berechnen
Hierfür werden die Koordinaten des Ortsvektors \(X\) der Gleichung der Geraden \(g\) in die Gleichung der Kugel \(K\) eingesetzt und diese nach dem Parameter \(\lambda\) aufgelöst.
\[\begin{align*} g \colon \overrightarrow{X} &= \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix}, \; \lambda \in \mathbb R \\[0.8em] g \colon \overrightarrow{X} &= \begin{pmatrix} \textcolor{#89ba17}{3 + 5\lambda} \\ \textcolor{#89ba17}{12 + 11\lambda} \\ \textcolor{#89ba17}{-2 - 4\lambda} \end{pmatrix}, \; \lambda \in \mathbb R \end{align*}\]
\[K \colon (x_{1} + 13)^{2} + (x_{2} - 20)^{2} + x_{3}^{2} = 18^{2}\]
\[\begin{align*} g \cap K \colon (\textcolor{#89ba17}{3 + 5\lambda} + 13)^{2} + (\textcolor{#89ba17}{12 + 11\lambda} - 20)^{2} + (\textcolor{#89ba17}{-2 - 4\lambda})^{2} &= 18^{2} \\[0.8em] (16 + 5\lambda)^{2} + (-8 + 11\lambda)^{2} + (-2 - 4\lambda)^{2} &= 18^{2} \\[0.8em] 256 + 160\lambda + 25\lambda^{2} + 64 - 176 + 121\lambda^{2} + 4 + 16\lambda + 16\lambda^{2} &= 18^{2} \\[0.8em] 162\lambda^{2} + 324 &= 18^{2} \\[0.8em] 162\lambda^{2} + 324 &= 324 &&| - 324 \\[0.8em] 162\lambda^{2} &= 0 &&| : 162 \\[0.8em] \lambda^{2} &= 0 &&| \; \sqrt{\quad} \\[0.8em] \lambda &= 0\end{align*}\]
Da die quadratische Gleichung nur die eine Lösung \(\lambda = 0\) hat, hat die Gerade \(g\) und die Kugel \(K\) genau einen gemeinsamen Punkt, also einen Berührpunkt.
In die Gleichung von \(g\) eingesetzt, liefert der Parameterwert \(\textcolor{#89ba17}{\lambda = 0}\) den Ortsvektor \(T\) des Berührpunktes \(T\).
\[T \in g \colon \, \overrightarrow{T} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \textcolor{#89ba17}{0} \cdot \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix}\]
\(\Rightarrow \enspace T(3|12|-2)\) (Aufpunkt von \(g\) ist Berührpunkt von \(g\) und \(K\))
2. Möglichkeit: Bedingung \(r = \overline{MT}\) anwenden
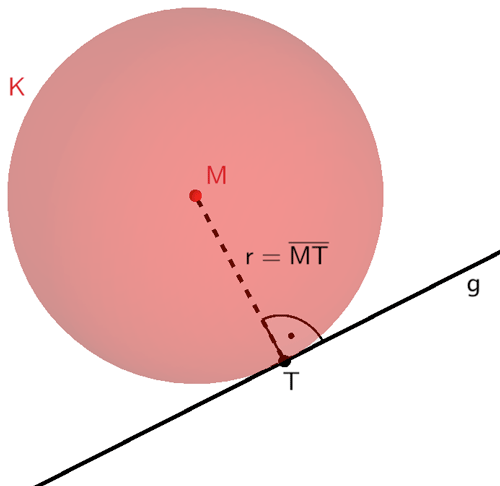
Ist \(T\) ein gemeinsamer Punkt (Berührpunkt oder Schnittpunkt) der Geraden \(g\) und der Kugel \(K\), so gilt für den Kugelradius: \(r = \overline{MT} = 18\) (vgl. Teilaufgabe c).
Der Punkt \(T\) kann allgemein als Punkt der Geraden \(g\) beschrieben werden.
\[T \in g \colon \, \overrightarrow{T} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix} = \begin{pmatrix} \textcolor{#89ba17}{3 + 5\lambda} \\ \textcolor{#89ba17}{12 + 11\lambda} \\ \textcolor{#89ba17}{-2 - 4\lambda} \end{pmatrix}\]
Damit lässt sich die Bedingung \(r = \overline{MT} = \vert \overrightarrow{MT} \vert = 18\) formulieren. Es ergibt sich ein quadratische Gleichung für den Parameter \(\lambda\).
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} r &= 18 \\[0.8em] \overline{MT} &= 18 \\[0.8em] \vert \overrightarrow{MT} \vert &= 18 \\[0.8em] \vert \overrightarrow{T} - \overrightarrow{M} \vert &= 18 \\[0.8em] \left| \begin{pmatrix} \textcolor{#89ba17}{3 + 5\lambda} \\ \textcolor{#89ba17}{12 + 11\lambda} \\ \textcolor{#89ba17}{-2 - 4\lambda} \end{pmatrix} - \begin{pmatrix} -13 \\ 20 \\ 0 \end{pmatrix} \right| &= 18 \\[0.8em] \left| \begin{pmatrix} 16 + 5\lambda \\ -8 + 11\lambda \\ -2 - 4\lambda \end{pmatrix} \right| &= 18 \\[0.8em] \sqrt{(16 + 5\lambda)^{2} + (-8 + 11\lambda)^{2} + (-2 - 4\lambda)^{2}} &= 18 &&|\; (\dots)^{2}\; \text{(Quadrieren)} \\[0.8em] (16 + 5\lambda)^{2} + (-8 + 11\lambda)^{2} + (-2 - 4\lambda)^{2} &= 18^{2} \\[0.8em]256 + 160\lambda + 25\lambda^{2} + 64 - 176 + 121\lambda^{2} + 4 + 16\lambda + 16\lambda^{2} &= 18^{2} \\[0.8em] 162\lambda^{2} + 324 &= 18^{2} \\[0.8em] 162\lambda^{2} + 324 &= 324 &&| - 324 \\[0.8em] 162\lambda^{2} &= 0 &&| : 162 \\[0.8em] \lambda^{2} &= 0 &&| \; \sqrt{\quad} \\[0.8em] \lambda &= 0\end{align*}\]
Da die quadratische Gleichung nur die eine Lösung \(\lambda = 0\) hat, hat die Gerade \(g\) und die Kugel \(K\) genau einen gemeinsamen Punkt, also einen Berührpunkt.
In die Gleichung von \(g\) eingesetzt, liefert der Parameterwert \(\textcolor{#89ba17}{\lambda = 0}\) den Ortsvektor \(T\) des Berührpunktes \(T\).
\[T \in g \colon \, \overrightarrow{T} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \textcolor{#89ba17}{0} \cdot \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix}\]
\(\Rightarrow \enspace T(3|12|-2)\) (Aufpunkt von \(g\) ist Berührpunkt von \(g\) und \(K\))

