Ein grüner Würfel und ein roter Würfel werden gleichzeitig geworfen. Die Zufallsgröße \(X\) beschreibt die Summe der beiden geworfenen Augenzahlen. Geben Sie alle Werte an, die die Zufallsgröße \(X\) annehmen kann, und bestimmen Sie die Wahrscheinlichkeit \(P(X = 7)\).
(3 BE)
Lösung zu Teilaufgabe b
Alle Werte der Zufallsgröße \(X\)
\[x_{i} = \{2; 4; 7; 9; 12\}\]
Begründung (nicht verlangt)
grüner Würfel: 5 Seitenflächen mit Augenzahl 1, eine Seitenfläche mit Augenzahl 6
roter Würfel: je 2 Seitenflächen mit den Augenzahlen 1, 3 bzw. 6
Zufallsgröße \(X\): Summe der beiden geworfenen Augenzahlen
Das vorliegende Zufallsexperiment „Ein grüner Würfel und ein roter Würfel werden gleichzeitig geworfen" lässt sich als zweistufiges Zufallsexperiment auffassen. Die 1. Stufe betrachtet die Augenzahl des grünen Würfels, die zweite Stufe die Augenzahl des roten Würfels (oder umgekehrt).
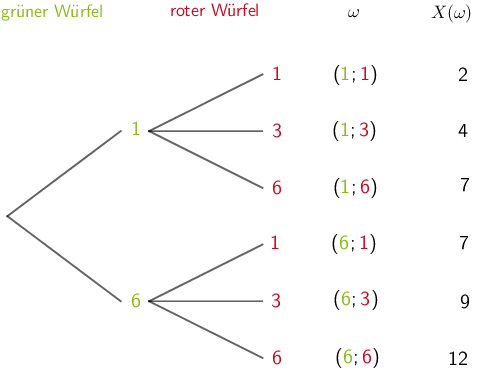
Veranschaulichung mithilfe eines Baumdiagramms
\[\Longrightarrow \quad x_{i} = \{2; 4; 7; 9; 12\}\]
Bestimmung der Wahrscheinlichkeit \(P(X = 7)\)
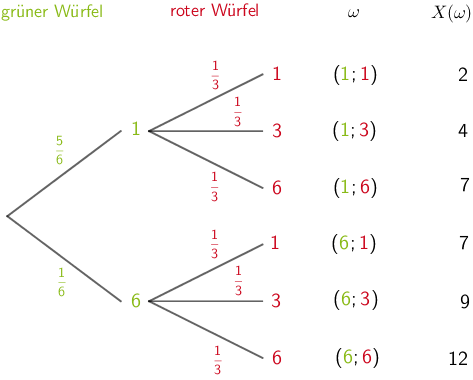
Veranschaulichung mithilfe eines Baumdiagramms
Mithilfe der ersten und der zweiten Pfadregel ergibt sich:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*} P(X = 7) &= \underbrace{P(\textcolor{#89ba17}{1};\textcolor{#cc071e}{6}) + P(\textcolor{#89ba17}{6};\textcolor{#cc071e}{1})}_{\large{\text{2. Pfadregel}}} \\[0.8em] &= \underbrace{\textcolor{#89ba17}{\frac{5}{6}} \cdot \textcolor{#cc071e}{\frac{1}{3}}}_{\large{\text{1. Pfadregel}}} + \underbrace{\textcolor{#89ba17}{\frac{1}{6}} \cdot \textcolor{#cc071e}{\frac{1}{3}}}_{\large{\text{1. Pfadregel}}} \\[0.8em] &= \frac{5}{18} + \frac{1}{18} \\[0.8em] &= \frac{6}{18} \\[0.8em] &= \frac{1}{3}\end{align*}\]

