Für den in Aufgabe 3c bestimmten Wert von \(k\) zeigt Abbildung 3 den zugehörigen Graphen mit seiner Wendetangente. In diesem Koordinatensystem sind die beiden Achsen unterschiedlich skaliert.
Bestimmen Sie die fehlenden Zahlenwerte an den Markierungsstrichen der \(y\)-Achse mithilfe eines geeigneten Steigungsdreiecks an der Wendetangente und tragen Sie die Zahlenwerte in Abbildung 3 ein.
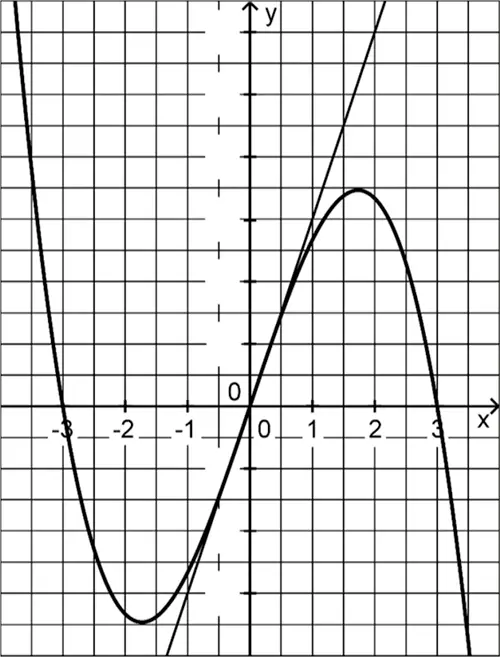Abb. 3
(2 BE)
Lösung zu Teilaufgabe 3d
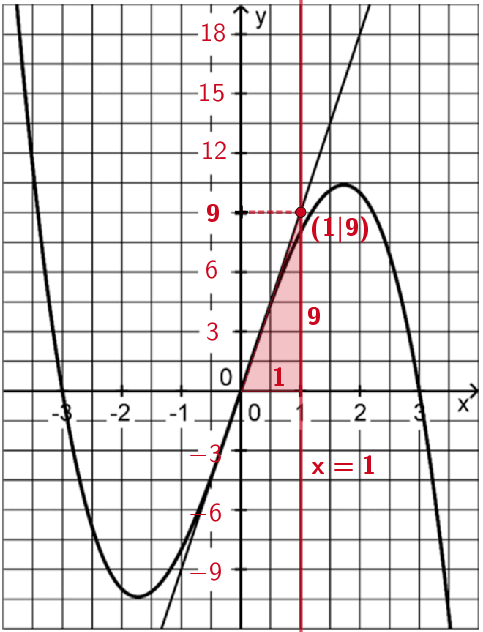
Aufgrund der Steigung der Wendetangente \(m_{W_{-1}} = 9 = \dfrac{9}{1} \left( = \dfrac{\Delta y}{\Delta x}\right)\) (vgl. Teilaufgabe 3c) hat ein vom Koordinatenursprung ausgehendes geeignetes Steigungsdreieck die Seitenlänge \(\textcolor{#cc071e}{1}\).
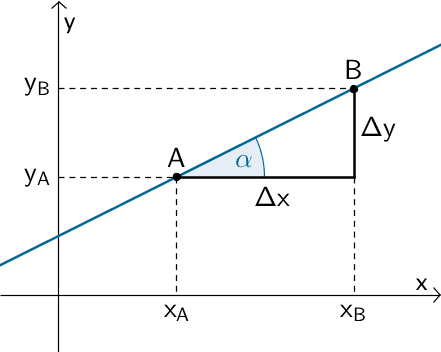
Steigung \(m\) einer Gerade
\[m = \frac{\Delta y}{\Delta x} = \frac{y_B - y_A}{x_B - x_A}\]
\[m = \tan \alpha \quad (\alpha \neq 90^{\circ})\]
Die Gerade mit der Gleichung \(\textcolor{#cc071e}{x = 1}\) schneidet die Wendetangente im Punkt \(\textcolor{#cc071e}{(1|9)}\). Somit kann am dritten positiven Markierungsstrich der \(y\)-Achse der Zahlenwert \(\textcolor{#cc071e}{9}\) eingetragen werden. Die übrigen Zahlenwerte ergeben sich entsprechend der nun bekannten Skalierung: 1 Markierungsstrich der \(y\)-Achse entspricht 3 Längeneinheiten.
