Jeweils zwei benachbarte Zeltwände schließen im Inneren des Zelts einen stumpfen Winkel ein. Ermitteln Sie die Größe dieses Winkels.
(3 BE)
Lösung zu Teilaufgabe c
Schnittwinkel zweier Ebenen
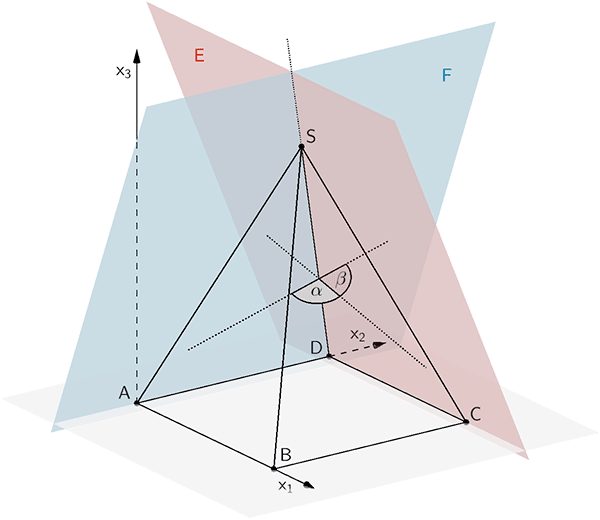
Stumpfer Winkel \(\alpha\), den die Ebene \(E\) (Dreieck \(CDS\)) und die Ebene \(F\) (Dreieck \(DAS\)) stellvertretend für zwei benachbarte Zeltwände im Innern des Zelts (Pyramide \(ABCDS\)) einschließen. Schnittwinkel \(\beta\) der Ebenen \(E\) und \(F\)
Der Schnittwinkel der Ebenen \(E\) und \(F\) ist der spitze Winkel zwischen zwei Geraden, welche in demselben Punkt auf der Schnittgerade senkrecht stehen und in der Ebene \(E\) bzw. in der Ebene \(F\) liegen.
Dieser Schnittwinkel ist gleich dem spitzen Winkel, den die Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) festlegen (Zur besseren Übersicht nicht eingezeichnet).
Der stumpfe Winkel \(\alpha\) ergibt sich als Suplementärwinkel zum Schnittwinkel \(\beta\) (Ergänzungswinkel zu 180°).
\[\alpha = 180^{\circ} - \beta\]
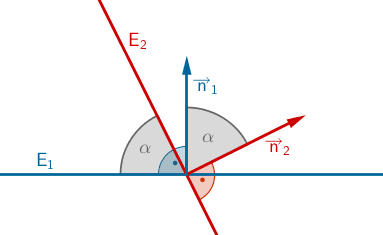
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[E_1\colon \enspace \overrightarrow{n}_1 \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[E_2\colon \enspace \overrightarrow{n}_2 \circ \left( \overrightarrow{X} - \overrightarrow{B} \right) = 0\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_1 \circ \overrightarrow{n}_2 \vert}{\vert \overrightarrow{n}_1 \vert \cdot \vert \overrightarrow{n}_2 \vert} \enspace \Rightarrow \enspace \alpha = \cos^{-1}(\dots)\]
\[(0^{\circ} \leq \alpha \leq 90^{\circ})\]
Die Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) können den Ebenengleichungen entnommen werden (vgl. Angabe und Teilaufgabe b).
Ebenengleichung in Normalenform (vgl. Merkhilfe)
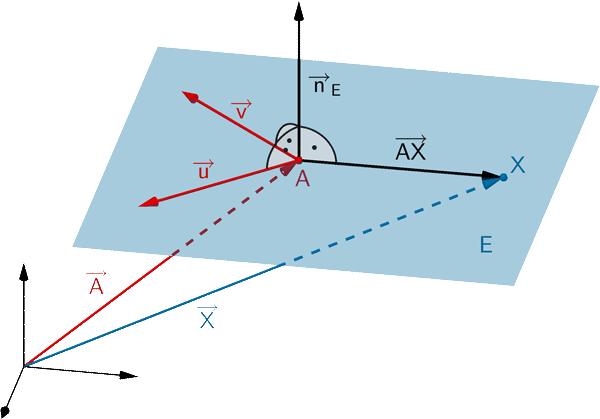
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[E \colon 12x_{2} + 5x_{3} = 60 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 0 \\ 12 \\ 5 \end{pmatrix}\]
\[F \colon 12x_{1} - 5x_{3} = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{F} = \begin{pmatrix} 12 \\ 0 \\ -5 \end{pmatrix}\]
Schnittwinkel \(\beta\) der Ebenen \(E\) und \(F\) berechnen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \cos \beta &= \frac{\left| \overrightarrow{n}_{E} \circ \overrightarrow{n}_{F} \right|}{\left| \overrightarrow{n}_{E} \right| \cdot \left| \overrightarrow{n}_{F} \right|} \\[0.8em] &= \frac{\left| \begin{pmatrix} 0 \\ 12 \\ 5 \end{pmatrix} \circ \begin{pmatrix} 12 \\ 0 \\ -5 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0 \\ 12 \\ 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 12 \\ 0 \\ -5 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert 0 \cdot 12 + 12 \cdot 0 + 5 \cdot (-5) \vert}{\sqrt{0^{2} + {12}^{2} + 5^{2}} \cdot \sqrt{{12}^{2} + 0^{2} + (-5)^{2}}} \\[0.8em] &= \frac{\vert -25 \vert}{\sqrt{169} \cdot \sqrt{169}} \\[0.8em] &= \frac{25}{169} & &| \; \text{TR:} \; \cos^{-1}(\dots) \\[3.2em] \beta &\approx 81{,}48^{\circ}\end{align*}\]
Stumpfen Winkel \(\alpha\) berechnen:
\[\alpha = 180^{\circ} - \beta = 180^{\circ} - 81{,}49^{\circ} = 98{,}51^{\circ}\]
Jeweils zwei benachbarte Zeltwände schließen im Innern des Zelts einen stumpfen Winkel von ca. 98,51° ein.

