Die Windkraftgegner schließen sich zu einer Bürgerinitiative zusammen.
Zur Verbesserung ihrer finanziellen Mittel hat die Bürgerinitiative auf dem Gemeindefest ein Glücksrad mit zehn gleich großen Sektoren aufgebaut (vgl. Abbildung). Ein Spiel besteht aus dem einmaligen Drehen des Glücksrads; die erzielte Zahl gibt die Kategorie des Preises an, den der Spieler erhält.
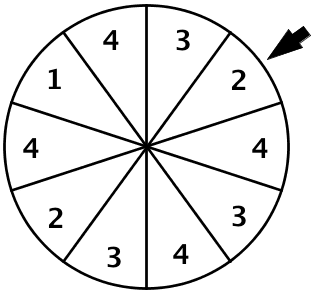
Ein Preis der Kategorie 1 ist für die Bürgerinitiative mit Unkosten in Höhe von zehn Euro, ein Preis der Kategorie 2 mit Unkosten in Höhe von fünf Euro verbunden. Preise der Kategorie 3 und 4 werden von Sponsoren gestellt und verursachen keine Unkosten. Bestimmen Sie den im Mittel pro Spiel zu erwartenden Gewinn der Bürgerinitiative, wenn der Einsatz für ein Spiel 2,50 Euro beträgt und keine weiteren Unkosten anfallen.
(5 BE)
Lösung zu Teilaufgabe 2a
Die Wahrscheinlichkeiten der Preiskategorien sind gegeben mit:
\[P(\text{1}) = \frac{1}{10} =0{,}1\,;\quad P(\text{2}) = \frac{2}{10} =0{,}2\,;\]
\[P(\text{3}) = \frac{3}{10} =0{,}3\,;\quad P(\text{4}) = \frac{4}{10} =0{,}4\,;\]
Erwartungswert des Gewinns \(G\) pro Spiel
Die Zufallsgröße \(G\) ordnet jeder Preiskategorie einen Gewinn \(g_i\) in Euro zu.
Gewinn \(G\) = "Einsatz minus Unkosten"
Einsatz pro Spiel: 2,50 €
| Preiskategorie | \(1\) | \(2\) | \(3\) | \(4\) |
| Unkosten [€] | \(10\) | \(5\) | \(0\) | \(0\) |
| \(g_i\) [€] | \(-7{,}50\) | \(-2{,}50\) | \(2{,}50\) | \(2{,}50\) |
| \(P(G = g_i)\) | \(0{,}1\) | \(0{,}2\) | \(0{,}3\) | \(0{,}4\) |
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) der Zufallsgröße \(\boldsymbol{X}\) (vgl. Merkhilfe)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot p_{i} \\[0.8em] &= x_{1} \cdot p_{1} + x_{2} \cdot p_{2} \,+\, ... \,+\, x_{n} \cdot p_{n} \end{align*}\]
Der Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(X\) gibt den Mittelwert der Zufallsgröße an, der bei oftmaliger Wiederholung eines Zufallsexperiments zu erwarten ist.
\[\begin{align*} E(G) &= \sum \limits_{i\;=\;1}^{4} g_i \cdot P(G = g_i) \\[0.8em] &= g_1 \cdot P(G = g_1) + g_2 \cdot P(G = g_2) + g_3 \cdot P(G = g_3) + g_4 \cdot P(G = g_4) \\[0.8em] &= (-7{,}50 \cdot 0{,}1 - 2{,}50 \cdot 0{,}2 + 2{,}50 \cdot 0{,}3 + 2{,}50 \cdot 0{,}4) \, \text{€} \\[0.8em] &= 0{,}50\;\text{€} \end{align*}\]
Der im Mittel zu erwartenden Gewinn pro Spiel beträgt 0,50 €.


