Bestimmen Sie die Wahrscheinlichkeiten folgender Ereignisse.
\(A\): „Das fünfte ausgewählte Auto ist das erste mit ESP."
\(B\): „Die Zufallsgröße \(X\) nimmt einen Wert an, der von ihrem Erwartungswert höchstens um eine Standardabweichung abweicht."
(7 BE)
Lösung zu Teilaufgabe 1b
Binomialverteilung, binomialverteilte Zufallsgröße, Erwartungswert und Standardabweichung einer binomialverteilten Zufallsgröße
Wahrscheinlichkeit des Ereignisses \(A\)
\(A\): „Das fünfte ausgewählte Auto ist das erste mit ESP."
Das Ereignis \(A\) bedeutet, die ersten vier ausgewählten Autos sind nicht mit ESP ausgerüstet und das fünfte ausgewählte Auto ist mit ESP ausgerüstet. Über die verbleibenden 195 zufällig ausgewählten Autos liegt keine Aussage vor. Deshalb sind diese für die Berechnung der Wahrscheinlichkeit des Ereignisses \(A\) nicht von Bedeutung.
Die Wahrscheinlichkeit für das Ereignis „Ein zufällig ausgerüstetes Auto ist mit ESP ausgerüstet" ist mit \(p = 0{,}4\) konstant (vgl. Angabe, Teilaufgabe 1a). Die Wahrscheinlichkeit für das Gegenereignis „Ein zufällig ausgewähltes Auto ist nicht mit ESP ausgerüstet" ist mit \(1 - p = 1 - 0{,}4 = 0{,}6\) ebenfalls konstant.
\[P(A) = 0{,}6^{4} \cdot 0{,}4 = 0{,}05184 \approx 5{,}2\,\%\]
Anmerkung:
Zwar ist die Wahrscheinlichkeit für das Ereignis „Ein zufällig ausgewähltes Auto ist mit ESP ausgerüstet" mit \(p = 0{,}4\) konstant (Urnenmodell: „Ziehen mit Zurücklegen"), doch nennt die Aufgabenstellung die Reihenfolge für das Eintreten des Ereignisses.
Deshalb kann die Wahrscheinlichkeit \(P(A)\) nicht mithilfe des Terms \(\displaystyle \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k}\) berechnet werden. Der Binomialkoeffizient \(\displaystyle \binom{n}{k} = \binom{5}{1} = 5\) würde fünf mögliche Reihenfolgen berücksichtigen, welches der nacheinander ausgewählten Autos mit ESP ausgerüstet ist.
Wahrscheinlichkeit des Ereignisses \(B\)
\(B\): „Die Zufallsgröße \(X\) nimmt einen Wert an, der von ihrem Erwartungswert höchstens um eine Standardabweichung abweicht."
Zufallsgröße \(X\): Anzahl der ausgewählten Autos mit ESP (vgl. Angabe)
\(n = 200\), \(p = 0{,}4\)
Die Zufallsgröße \(X\) ist nach \(B(200;0{,}4)\) binomialverteilt (vgl. Teilaufgabe 1a).
Die Standardabweichung \(\sigma\) ist eine Maßzahl für die Streuung der Werte \(x_{i}\) der Zufallsgröße \(X\) um ihren Erwartungswert \(\mu\). Streuen die Werte der Zufallsgröße \(X\) um höchstens eine Standardabweichung, kann die Zufallsgröße \(X\) Werte aus dem Intervall \([\mu - \sigma;\mu + \sigma]\) annehmen, wobei \(x_{i} \in \{0, 1, \dots, 200\}\) gilt.
Gesucht ist also folgende Wahrscheinlichkeit:
\[P_{0{,}4}^{200}(\mu - \sigma \leq X \leq \mu + \sigma)\]
Eine etwas ausführlichere mathematische Betrachtung der Fragestellung sei als Alternative ebenfalls angeführt.
Abweichung des Wertes der Zufallsgröße \(X\) von ihrem Erwartungswert \(\mu\):
\[\vert X - \mu \vert\]
Diese Abweichung soll höchstens eine Standardabweichung \(\sigma\) betragen, wobei die Zufallsgröße \(X\) Werte \(x_{i} < \mu\) oder \(x_{i} > \mu\) annehmen kann.
\[\Longrightarrow \quad \vert X - \mu \vert \leq \sigma\]
\[\vert X - \mu \vert = \left\{ \begin{align*} &X - \mu \enspace \text{für} \enspace x_{i} > \mu \\[0.8em] &\mu - X \enspace \text{für} \enspace x_{i} < \mu \end{align*} \right.\]
Damit ergeben sich die beiden folgenden Bedingungen:
Für \(x_{i} > \mu\):
\[\begin{align*}X - \mu &\leq \sigma & &| + \mu \\[0.8em] X &\leq \mu + \sigma \end{align*}\]
Für \(x_{i} < \mu\):
\[\begin{align*}\mu - X &\leq \sigma & &| + X - \sigma \\[0.8em] \mu - \sigma &\leq X \end{align*}\]
\[\Longrightarrow \quad \mu - \sigma \leq X \leq \mu + \sigma\]
Gesucht ist also folgende Wahrscheinlichkeit:
\[P_{0{,}4}^{200}(\vert X - \mu \vert \leq \sigma) = P_{0{,}4}^{200}(\mu - \sigma \leq X \leq \mu + \sigma)\]
Erwartungswert \(\mu\) der binomialverteilten Zufallsgröße \(X\) berechnen:
Erwartungswert \(\boldsymbol{\mu}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\(\mu = E(X) = n \cdot p\) (vgl. Merkhilfe)
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
\(n = 200\), \(p = 0{,}4\)
\[\mu = E(X) = n \cdot p = 200 \cdot 0{,}4 = 80\]
Standardabweichung \(\sigma\) der binomialverteilten Zufallsgröße \(X\) berechnen:
Standardabweichung \(\boldsymbol{\sigma}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\[\sigma = \sqrt{Var(X)} = \sqrt{n \cdot p \cdot (1 - p)}\]
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist. \(Var(X)\) bezeichnet die Varianz der Zufallsgröße \(X\).
\(n = 200\), \(p = 0{,}4\)
\[\sigma = \sqrt{n \cdot p \cdot (1 - p)} = \sqrt{200 \cdot 0{,}4 \cdot 0{,}6} = 4\sqrt{3} \approx 6{,}93\]
Grenzen \(\mu - \sigma\) und \(\mu + \sigma\) berechnen:
\(\mu = 80\), \(\sigma = 6{,}93\)
\[\mu - \sigma = 80 - 6{,}93 = 73{,}07\]
\[\mu + \sigma = 80 + 6{,}93 = 86{,}93\]
\[\begin{align*}\Longrightarrow \quad 73{,}07 \leq &X \leq 86{,}93 & &| \; x_{i} \in \{0, 1, \dots, 200\} \\[0.8em] 74 \leq &X \leq 86\end{align*}\]
Wahrscheinlichkeit \(P_{0{,}4}^{200}(\vert X - \mu \vert \leq \sigma)\) berechnen:
Die Wahrscheinlichkeit lässt sich auf die kumulative Verteilungsfunktion zurückführen, sodass das Stochastische Tafelwerk (ST) verwendet werden kann.
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
\[\begin{align*} P_{0{,}4}^{200}(\vert X - \mu \vert \leq \sigma) &= P_{0{,}4}^{200}(\mu - \sigma \leq X \leq \mu + \sigma) \\[0.8em] &= P_{0{,}4}^{200}(74 \leq X \leq 86) \\[0.8em] &= P_{0{,}4}^{200}(X \leq 86) - P_{0{,}4}^{200}(X \leq 73) \\[0.8em]&= \sum \limits_{i\,=\,0}^{86}B(200;0{,}4;i) - \sum \limits_{i\,=\,0}^{73}B(200;0{,}4;i) \\[0.8em] &\overset{\text{ST}}{=} 0{,}82607 - 0{,}17423 \\[0.8em] &= 0{,}65184 \\[0.8em] &\approx 65{,}2\,\% \end{align*}\]
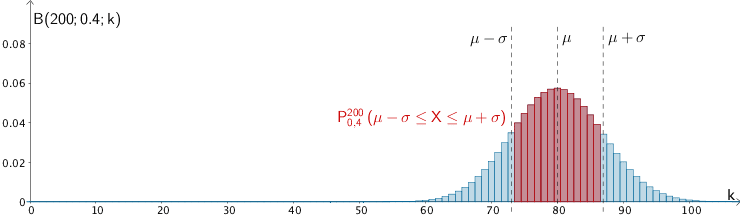
Wahrscheinlichkeitsverteilung der nach \(B(200;0,4)\) binomialverteilten Zufallsgröße \(X\), Wahrscheinlichkeit \(P_{0{,}4}^{200}(\mu - \sigma \leq X \leq \mu + \sigma)\) dafür, dass der Wert der Zufallsgröße \(X\) höchstens um eine Standardabweichung \(\sigma\) von ihrem Erwartungswert \(\mu\) abweicht (verkürzte Darstellung bis \(k = 100\)).


