Zeigen Sie, dass die Größe des Winkels \(\beta\) zwischen reflektiertem Lichtstrahl und Einfallslot mit der Größe des Winkels \(\alpha\) zwischen einfallendem Lichtstrahl und Einfallslot übereinstimmt.
(4 BE)
Lösung zu Teilaufgabe e
Richtungsvektor von \(g\) (einfallender Lichtstrahl): \(\overrightarrow{v} = \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix}\) (siehe Teilaufgabe b)
Richtungsvektor von \(h\) (reflektierter Lichtstrahl): \(\overrightarrow{QR} = \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 0 \end{pmatrix}\) (siehe Teilaufgabe d)
Richtungsvektor des Einfallslots (Normalenvektor der Ebene \(E\)): \(\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}\) (siehe Teilaufgabe c)
Die Größe des Winkels α bzw. β ist gleich der Größe des Winkels zwischen dem Richtungsvektor der Geraden \(g\) bzw. der Geraden \(h\) und dem Richtungsvektor des Einfallslots (Normalenvektor der Ebene \(E\)).
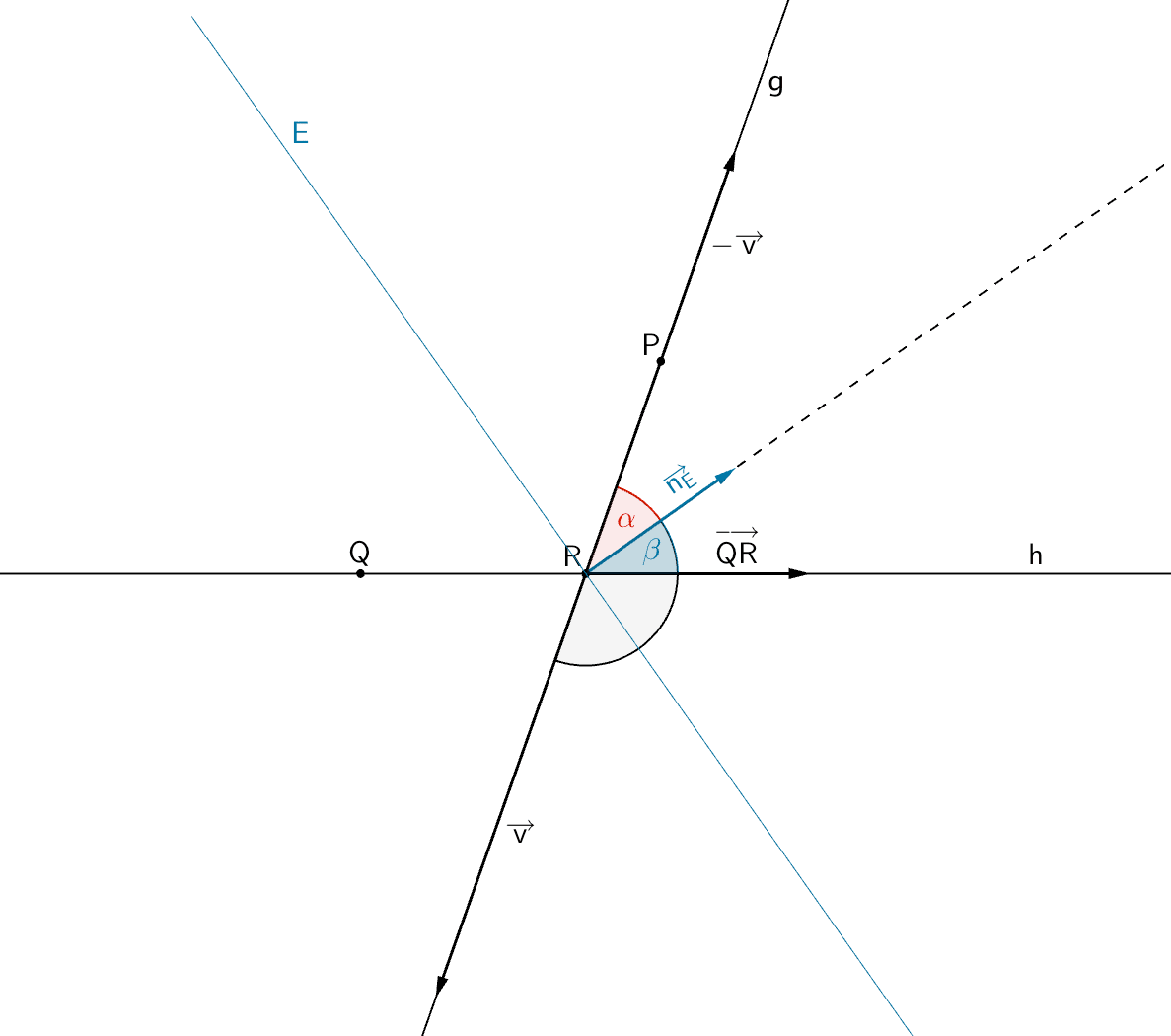
Winkel \(\alpha\) zwischen einfallendem Lichtstrahl (Gerade \(g\)) und Einfallslot, Winkel \(\beta\) zwischen reflektiertem Lichtstrahl (Gerade \(h\)) und Einfallslot
Anwendung des Skalarprodukts:
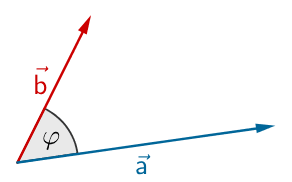
Winkel zwischen zwei Vektoren (vgl. Merkhilfe)
\[\cos \varphi = \frac{\overrightarrow{a} \circ \overrightarrow{b}}{\vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert}\,; \quad \varphi \in [0;\pi]\]
Bei der Berechnung der Größe des Winkels \(\alpha\) muss darauf geachtet werden, dass der Winkel zwischen dem Richtungsvektor \(\overrightarrow{v}\) und dem Normalenvektor \(\overrightarrow{n}_{E}\) in mathematisch positivem Sinn (gegen den Uhrzeigersinn) ein stumpfer Winkel ist.
Um die Größe des spitzen Winkels zu berechnen, wählt man entweder den Gegenvektor \(-\overrightarrow{v}\) oder verwendet die Formel \(\displaystyle \cos{\alpha} = \frac{\vert \overrightarrow{v} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{v} \vert \cdot \vert \overrightarrow{n}_{E} \vert}\). Der Betrag im Zähler bewirkt einen positiven Kosinus und somit einen Winkel zwischen 0° und 90°.
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \cos{\alpha} &= \cos{\beta} \\[0.8em] \frac{\vert \overrightarrow{v} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{v} \vert \cdot \vert \overrightarrow{n}_{E} \vert} &= \frac{\vert \overrightarrow{QR} \circ \overrightarrow{n}_{E} \vert}{\vert \overrightarrow{QR} \vert \cdot \vert \overrightarrow{n}_{E} \vert} \\[0.8em] \frac{\left| \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix} \circ \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \right|}{\left| \begin{pmatrix} -1 \\ -1 \\ -4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \right|} &= \frac{\left| \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 0 \end{pmatrix} \circ \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \right|}{\left| \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 0 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \right|} \\[0.8em] \frac{\vert (-1) \cdot 1 + (-1) \cdot 1 + (-4) \cdot 1 \vert}{\sqrt{(-1)^2 + (-1)^2 + (-4)^2} \cdot \sqrt{1^2 + 1^2 + 1^2}} &= \frac{\vert 1{,}5 \cdot 1 + 1{,}5 \cdot 1 + 0 \cdot 1 \vert}{\sqrt{1{,}5^2 + 1{,}5^2 + 0^2} \cdot \sqrt{1^2 + 1^2 + 1^2}} \\[0.8em] \frac{\vert -6 \vert}{\sqrt{18} \cdot \sqrt{3}} &= \frac{\vert 3 \vert}{\sqrt{4{,}5} \cdot \sqrt{3}} \\[0.8em] \frac{6}{\sqrt{54}} &= \frac{3}{\sqrt{13{,}5}} \\[0.8em] \frac{6}{\sqrt{54}} &= \frac{2 \cdot 3}{2 \cdot \sqrt{13{,}5}} \\[0.8em] \frac{6}{\sqrt{54}} &= \frac{6}{\sqrt{4 \cdot 13{,}5}} \\[0.8em] \frac{6}{\sqrt{54}} &= \frac{6}{\sqrt{54}} \\[0.8em] \frac{6}{\sqrt{9 \cdot 6}} &= \frac{6}{\sqrt{9 \cdot 6}} \\[0.8em] \frac{\sqrt{6}}{3} &= \frac{\sqrt{6}}{3} \end{align*}\]
\[\Longrightarrow \quad \alpha = \beta\]
Anmerkung: Natürlich ist es ebenfalls möglich, die Größe des Winkels \(\alpha\) bzw. \(\beta\) mit \(\displaystyle \cos{\alpha} =\frac{6}{\sqrt{54}}\) bzw. \(\displaystyle \cos{\beta} = \frac{3}{\sqrt{13{,}5}}\) zu berechnen, um zu zeigen, dass die Winkel gleich groß sind.


