Im Folgenden ist \(n = 200\). Die Zufallsgröße \(X\) beschreibt die Anzahl der Personen unter den ausgewählten Personen, die an einer Allergie leiden. Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Wert der binomialverteilten Zufallsgröße \(X\) höchstens um eine Standardabweichung von ihrem Erwartungswert abweicht.
(5 BE)
Lösung zu Teilaufgabe 2b
Binomialverteilung, Erwartungswert und Standardabweichung einer binomialverteilten Zufallsgröße
\(n = 200\), \(p = 0{,}25\)
Zufallsgröße \(X\): Anzahl der Personen unter den ausgewählten Personen, die an einer Allergie leiden.
Die Zufallsgröße \(X\) ist nach \(B(200;0{,}25)\) binomialverteilt.
Die Standardabweichung \(\sigma\) ist eine Maßzahl für die Streuung der Werte \(x_{i}\) der Zufallsgröße \(X\) um ihren Erwartungswert \(\mu\). Streuen die Werte der Zufallsgröße \(X\) um höchstens eine Standardabweichung, kann die Zufallsgröße \(X\) Werte aus dem Intervall \([\mu - \sigma;\mu + \sigma]\) annehmen, wobei \(x_{i} \in \{0, 1, \dots, 200\}\) gilt.
Gesucht ist also folgende Wahrscheinlichkeit:
\[P(\mu - \sigma \leq X \leq \mu + \sigma)\]
Eine etwas ausführlichere mathematische Betrachtung der Fragestellung sei als Alternative ebenfalls angeführt.
Abweichung des Wertes der Zufallsgröße \(X\) von ihrem Erwartungswert \(\mu\):
\[\vert X - \mu \vert\]
Diese Abweichung soll höchstens eine Standardabweichung \(\sigma\) betragen, wobei die Zufallsgröße \(X\) Werte \(x_{i} < \mu\) oder \(x_{i} > \mu\) annehmen kann.
\[\Longrightarrow \quad \vert X - \mu \vert \leq \sigma\]
\[\vert X - \mu \vert = \left\{ \begin{align*} &X - \mu \enspace \text{für} \enspace x_{i} > \mu \\[0.8em] &\mu - X \enspace \text{für} \enspace x_{i} < \mu \end{align*} \right.\]
Damit ergeben sich die beiden folgenden Bedingungen:
Für \(x_{i} > \mu\):
\[\begin{align*}X - \mu &\leq \sigma & &| + \mu \\[0.8em] X &\leq \mu + \sigma \end{align*}\]
Für \(x_{i} < \mu\):
\[\begin{align*}\mu - X &\leq \sigma & &| + X - \sigma \\[0.8em] \mu - \sigma &\leq X \end{align*}\]
\[\Longrightarrow \quad \mu - \sigma \leq X \leq \mu + \sigma\]
Gesucht ist also folgende Wahrscheinlichkeit:
\[P(\vert X - \mu \vert \leq \sigma) = P(\mu - \sigma \leq X \leq \mu + \sigma)\]
Erwartungswert \(\mu\) der binomialverteilten Zufallsgröße \(X\) berechnen:
Erwartungswert \(\boldsymbol{\mu}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\(\mu = E(X) = n \cdot p\) (vgl. Merkhilfe)
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
\(n = 200\), \(p = 0{,}25\)
\[\mu = E(X) = n \cdot p = 200 \cdot 0{,}25 = 50\]
Standardabweichung \(\sigma\) der binomialverteilten Zufallsgröße \(X\) berechnen:
Standardabweichung \(\boldsymbol{\sigma}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\[\sigma = \sqrt{Var(X)} = \sqrt{n \cdot p \cdot (1 - p)}\]
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist. \(Var(X)\) bezeichnet die Varianz der Zufallsgröße \(X\).
\(n = 200\), \(p = 0{,}25\)
\[\sigma = \sqrt{n \cdot p \cdot (1 - p)} = \sqrt{200 \cdot 0{,}25 \cdot 0{,}75} = \frac{5\sqrt{6}}{2} \approx 6{,}12\]
Grenzen \(\mu - \sigma\) und \(\mu + \sigma\) berechnen:
\(\mu = 50\), \(\sigma = 6{,}12\)
\[\mu - \sigma = 50 - 6{,}12 = 43{,}88\]
\[\mu + \sigma = 50 + 6{,}12 = 56{,}12\]
\[\begin{align*}\Longrightarrow \quad 43{,}88 \leq &X \leq 56{,}12 & &| \; x_{i} \in \{0, 1, \dots, 200\} \\[0.8em] 44 \leq &X \leq 56\end{align*}\]
Wahrscheinlichkeit \(P(\vert X - \mu \vert \leq \sigma)\) berechnen:
Die Wahrscheinlichkeit lässt sich auf die kumulative Verteilungsfunktion zurückführen, sodass das Stochastische Tafelwerk (ST) verwendet werden kann.
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
\[\begin{align*} P(\vert X - \mu \vert \leq \sigma) &= P(\mu - \sigma \leq X \leq \mu + \sigma) \\[0.8em] &= P(44 \leq X \leq 56) \\[0.8em] &= P(X \leq 56) - P(X \leq 43) \\[0.8em] &= \sum \limits_{i = 0}^{56}B(200;0{,}25;i) - \sum \limits_{i = 0}^{43}B(200;0{,}25;i) \\[0.8em] &\overset{\text{ST}}{=} 0{,}85546 - 0{,}14376 \\[0.8em] &= 0{,}71170 \\[0.8em] &\approx 71{,}2\,\% \end{align*}\]
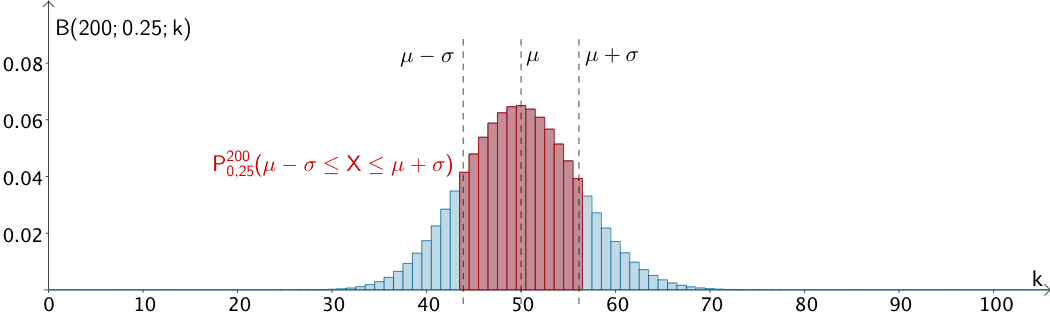
Wahrscheinlichkeitsverteilung der nach \(B(200;0,25)\) binomialverteilten Zufallsgröße \(X\), Wahrscheinlichkeit \(P_{0{,}25}^{200}(\mu - \sigma \leq X \leq \mu + \sigma)\) dafür, dass der Wert der Zufallsgröße \(X\) höchstens um eine Standardabweichung \(\sigma\) von ihrem Erwartungswert \(\mu\) abweicht (verkürzte Darstellung bis \(k = 100\)).

