Berechnen Sie auf der Grundlage des Modells, wie viele Monate nach Beobachtungsbeginn eine Sonnenblume eine Höhe von 1,5 Metern erreicht. Beschreiben Sie, wie man den Wert graphisch überprüfen kann.
(5 BE)
Lösung zu Teilaufgabe 2b
\[f(x) = \frac{2e^x}{e^x + 9}\,; \quad x \in [0;4]\]
\(f(x)\,\): Höhe der Sonnenblume in Metern
\(x\,\): Zeit seit Beobachtungsbeginn in Monaten
Zeit bis die Sonnenblume eine Höhe von 1,5 Metern erreicht
\[\begin{align*}f(x) &= 1{,}5 \\[0.8em] \frac{2e^x}{e^x + 9} &= \frac{3}{2} & &| \cdot 2 \enspace \cdot(e^x + 9) \\[0.8em] 4e^x &= 3(e^x + 9) \\[0.8em] 4e^x &= 3e^x + 27 & &| -3e^x \\[0.8em] e^x &= 27 & &| \; \ln(\dots) \\[0.8em] x &= \ln(27) \\[0.8em] x &= 3\ln(3) \approx 3{,}3\end{align*}\]
Nach ca. 3,3 Monaten seit Beobachtungsbeginn erreicht die Sonnenblume eine Höhe von 1,5 Metern.
Graphische Überprüfung des berechneten Wertes
1. Einzeichnen der Gerade \(y = 1{,}5\)
2. Schnittpunkt von \(G_f\) mit der Geraden \(y = 1{,}5\) bestimmen
3. \(x\)-Koordinate des Schnittpunktes ablesen
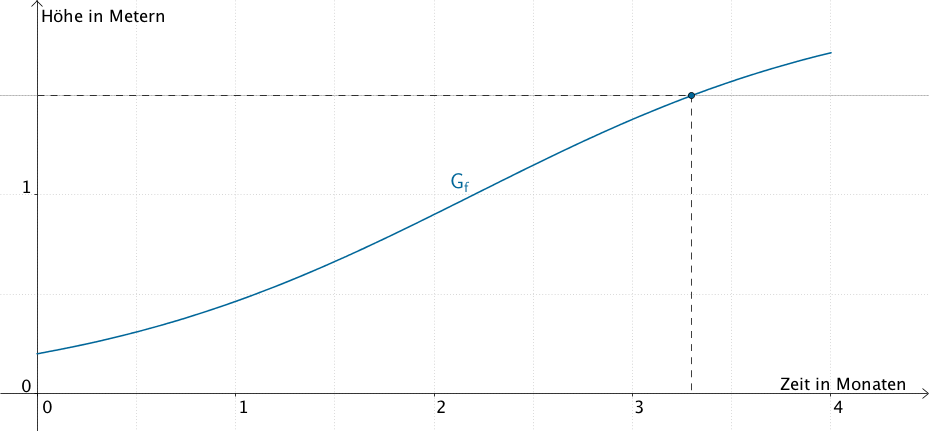
Graphische Überprüfung des berechneten Wertes: \(\;y = 1{,}5 \enspace \longrightarrow \enspace x \approx 3{,}3\)


