Der Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto x \cdot \sin x\) verläuft durch den Koordinatenursprung. Berechnen Sie \(f''(0)\) und geben Sie das Krümmungsverhalten des Graphen von \(f\) in unmittelbarer Nähe des Koordinatenursprungs an.
(4 BE)
Lösung zu Teilaufgabe 2
\[f(x) = x \cdot \sin x\, ; \quad D = \mathbb R\]
Berechnung von \(f''(0)\)
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Ableitung der Sinusfunktion
\[ f(x) = \sin x \quad \Longrightarrow \quad f'(x) = \cos x\]
Ableitung der Kosinusfunktion
\[ f(x) = \cos x \quad \Longrightarrow \quad f'(x) = -\sin x\]
(vgl. Merkhilfe)
\[\begin{align*} f'(x) &= 1 \cdot \sin x + x \cdot \cos x \\[0.8em] &= \sin x + x \cdot \cos x \end{align*}\]
\[\begin{align*} f''(x) &= \cos x + 1 \cdot \cos x + x \cdot (-\sin x) \\[0.8em] &= \cos x + \cos x - x \cdot \sin x \\[0.8em] &= 2\cos x - x \cdot \sin x \end{align*}\]
\[f''(0) = 2 \cdot \underbrace{\cos 0}_{1} - 0 \cdot \sin 0 = 2\]
Krümmungsverhalten von \(G_f\) in unmittelbarer Nähe des Koordinatenursprungs
1. Lösungsansatz: Wert der Zweiten Ableitung \(f''(x)\) in der Nähe von \(x = 0\)
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
\[f''(x) = 2\cos x - x \cdot \sin x\]
Für \(x \to 0\) strebt der Term \(x \cdot \sin x\) gegen Null und der Term \(2 \cos x\) gegen den Wert \(2\).
\[\lim \limits_{x \,\to \, 0^-} f''(x) = \lim \limits_{x \,\to \, 0^-} \; \underbrace{2 \cos x}_{\to \, 2} - \underbrace{x \cdot \sin x}_{\to \, 0} = 2\]
\[\lim \limits_{x \,\to \, 0^+} f''(x) = \lim \limits_{x \,\to \, 0^+} \; \underbrace{2 \cos x}_{\to \, 2} - \underbrace{x \cdot \sin x}_{\to \, 0} = 2\]
Somit gilt in der unmittelbaren Nähe des Koordinatenursprungs:
\(f''(x) > 0 \quad \Longrightarrow \quad G_f\) ist linksgekrümmt.
2. Lösungsansatz: Art des Extrempunkts
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
Wegen \(f'(0) = \sin 0 + 0 \cdot \cos 0 = 0\) und \(f''(0) > 0\) hat \(G_f\) an der Stelle \(x = 0\) ein relatives Minimum. Daraus lässt sich folgern, dass \(G_f\) in unmittelbarer Nähe des Koordinatenursprungs linksgekrümmt ist.
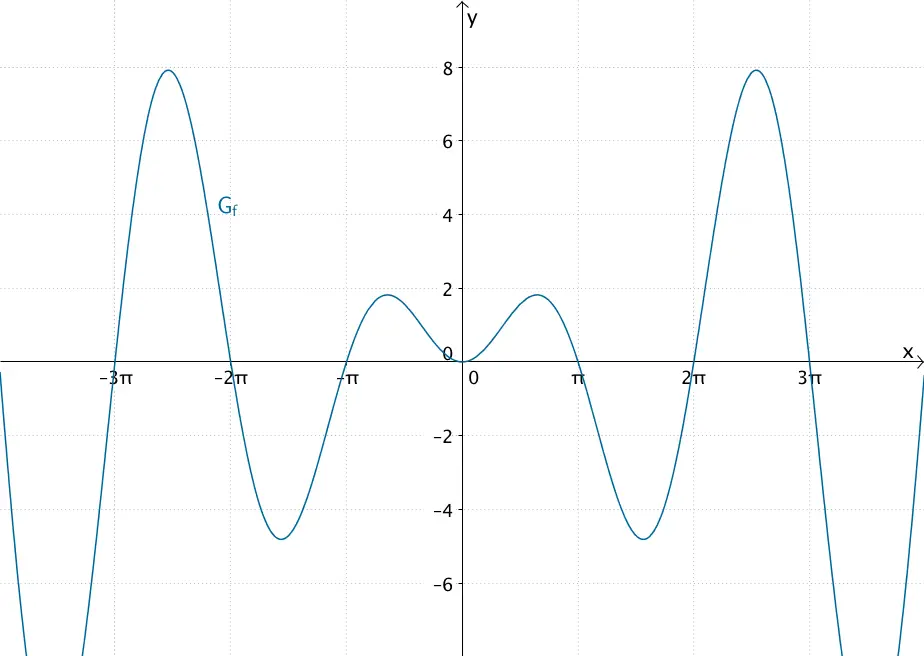
Graph der Funktion \(f\)


