Verschieben von Funktionsgraphen
Verschiebung in \(y\)-Richtung
Der Graph der Funktion \(g\) mit \(g(x) = f(x) + b\) entsteht durch Verschiebung des Graphen der Funktion \(f\) um \(b\) in \(y\)-Richtung.
Verschiebung um \(\boldsymbol{b}\) in \(\boldsymbol{y}\)-Richtung
\[g(x) = f(x) + b\]
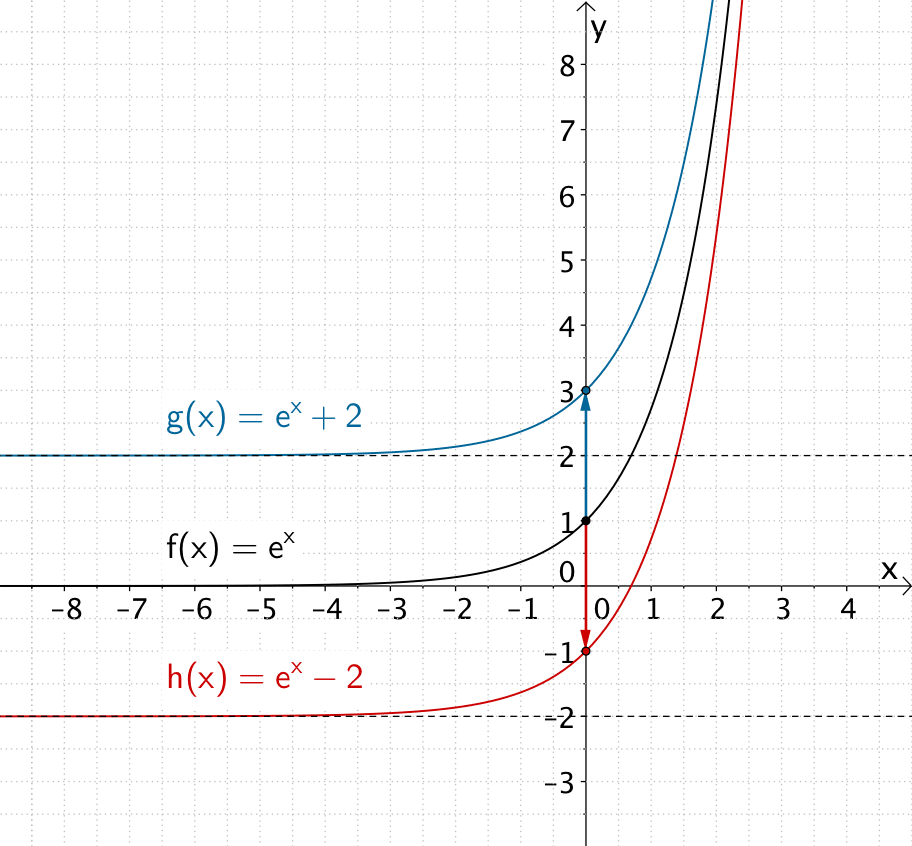
Der Graph der Funktion \(g\) entsteht durch Verschiebung des Graphen der Funktion \(f\) um \(+2\) in \(y\)-Richtung.
Der Graph der Funktion \(h\) entsteht durch Verschiebung des Graphen der Funktion \(f\) um \(-2\) in \(y\)-Richtung.
Verschiebung in \(x\)-Richtung
Der Graph der Funktion \(g\) mit \(g(x) = f(x + a)\) entsteht durch Verschiebung des Graphen der Funktion \(f\) um \(-a\) in \(x\)-Richtung.
Verschiebung um \(\boldsymbol{-a}\) in \(\boldsymbol{x}\)-Richtung
\[g(x) = f(x + a)\]
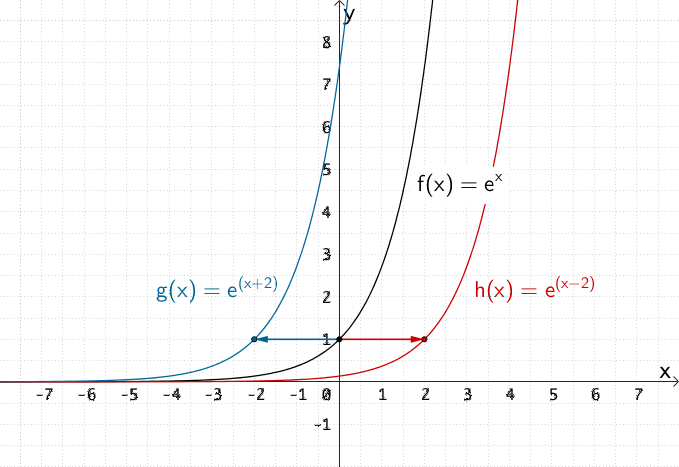
Der Graph der Funktion \(g\) entsteht durch Verschiebung des Graphen der Funktion \(f\) um \(-2\) in \(x\)-Richtung.
Der Graph der Funktion \(h\) entsteht durch Verschiebung des Graphen der Funktion \(f\) um \(+2\) in \(x\)-Richtung.
Strecken/Stauchen von Funktionsgraphen
Streckung/Stauchung in \(y\)-Richtung
Der Graph der Funktion \(g\) mit \(g(x) = k \cdot f(x)\) entsteht durch Streckung bzw. Stauchung des Graphen der Funktion \(f\) um den Faktor \(k\) in \(y\)-Richtung. Dabei bewirkt \(k > 0\) eine Streckung und \(0 < k < 1\) eine Stauchung in \(y\)-Richtung.
Streckung/Stauchung um \(\boldsymbol{k}\) in \(\boldsymbol{y}\)-Richtung
\[g(x) = k \cdot f(x)\]
\(k > 0\): Streckung
\(0 < k < 1\): Stauchung
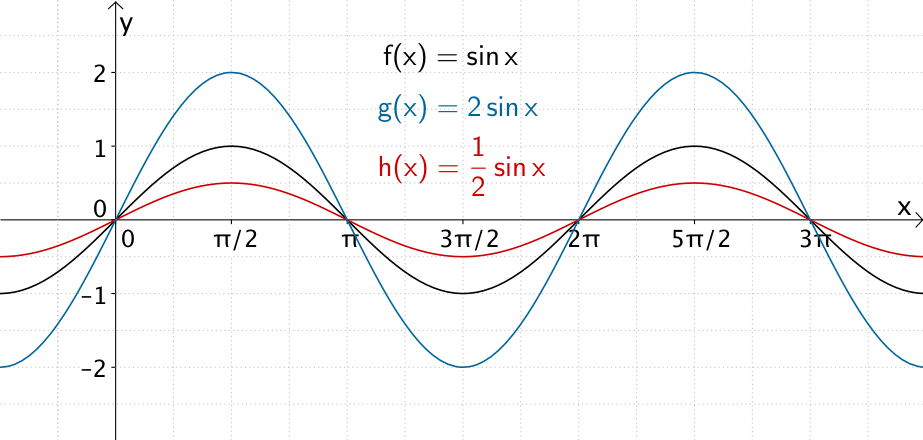
Der Graph der Funktion \(g\) entsteht durch Streckung des Graphen der Funktion \(f\) um den Faktor \(2\) in \(y\)-Richtung.
Der Graph der Funktion \(h\) entsteht durch Streckung des Graphen der Funktion \(f\) um den Faktor \(\frac{1}{2}\) in \(y\)-Richtung (entspricht einer Stauchung um den Faktor \(2\)).
Streckung/Stauchung in \(x\)-Richtung
Der Graph der Funktion \(g\) mit \(g(x) = f(k \cdot x)\) entsteht durch Streckung bzw. Stauchung des Graphen der Funktion \(f\) um den Faktor \(\frac{1}{k}\) in \(x\)-Richtung. Dabei bewirkt \(k > 0\) eine Stauchung und \(0 < k < 1\) eine Streckung in \(x\)-Richtung.
Streckung/Stauchung um \(\boldsymbol{\frac{1}{k}}\) in \(\boldsymbol{x}\)-Richtung
\[g(x) = f(k \cdot x)\]
\(k > 0\): Stauchung
\(0 < k < 1\): Streckung
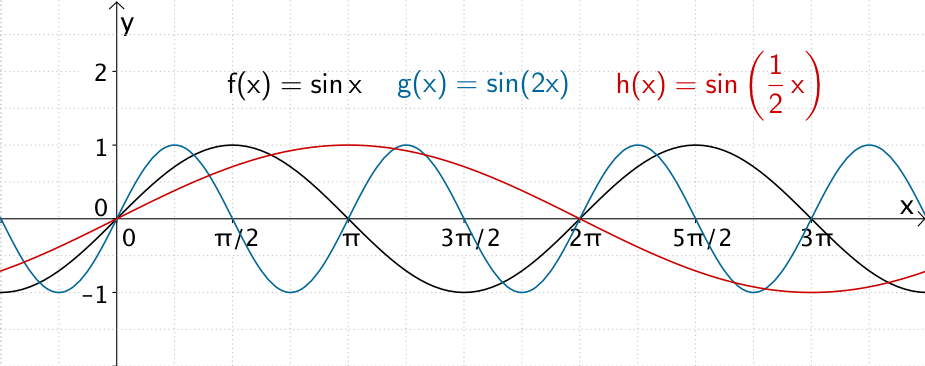
Der Graph der Funktion \(g\) entsteht durch Streckung des Graphen der Funktion \(f\) um den Faktor \(\frac{1}{2}\) in \(x\)-Richtung (entspricht einer Stauchung um den Faktor \(2\)).
Der Graph der Funktion \(h\) entsteht durch Streckung des Graphen der Funktion \(f\) um den Faktor \(2\) in \(x\)-Richtung.
Spiegeln von Funktionsgraphen an den Koordinatenachsen
Spiegelung an der \(x\)-Achse
Der Graph der Funktion \(g\) mit \(g(x) = -f(x)\) entsteht durch Spiegelung des Graphen der Funktion \(f\) an der \(x\)-Achse.
Spiegelung an der \(\boldsymbol{x}\)-Achse
\[g(x) = -f(x)\]
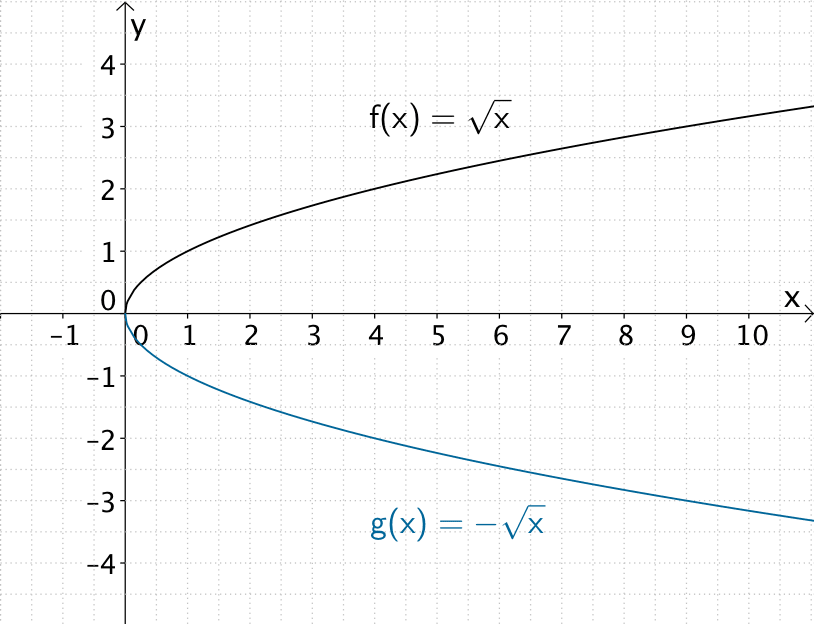
Der Graph der Funktion \(g\) entsteht durch Spiegelung des Graphen der Funktion \(f\) an der \(x\)-Achse.
Spiegelung an der \(y\)-Achse
Der Graph der Funktion \(g\) mit \(g(x) = f(-x)\) entsteht durch Spiegelung des Graphen der Funktion \(f\) an der \(y\)-Achse.
Spiegelung an der \(\boldsymbol{y}\)-Achse
\[g(x) = f(-x)\]
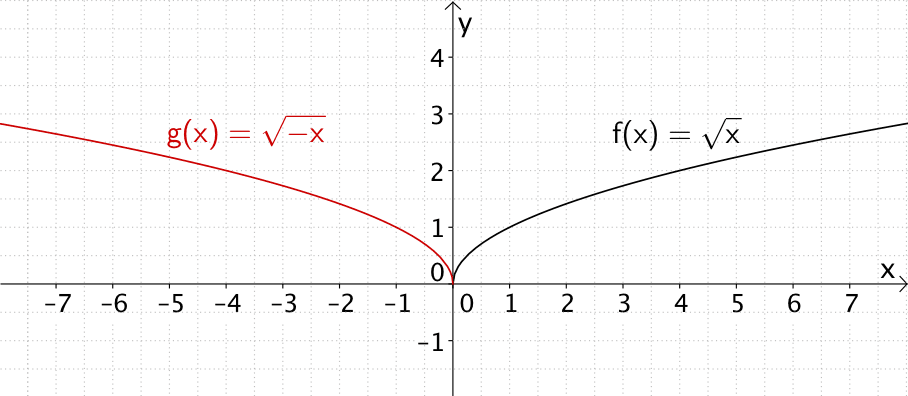
Der Graph der Funktion \(g\) entsteht durch Spiegelung des Graphen der Funktion \(f\) an der \(y\)-Achse.
Beispielaufgabe
Beschreiben Sie schrittweise, wie der Graph der Funktion \(h\colon x \mapsto 0{,}5e^{\frac{x}{2}- 1} - 3\) aus dem Graphen der Funktion \(f\colon x \mapsto e^{x}\) entsteht.
\[f(x) = e^{x}\,; \quad h(x) = 0{,}5e^{\frac{x}{2}- 1} - 3\]
1. Streckung in \(y\)-Richtung um den Faktor \(0{,}5\) (entspricht einer Stauchung um den Faktor \(2\))
\[\Longrightarrow \quad f_{1}(x) = 0{,}5f(x) = 0{,}5e^{x}\]
2. Streckung in \(x\)-Richtung um den Faktor \(2\)
\[\Longrightarrow \quad f_{2}(x) = f_{1}(\textstyle{\frac{1}{2}}x) = 0{,}5e^{\frac{x}{2}} \]
3. Verschiebung um \(-3\) in \(y\)-Richtung
\[\Longrightarrow \quad f_{3}(x) = f_{2}(x) - 3 = 0{,}5e^{\frac{x}{2}} - 3\]
4. Verschiebung um \(2\) in \(x\)-Richtung
\[\Longrightarrow \quad f_{4}(x) = f_{3}(x - 2) = 0{,}5e^{\frac{x - 2}{2}} - 3 = 0{,}5e^{\frac{x}{2} - 1} - 3 = h(x)\]
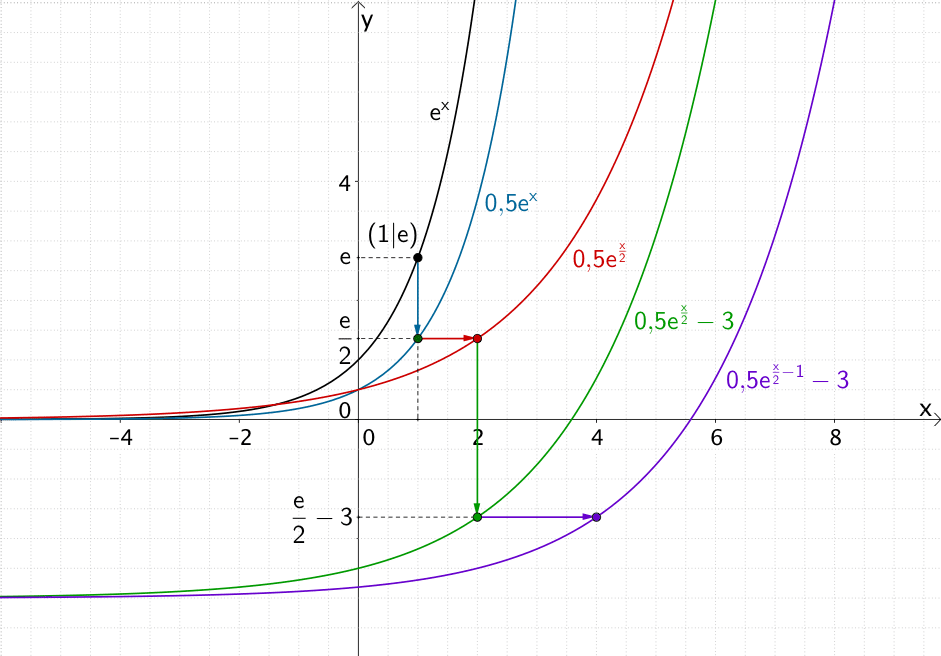
Entstehung des Graphen der Funktion \(h\colon x \mapsto 0{,}5e^{\frac{x}{2}- 1} - 3\) aus dem Graphen der Funktion \(f\colon x \mapsto e^{x}\)


