Geben Sie jeweils den Term und den Definitionsbereich einer Funktion an, die die angegebene(n) Eigenschaft(en) besitzt.

Der Punkt \((2|0)\) ist ein Wendepunkt des Graphen von \(g\).

(2 BE)

Lösung zu Teilaufgabe 2a

Entwicklung von Funktionen

1. Lösungsansatz: Sinusfunktion 

Die Nullstellen \(x = k \cdot \pi\) mit \(k \in \mathbb Z\) der Sinusfunktion \(f \colon x \mapsto \sin x\) mit \(D = \mathbb R\) sind zugleich Wendestellen. Für \(k = 0\) ist \(x = 0\) eine dieser Wendestellen. Verschiebt man den Graphen der Sinusfunktion \(f\) um 2 in positive \(x\)-Richtung, so besitzt der Graph der entstehenden und ebenfalls in \(\mathbb R\) definierten Funktion \(g\) den Wendepunkt \(W(2|0)\).

\[f(x) = \sin{x}; \; D = \mathbb R\]

\[g(x) = f(x - 2) = \sin(x - 2)\]

\[\Longrightarrow \quad g(x) = \sin(x - 2); \; D = \mathbb R\]

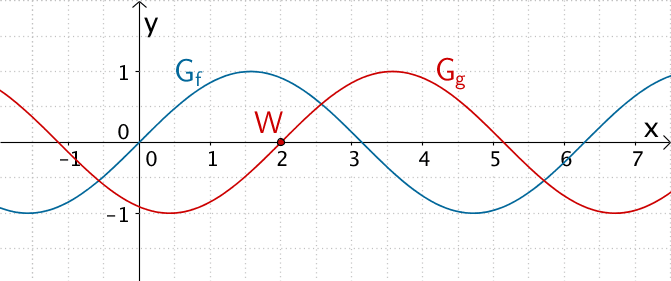
Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto \sin{x}\) und Graph der ebenfalls in \(\mathbb R\) definierten Funktion \(g \colon x \mapsto \sin(x - 2)\) mit Wendepunkt \(W(2|0)\)

Alternative:

Da die Nullstellen der Sinusfunktion \(x \mapsto \sin x\) zugleich Wendestellen sind, haben alle Sinusfunktionen der Form \(x \mapsto a \cdot \sin (b \cdot x)\) mit \(a \in \mathbb R\) und \(b \neq 0\), welche für \(x = 2\) eine Nullstelle besitzen, den Wendepunkt \((2|0)\).

Die Amplitude \(a\) wirkt sich nicht auf die Lage der Nullstellen aus. Das heißt es muss gelten:

\[\sin(b \cdot 2) = 0; \; b \neq 0\]

Die Nullstellen der Sinusfunktion \(x \mapsto \sin x\) sind \(x = k \cdot \pi\) mit \(k \in \mathbb Z\). Damit ergibt sich folgende Bedingung:

\[\begin{align*}b \cdot 2 = k \cdot \pi & &| : 2 \\[0.8em] b = k \cdot \frac{\pi}{2}; \; k \neq 0\end{align*}\]

\[\Longrightarrow \quad g_{a,k}(x) = a \cdot \sin\left(k \frac{\pi}{2} \cdot x \right); \; a \in \mathbb R, \, k \in \mathbb Z, \, k \neq 0\]

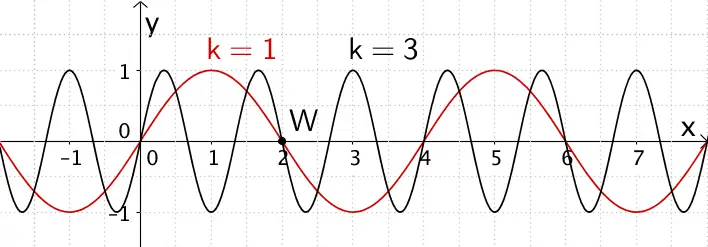
Graphen der Funktionenschar \(g_{a,k} \colon x \mapsto a \cdot \sin\left(k\dfrac{\pi}{2} \cdot x\right)\) für \(a = 1\) und \(k = 1\) bzw. \(k = 3\)

2. Lösungsansatz: Ganzrationale Funktion dritten Grades

Wählt man als Ansatz eine zum Koordinatenursprung punktsymmetrische, in \(\mathbb R\) definierte,  ganzrationale Funktion \(f\) dritten Grades, welche für \(x < 0\) und \(x > 0\) je eine einfache Nullstelle hat, so besitzt der Graph dieser Funktion einen Hochpunkt und einen Tiefpunkt sowie einen Wendepunkt im Koordinatenursprung. Verschiebt man den Graphen der ganzrationalen Funktion \(f\) um 2 in positive \(x\)-Richtung, so besitzt der Graph der entstehenden und ebenfalls in \(\mathbb R\) definierten ganzrationalen Funktion \(g\) den Wendepunkt \(W(2|0)\).

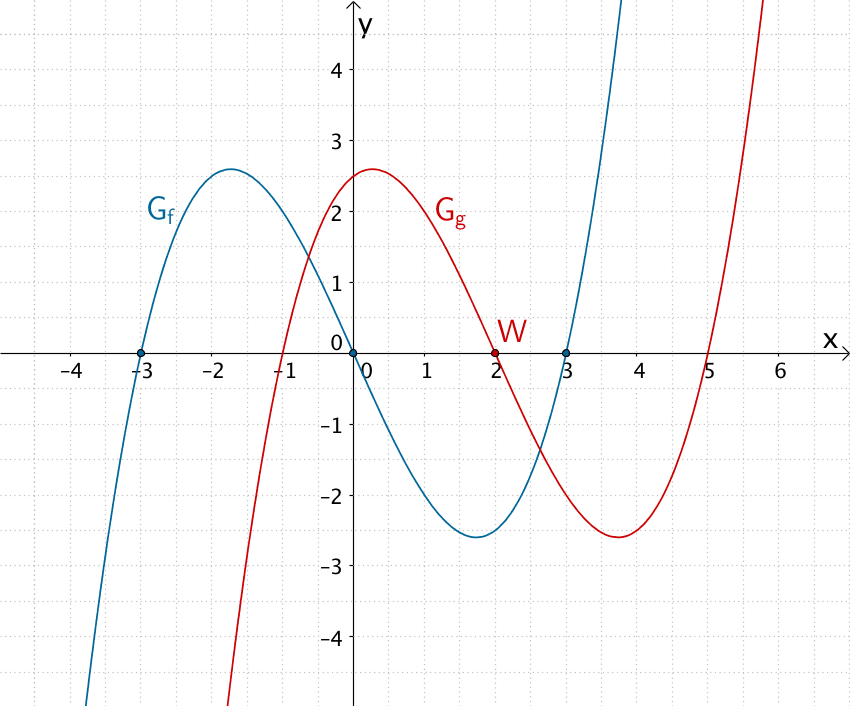
Den Funktionsterm von \(f\) gibt man anhand der Nullstellen in der vollständig faktorisierten Form an.

Beispielsweise lautet dieser (vgl. Abbildung):

\[f_{a}(x) = a \cdot x \cdot (x - 3) \cdot (x + 3); \; D_{f} = \mathbb R\]

Der Wert für den Parameter \(a\) ist in \(\mathbb R\) frei wählbar. Er streckt oder staucht den Graphen der Funktion \(f\) in \(y\)-Richtung (für a < 0 zusätzlich Spiegelung an der \(x\)-Achse), ohne die Punktsymmetrie und den Wendepunkt im Koordinatenursprung zu beeinflussen. Die Abbildung zeigt \(G_{f}\) für \(a = 0{,}25\).

\[f(x) = 0{,}25 x(x -3)(x + 3); \; D_{f} = \mathbb R\]

Abschließend verschiebt man \(G_{f}\) um 2 in positive \(x\)-Richtung um \(G_{g}\) zu erhalten und ermittelt den zugehörigen Funktionsterm \(g(x)\).

\[\begin{align*}g(x) &= f(x - 2) \\[0.8em] &= 0{,}25(x - 2)(x - 2 - 3)(x - 2 + 3) \\[0.8em] &= 0{,}25(x - 2)(x - 5)(x + 1) \end{align*}\]

\[\Longrightarrow \quad g(x) = 0{,}25(x - 2)(x - 5)(x + 1); \; D_{g} = \mathbb R\]

Allgemeine Betrachtung:

Es seien \(-c\) und \(c\) die reellen Nullstellen der in \(\mathbb R\) definierten ganzrationalen Funktionschar \(f_{a,c} \colon \mapsto a \cdot x \cdot (x - c) \cdot (x + c)\) dritten Grades mit \(a,c \in \mathbb R\).

Verschiebt man die Graphen von \(f_{a,c}\) um 2 in positive \(x\)-Richtung, so besitzen die Graphen der entstehenden und ebenfalls in \(\mathbb R\) definierten Funktionenschar \(g_{a,c}\) den Wendepunkt \((2|0)\).

Funktionsterm der Funktioenschar \(g_{a,c}\):

\[f_{a,c}(x) = a \cdot x \cdot (x - c) \cdot (x + c); \; D_{f_{a,c}} = \mathbb R, \; a,c \in \mathbb R\]

\[\begin{align*}g_{a,c}(x) &= f_{a,c}(x - 2) \\[0.8em] &= a \cdot (x - 2) \cdot (x - 2 - c) \cdot (x - 2 + c)\end{align*}\]

\[\Longrightarrow \quad g_{a,c}(x) = a \cdot (x - 2) \cdot (x - 2 - c) \cdot (x - 2 + c); \; D_{g_{a,c}} = \mathbb R, \; a,c \in \mathbb R\]