Um die Sonneneinstrahlung im Laufe des Tages möglichst effektiv zur Energiegewinnung nutzen zu können, lässt sich das Metallrohr mit dem Solarmodul um die Längsachse des Rohrs drehen. Die Größe des Neigungswinkels \(\varphi\) gegenüber der Horizontalen bleibt dabei unverändert. Betrachtet wird der Eckpunkt des Solarmoduls, der im Modell durch den Punkt \(A\) dargestellt wird. Berechnen Sie den Radius des Kreises, auf dem sich dieser Eckpunkt des Solarmoduls bei der Drehung des Metallrohrs bewegt, auf Zentimeter genau.
(4 BE)
Lösung zu Teilaufgabe f
1. Lösungsansatz: Lage der Punkte \(A\) und \(M\) betrachten
2. Lösungsansatz: Abstand Punkt - Gerade
- 1. Möglichkeit: Skalarprodukt orthogonaler (senkrechter) Vektoren anwenden
- 2. Möglichkeit: Hilfsebene aufstellen
- 3. Möglichkeit: Differentialrechnung anwenden (Extremwertaufgabe)
3. Lösungsansatz: Elementargeometrische Beziehungen im rechtwinkligen Dreieck
4. Lösungsansatz: Senkrechte Projektion der Strecke \([AM]\) auf die \(x_{1}x_{2}\)-Ebene
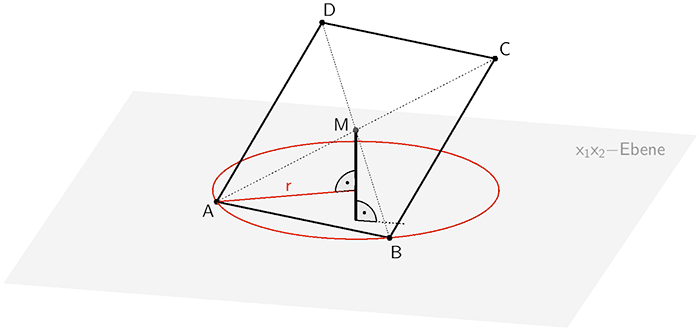
Kreis mit Radius \(r\), auf dem sich im Modell der Eckpunkt \(A\) des Solarmoduls (Viereck \(ABCD\)) bei der Drehung des Metallrohrs bewegt.
1. Lösungsansatz: Lage der Punkte \(A\) und \(M\) betrachten
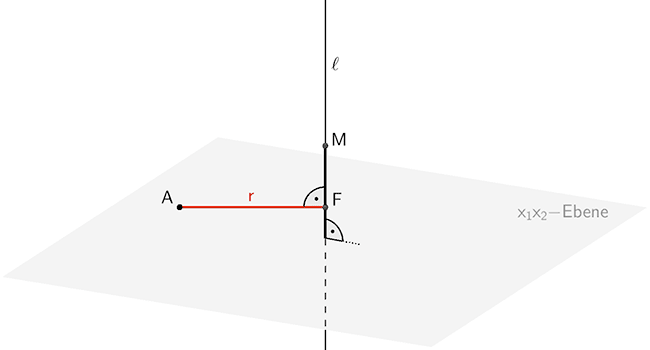
Das Metallrohr steht senkrecht auf der \(x_{1}x_{2}\)-Ebene und lässt sich um die Längsachse drehen (vgl. Angabe Teilaufgaben d,f). Die Lotgerade \(\ell\) durch den Punkt \(M\) auf die \(x_{1}x_{2}\)-Ebene beschreibt die Längsachse des Metallrohrs. Das Lot des Punktes \(A\) auf die Lotgerade \(\ell\) legt den Lotfußpunkt \(F\) fest. Dieser ist der Mittelpunkt des Kreises, auf dem sich der Punkt \(A\) bei der Drehung bewegt.
\[r = \vert \overrightarrow{AF} \vert\]
Die Punkte \(M\) und \(F\) liegen auf der Lotgeraden \(\ell\) und haben somit die gleiche \(x_{1}\)- und \(x_{2}\)- Koordinate.
\(M(-2|4|3)\) (vgl. Teilaufgabe b)
\(M, F \in \ell \quad \Longrightarrow \quad F(-2|4|x_{3})\)
Die Strecke \([AF]\) ist zur Lotgeraden \(\ell\) senkrecht und verläuft damit parallel zur \(x_{1}x_{2}\)-Ebene. Folglich haben die Punkte \(A\) und \(F\) die gleiche \(x_{3}\)-Koordinate.
\(A(0|0|1)\) (vgl. Angabe)
\[[AF] \parallel x_{1}x_{2}\text{-Ebene} \quad \Longrightarrow \quad F(-2|4|1)\]
Radius \(r\) des Kreises berechnen, auf dem sich der Eckpunkt \(A\) bewegt:
Eine Längeneinheit im Modell entspricht \(0{,}8\,\sf{m}\) in der Realität (vgl. Angabe Teilaufgabe d).
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}r &= \vert \overrightarrow{AF} \vert \cdot 0{,}8\,\sf{m} \\[0.8em] &= \vert \overrightarrow{F} - \overrightarrow{A} \vert \cdot 0{,}8\,\sf{m} \\[0.8em] &= \left| \begin{pmatrix} -2 \\ 4 \\ 1 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right| \cdot 0{,}8\,\sf{m} \\[0.8em] &= \left| \begin{pmatrix} -2 \\ 4 \\ 0 \end{pmatrix} \right| \cdot 0{,}8\,\sf{m} \\[0.8em] &= \sqrt{(-2)^{2} + 4^{2} + 0^{2}} \cdot 0{,}8\,\sf{m} \\[0.8em] &= 2\sqrt{5} \cdot 0{,}8\,\sf{m} \\[0.8em] &\approx 3{,}58\,\sf{m} \end{align*}\]
Der Eckpunkt \(A\) des Solarmoduls bewegt sich bei der Drehung des Metallrohrs auf einem Kreis mit einem Radius von ca. 3,58 m.
2. Lösungsansatz: Abstand Punkt - Gerade

Betrachtet wird der Abstand des Punktes \(A\) von der Lotgeraden \(\ell\) durch den Punkt \(M\) auf die \(x_{1}x_{2}\)-Ebene. Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(A\) auf die Lotgerade \(\ell\).
\[r = d(A;\ell) = d(A;F) = \vert \overrightarrow{AF} \vert\]
Nachfolgend werden drei Möglichkeiten vorgestellt, den Verbindungsvektor \(\overrightarrow{AF}\) und damit den Radius \(r\) zu ermitteln.
1. Möglichkeit: Skalarprodukt orthogonaler (senkrechter) Vektoren anwenden
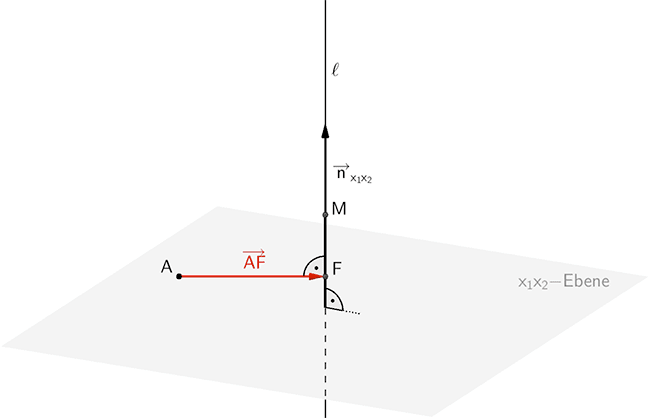
Die Lotgerade \(\ell\) ist durch den Punkt \(M\) und einen Normalenvektor \(\overrightarrow{n}_{x_{1}x_{2}}\) der \(x_{1}x_{2}\)-Ebene eindeutig festgelegt. Der Vierbindunsvektor \(\overrightarrow{AF}\) und der Normalenvektor \(\overrightarrow{n}_{x_{1}x_{2}}\) sind zueinander senkrecht. Folglich ist das Skalarprodukt der Vektoren gleich Null.
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\(M(-2|4|3)\) (vgl. Teilaufgabe b)
Beispielsweise ist \(\overrightarrow{n}_{x_{1}x_{2}} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\) ein Normalenvektor der \(x_{1}x_{2}\)-Ebene.
\[\begin{align*}\ell \colon \overrightarrow{X} &= \overrightarrow{M} + \mu \cdot \overrightarrow{n}_{x_{1}x_{2}} \\[0.8em] \ell \colon \overrightarrow{X} &= \begin{pmatrix} -2 \\ 4 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R \end{align*}\]
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{AF} \perp \overrightarrow{n}_{x_{1}x_{2}} \quad \Longleftrightarrow \quad \overrightarrow{AF} \circ \overrightarrow{n}_{x_{1}x_{2}} = 0\]
Der Verbindungsvektor \(\overrightarrow{AF}\) lässt sich mit \(F \in \ell\) in Abhängigkeit des Parameters \(\mu\) der Gleichung der Lotgeraden \(\ell\) beschreiben.
\(A(0|0|1)\) (vgl. Angabe)
\[\ell \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ 4 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R \]
\[F \in \ell \colon \overrightarrow{F} = \begin{pmatrix} -2 \\ 4 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 3 + \mu \end{pmatrix}\]
\[\overrightarrow{AF} = \overrightarrow{F} - \overrightarrow{A} = \begin{pmatrix} -2 \\ 4 \\ 3 + \mu \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 2 + \mu \end{pmatrix}\]
Skalarprodukt der orthogonalen Vektoren \(\overrightarrow{AF}\) und \(\overrightarrow{n}_{x_{1}x_{2}}\) anwenden:
Die Lösung der Gleichung liefert genau den Wert des Parameters \(\mu\), der den Verbindungsvektor \(\overrightarrow{AF}\) festlegt, sodass \(r = \vert \overrightarrow{AF} \vert\) gilt.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \overrightarrow{AF} \circ \overrightarrow{n}_{x_{1}x_{2}} &= 0 \\[0.8em] \begin{pmatrix} -2 \\ 4 \\ 2 + \mu \end{pmatrix} \circ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} &= 0 \\[0.8em] (-2) \cdot 0 + 4 \cdot 0 + (2 + \mu) \cdot 1 &= 0 \\[0.8em] 2 + \mu &= 0 & &| - 2 \\[0.8em] \mu &= -2 \end{align*}\]
Koordinaten des Verbindungektors \(\overrightarrow{AF}\) berechnen:
\[\overrightarrow{AF} = \begin{pmatrix} -2 \\ 4 \\ 2 + \mu \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 2 - 2 \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 0 \end{pmatrix}\]
Radius \(r\) des Kreises berechnen, auf dem sich der Eckpunkt \(A\) bewegt:
Eine Längeneinheit im Modell entspricht \(0{,}8\,\sf{m}\) in der Realität (vgl. Angabe Teilaufgabe d).
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}r &= \vert \overrightarrow{AF} \vert \cdot 0{,}8\,\sf{m} \\[0.8em] &= \left| \begin{pmatrix} -2 \\ 4 \\ 0 \end{pmatrix} \right| \cdot 0{,}8\,\sf{m} \\[0.8em] &= \sqrt{(-2)^{2} + 4^{2} + 0^{2}} \cdot 0{,}8\,\sf{m} \\[0.8em] &= 2\sqrt{5} \cdot 0{,}8\,\sf{m} \\[0.8em] &\approx 3{,}58\,\sf{m} \end{align*}\]
Der Eckpunkt \(A\) des Solarmoduls bewegt sich bei der Drehung des Metallrohrs auf einem Kreis mit einem Radius von ca. 3,58 m.
2. Möglichkeit: Hilfsebene aufstellen
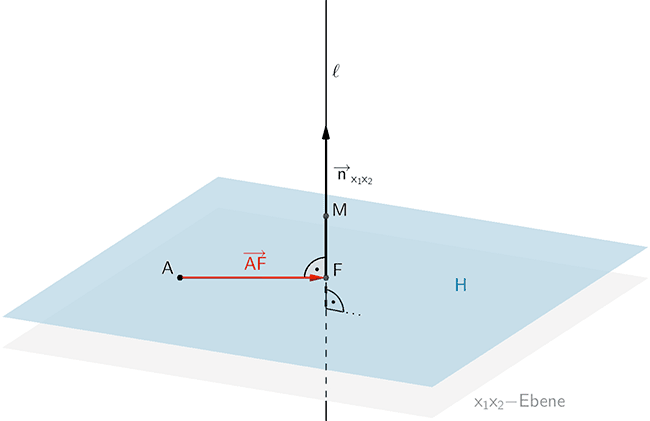
Die Hilfsebene \(H\) mit den Eigenschaften \(A \in H\) und \(H \perp \ell\) schneidet die Lotgerade \(\ell\) im Lotfußpunkt \(F\) des Lotes des Punktes \(A\) auf die Lotgerade \(\ell\).
In diesem Fall gilt \(H \parallel x_{1}x_{2}\text{-Ebene}\) und mit \(A(0|0|1) \in H\) folgt:
\[H \colon x_{3} = 1\]
Der Verbindungsvektor \(\overrightarrow{AF}\) lässt sich mit \(F \in \ell\) in Abhängigkeit des Parameters \(\mu\) der Gleichung der Lotgeraden \(\ell\) beschreiben.
\(A(0|0|1)\)
\[\ell \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ 4 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R \]
\[F \in \ell \colon \overrightarrow{F} = \begin{pmatrix} -2 \\ 4 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 3 + \mu \end{pmatrix}\]
\[\overrightarrow{AF} = \overrightarrow{F} - \overrightarrow{A} = \begin{pmatrix} -2 \\ 4 \\ 3 + \mu \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 2 + \mu \end{pmatrix}\]
Schneidet man die Lotgerade \(\ell\) mit der Hilfsebene \(H\), erhält man genau den Wert des Parameters \(\mu\), der den Verbindungsvektor \(\overrightarrow{AF}\) festlegt, sodass \(r = \vert \overrightarrow{AF} \vert\) gilt.
\[\ell \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ 4 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R \]
\[H \colon x_{3} = 1\]
\[\begin{align*} \ell \cap H \colon 3 + \mu &= 1 & &| -3 \\[0.8em] \mu &= -2 \end{align*}\]
Koordinaten des Verbindungektors \(\overrightarrow{AF}\) berechnen:
\[\overrightarrow{AF} = \begin{pmatrix} -2 \\ 4 \\ 2 + \mu \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 2 - 2 \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 0 \end{pmatrix}\]
Radius \(r\) des Kreises berechnen, auf dem sich der Eckpunkt \(A\) bewegt:
Eine Längeneinheit im Modell entspricht \(0{,}8\,\sf{m}\) in der Realität (vgl. Angabe Teilaufgabe d).
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}r &= \vert \overrightarrow{AF} \vert \cdot 0{,}8\,\sf{m} \\[0.8em] &= \left| \begin{pmatrix} -2 \\ 4 \\ 0 \end{pmatrix} \right| \cdot 0{,}8\,\sf{m} \\[0.8em] &= \sqrt{(-2)^{2} + 4^{2} + 0^{2}} \cdot 0{,}8\,\sf{m} \\[0.8em] &= 2\sqrt{5} \cdot 0{,}8\,\sf{m} \\[0.8em] &\approx 3{,}58\,\sf{m} \end{align*}\]
Der Eckpunkt \(A\) des Solarmoduls bewegt sich bei der Drehung des Metallrohrs auf einem Kreis mit einem Radius von ca. 3,58 m.
3. Möglichkeit: Differentialrechnung anwenden (Extremwertaufgabe)
![Strecke [AX] zwischen dem Punkt A und einem beliebigen Punkt X ∈ ℓ Strecke [AX] zwischen dem Punkt A und einem beliebigen Punkt X ∈ ℓ](/images/stories/B2017_PT_B_G_1/B2017_PT_B_G_1_f_4.png)
Die Länge der Strecke \([AX]\) zwischen dem Punkt \(A\) und einem beliebigen Punkt \(X \in \ell\) ist für \(X = F\) minimal.
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overline{AX} = \vert \overrightarrow{AX} \vert\]
Notwendige Bedingung für die minimale Länge der Strecke \([AX]\):
\[\overline{AX}' = 0\]
Der Verbindungsvektor \(\overrightarrow{AX}\) lässt sich mit \(X \in \ell\) in Abhängigkeit des Parameters \(\mu\) der Gleichung der Lotgeraden \(\ell\) beschreiben.
\(A(0|0|1)\)
\[\ell \colon \overrightarrow{X} = \begin{pmatrix} -2 \\ 4 \\ 3 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 3 + \mu \end{pmatrix}\]
\[\overrightarrow{AX} = \overrightarrow{X} - \overrightarrow{A} = \begin{pmatrix} -2 \\ 4 \\ 3 + \mu \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 4 \\ 2 + \mu \end{pmatrix}\]
Länge der Strecke \([AX]\) in Abhängigkeit des Parameters \(\mu\) formulieren:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{AX(\mu)} &= \vert \overrightarrow{AX(\mu)} \vert \\[0.8em] &= \left| \begin{pmatrix} -2 \\ 4 \\ 2 + \mu \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-2)^{2} + 4^{2} + (2 + \mu)^{2}} \\[0.8em] &= \sqrt{4 + 14 + 4 + 4\mu + {\mu}^{2}} \\[0.8em] &= \sqrt{{\mu}^{2} + 4\mu + 24} \end{align*}\]
Notwendige Bedingung \(\overline{AX{\mu}}' = 0\) für die minimale Länge der Strecke \([AX]\) anwenden:
Der Term \(\sqrt{{\mu}^{2} + 4\mu + 24}\) kann mithilfe der Ableitung einer Wurzelfunktion bzw. der Ableitung einer Potenzfunktion, der Kettenregel sowie der Summen- und der Faktorregel abgeleitet werden.
Ableitung einer Wurzelfunktion
\[f(x) = \sqrt{g(x)} \quad \Longrightarrow \quad f'(x) = \frac{g'(x)}{2\sqrt{g(x)}} \quad (g(x) \geq 0)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} \overline{AX(\mu)}' &= 0 \\[0.8em] \left( \sqrt{{\mu}^{2} + 4\mu + 24} \right)' &= 0 \\[0.8em] \frac{2\mu + 4}{2 \cdot \sqrt{{\mu}^{2} + 4\mu + 24}} &= 0 \end{align*}\]
\[\begin{align*}\Longrightarrow \quad 2\mu + 4 &= 0 & &| - 4 \\[0.8em] 2\mu &= -4 & &| : 2 \\[0.8em] \mu &= -2 \end{align*}\]
Da der Wert eines Wurzelausdrucks minimal ist, wenn der Wert des Radikanden (Ausdruck unter der Wurzel) minimal ist, ist es ebenso möglich, die Nullstellen der ersten Ableitung des Radikanden zu betrachten.
\[\begin{align*} \overline{AX(\mu)}' &= 0 \\[0.8em] \left( \sqrt{{\mu}^{2} + 4\mu + 24} \right)' &= 0 \end{align*}\]
\[\begin{align*}\Longrightarrow \quad \left( {\mu}^{2} + 4\mu + 24 \right)' &= 0 \\[0.8em] 2\mu + 4 &= 0 & &| -4 \\[0.8em] 2\mu &= -4 & &| : 2 \\[0.8em] \mu &= -2 \end{align*}\]
Der Nachweis der Art des Extremwerts kann entfallen, denn für \(X \neq F\) nimmt die Länge der Strecke \([AX]\) einen beliebig großen Wert an. Randextrema kann es mit \(\mu \in \mathbb R\) keine geben. Somit existiert keine maximale Länge der Strecke \([AX]\).
Die Länge der Strecke \([AX(\mu)]\) ist für \(\mu = -2\) minimal und es gilt:
\[\overline{AX(-2)} = \overline{AF}\]
Minimale Länge \(\overline{AF}\) berechnen:
\[\overline{AX(\mu)} = \sqrt{{\mu}^{2} + 4\mu + 24}\]
\[\begin{align*} \overline{AF} &= \overline{AX(-2)} \\[0.8em] &= \sqrt{(-2)^{2} + 4 \cdot (-2) + 24} \\[0.8em] &= \sqrt{20} \\[0.8em] &= 2\sqrt{5} \end{align*}\]
Radius \(r\) des Kreises berechnen, auf dem sich der Eckpunkt \(A\) bewegt:
Eine Längeneinheit im Modell entspricht \(0{,}8\,\sf{m}\) in der Realität (vgl. Angabe Teilaufgabe d).
\[r = \overline{AF} \cdot \cdot 0{,}8\,\sf{m} = 2\sqrt{5} \cdot 0{,}8\,\sf{m} \approx 3{,}58\,\sf{m}\]
Der Eckpunkt \(A\) des Solarmoduls bewegt sich bei der Drehung des Metallrohrs auf einem Kreis mit einem Radius von ca. 3,58 m.
3. Lösungsansatz: Elementargeometrische Beziehungen im rechtwinkligen Dreieck
![Rechtwinkliges Dreieck AFM und rechtwinkliges Dreieck, welches der Mittelpunkt der Strecke [AB] und die Punkte F und M bilden. Rechtwinkliges Dreieck AFM und rechtwinkliges Dreieck, welches der Mittelpunkt der Strecke [AB] und die Punkte F und M bilden.](/images/stories/B2017_PT_B_G_1/B2017_PT_B_G_1_f_5.png)
Dieser elementargeometrische Lösungsansatz wendet im rechtwinkligen Dreieck \(AFM\) den Satz des Pythagoras an, wobei die Länge der Strecke \([FM]\) mithilfe einer trigonometrischen Beziehung im rechtwinkligen Dreieck \(M_{[AB]}FM\) ermittelt wird. Der Punkt \(M_{[AB]}\) ist der Mittelpunkt der Strecke \([AB]\).
Satz des Pythagoras im Dreieck \(AFM\) anwenden:
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
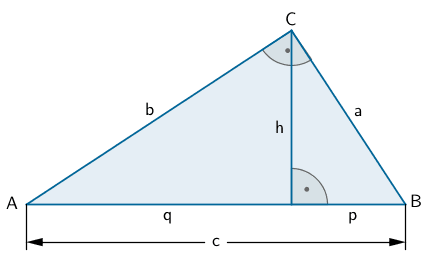
\[\begin{align*} \overline{AF}^{2} + \overline{FM}^{2} &= \overline{AM}^{2} & &| - \overline{FM}^{2} \\[0.8em] \overline{AF}^{2} &= \overline{AM}^{2} - \overline{FM}^{2} & & | \;\sqrt{\quad} \\[0.8em] &= \sqrt{\overline{AM}^{2} - \overline{FM}^{2}} \end{align*}\]
Trigonometrische Beziehung im rechtwinkligen Dreieck \(M_{[AB]}FM\) anwenden:
Aus Teilaufgabe d ist der Neigungswinkel \(\varphi\) des Solarmoduls gegenüber der Horizontalen (\(x_{1}x_{2}\)-Ebene) bekannt.
Trigonometrische Beziehungen im rechtwinkligen Dreieck
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
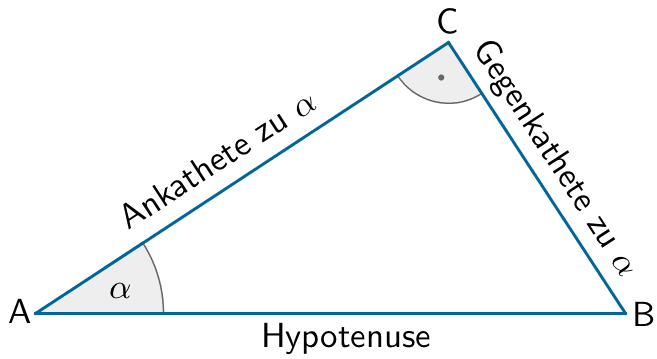
\[\begin{align*} \sin{\varphi} &= \frac{\overline{FM}}{\overline{M_{[AB]}M}} \\[0.8em] \Longleftrightarrow \enspace \overline{FM} &= \sin{\varphi} \cdot \overline{M_{[AB]}M} & &| \; \overline{M_{[AB]}M} = \frac{1}{2} \cdot \overline{AD} \\[0.8em] &= \sin{\varphi} \cdot \frac{1}{2} \cdot \overline{AD} \end{align*}\]
Längen der Strecken \([AM]\) und \([AD]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\(A(0|0|1)\), \(M(-2|4|3)\), \(D(-6|2|5)\)
\[\begin{align*} \overline{AM} &= \vert \overrightarrow{AM} \vert \\[0.8em] &= \vert \overrightarrow{M} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} -2 \\ 4 \\ 3 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -2 \\ 4 \\ 2 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-2)^{2} + 4^{2} + 2^{2}} \\[0.8em] &= \sqrt{24} \\[0.8em] &= 2\sqrt{6}\end{align*}\]
\[\begin{align*} \overline{AD} &= \vert \overrightarrow{AD} \vert \\[0.8em] &= \vert \overrightarrow{D} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} -6 \\ 2 \\ 5 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -6 \\ 2 \\ 4 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-6)^{2} + 2^{2} + 4^{2}} \\[0.8em] &= \sqrt{56} \\[0.8em] &= 2\sqrt{14}\end{align*}\]
Länge der Strecke \([FM]\) berechnen:
\(\varphi \approx 32{,}31^{\circ}\)
\[\begin{align*} \overline{FM} &= \sin{\varphi} \cdot \frac{1}{2} \cdot \overline{AD} \\[0.8em] &= \sin{32,31^{\circ}} \cdot \frac{1}{2} \cdot 2\sqrt{14} \\[0.8em] &\approx 2{,}0 \end{align*}\]
Länge der Strecke \([AF]\) berechnen:
\(\overline{AM} = \sqrt{24}\); \(\overline{FM} = 2{,}0\)
\[\overline{AF} = \sqrt{\overline{AM}^{2} - \overline{FM}^{2}} = \sqrt{\sqrt{24}^{2} - 2{,}0^{2}} = \sqrt{20} = 2\sqrt{5}\]
Radius \(r\) des Kreises berechnen, auf dem sich der Eckpunkt \(A\) bewegt:
Eine Längeneinheit im Modell entspricht \(0{,}8\,\sf{m}\) in der Realität (vgl. Angabe Teilaufgabe d).
\[r = \overline{AF} \cdot 0{,}8\,\sf{m} = 2\sqrt{5} \cdot 0{,}8\,\sf{m} \approx 3{,}58\,\sf{m}\]
Der Eckpunkt \(A\) des Solarmoduls bewegt sich bei der Drehung des Metallrohrs auf einem Kreis mit einem Radius von ca. 3,58 m.
4. Lösungsansatz: Senkrechte Projektion der Strecke \([AM]\) auf die \(x_{1}x_{2}\)-Ebene
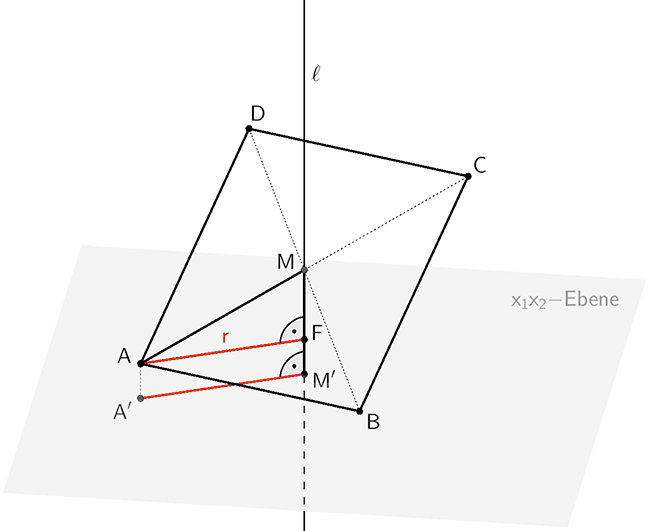
Senkrechte Projektion der Strecke \([AM]\) auf die \(x_{1}x_{2}\)-Ebene
Die Strecke \([AF]\) ist senkrecht zur Lotgeraden \(\ell\) (Längsachse des Metallrohrs) und verläuft damit parallel zur \(x_{1}x_{2}\)-Ebene.
Die Bildpunkte \(A'\) und \(M'\) gehen durch senkrechte Projektion der Punkte \(A\) und \(M\) auf die \(x_{1}x_{2}\)-Ebene hervor. Sie liegen also in der \(x_{1}x_{2}\)-Ebene.
Folglich sind die Strecken \([AF]\) und \([A'M']\) zueinander parallel und es gilt:
\[r = \overline{AF} = \overline{A'M'}\]
Koordinaten der Bildpunkte \(A'\) und \(M'\) bestimmen:
Die \(x_{3}\)-Koordinate der Bildpunkte \(A'\) und \(M'\), welche durch senkrechte Projektion der Punkte \(A\) und \(M\) auf die \(x_{1}x_{2}\)-Ebene hervorgehen, ist gleich Null.
\[A(0|0|1) \enspace \longrightarrow \enspace A'(0|0|0)\]
\[M(-2|4|3) \enspace \longrightarrow \enspace M'(-2|4|0)\]
Länge der Strecke \([A'M']\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{A'M'} &= \vert \overrightarrow{A'M'} \vert \\[0.8em] &= \vert \overrightarrow{M'} - \overrightarrow{A'} \vert & &| \; \overrightarrow{A'} = \overrightarrow{0} \\[0.8em] &= \vert \overrightarrow{M'} \vert \\[0.8em] &= \left| \begin{pmatrix} -2 \\ 4 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-2)^{2} + 4^{2} + 0^{2}} \\[0.8em] &= \sqrt{20} \\[0.8em] &= 2\sqrt{5}\end{align*}\]
Radius \(r\) des Kreises berechnen, auf dem sich der Eckpunkt \(A\) bewegt:
Eine Längeneinheit im Modell entspricht \(0{,}8\,\sf{m}\) in der Realität (vgl. Angabe Teilaufgabe d).
\[r = \overline{A'M'} \cdot 0{,}8\,\sf{m} = 2\sqrt{5} \cdot 0{,}8\,\sf{m} \approx 3{,}58\,\sf{m}\]
Der Eckpunkt \(A\) des Solarmoduls bewegt sich bei der Drehung des Metallrohrs auf einem Kreis mit einem Radius von ca. 3,58 m.


