Beschreiben Sie das Ereignis \(\overline{R} \cup \overline{V}\) im Sachzusammenhang und bestimmen Sie die Wahrscheinlichkeit dieses Ereignisses.
(4 BE)
Lösung zu Teilaufgabe 1b
Veranschaulichung des Ereignisses \(\overline{R} \cup \overline{V}\) mit Venn-Diagramm
Gesetze von de Morgan
Weder Ereignis \(A\) noch Ereignis \(B\); Keines der beiden Ereignisse
\[\overline{A} \cap \overline{B} = \overline{A \cup B}\]
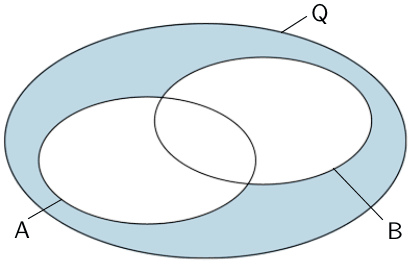
Nicht beide Ereignisse \(A\) und \(B\) zugleich; Höchstens eines der beiden Ereignisse
\[\overline{A \cap B} = \overline{A} \cup \overline{B}\]
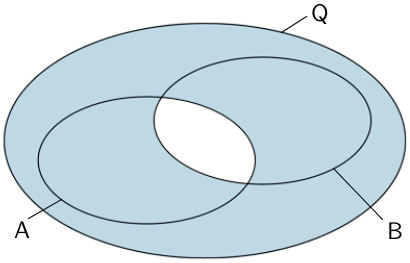
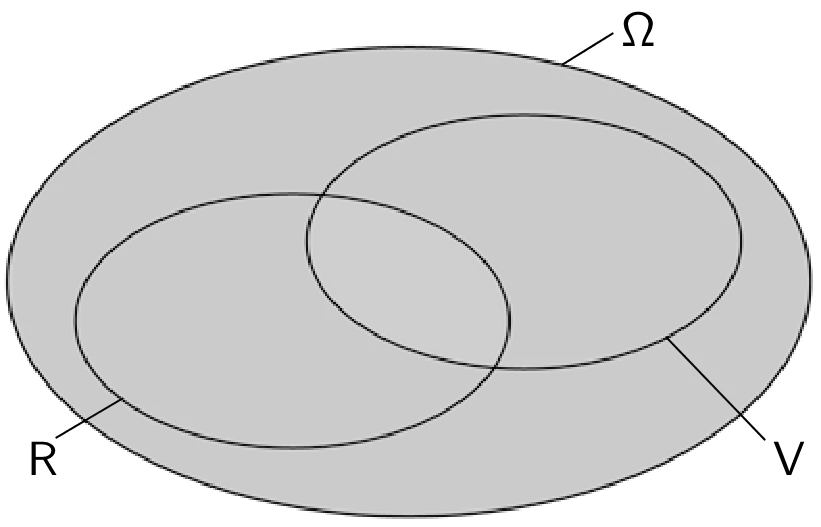
Venn-Diagramm (Mengendiagramm) für das Ereignis \(\,\overline{R} \cup \overline{V} = \overline{R \cap V}\)
Wortlaut: "Nicht beide Ereignisse \(R\) und \(V\) gleichzeitig" oder "Höchstens eines der beiden Ereignisse \(R\) und \(V\) tritt ein".
Ereignis \(\overline{R} \cup \overline{V}\) im Sachzusammenhang
"Eine aus den Befragten zufällig ausgewälte Person hat laut Umfrage zum Zeitpunkt des Kinostarts den Roman nicht gelesen oder sie hat die Verfilmung nicht gesehen."
Das mathematische "oder" der Vereinigungsmenge \(\overline{R} \cup \overline{V}\) bedeutet:
- entweder den Roman nicht gelesen oder
- die Verfilmung nicht gesehen oder
- den Roman nicht gelesen und auch die Verfilmung nicht gesehen
Eine Beschreibung des Ereignises \(\overline{R} \cup \overline{V} = \overline{R \cap V}\) im Sachzusammenhang könnte auch wie folgt lauten:
"Eine aus den Befragten zufällig ausgewälte Person hat laut Umfrage zum Zeitpunkt des Kinostarts nicht den Roman gelesen und auch die Verfilmung gesehen."
"Eine aus den Befragten zufällig ausgewälte Person hat laut Umfrage zum Zeitpunkt des Kinostarts höchstens entweder den Roman gelesen oder die Verfilmung gesehen."
Wahrscheinlichkeit des Ereignisses \(\overline{R} \cup \overline{V}\)
| \(V\) | \(\overline V\) | ||
| \(R\) | \(P(R \cap V) = 0{,}072\) | \(P(R \cap \overline{V}) = 0{,}048\) | \(P(R) = 0{,}12\) |
| \(\overline{R}\) | \(P(\overline{R} \cap V) = 0{,}108\) | \(P(\overline{R} \cap \overline{V}) = 0{,}772\) | \(P(\overline{R}) = 0{,}88\) |
| \(P(V) = 0{,}18\) | \(P(\overline{V}) = 0{,}82\) | \(1\) |
Die grau unterlegten Felder beschreiben zusammen die Wahrscheinlichkeit des Ereignisses \(\overline{R} \cup \overline{V}\).
1. Lösungsansatz: Gesetz von de Morgan / Gegenereignis
Gesetze von de Morgan
Weder Ereignis \(A\) noch Ereignis \(B\); Keines der beiden Ereignisse
\[\overline{A} \cap \overline{B} = \overline{A \cup B}\]

Nicht beide Ereignisse \(A\) und \(B\) zugleich; Höchstens eines der beiden Ereignisse
\[\overline{A \cap B} = \overline{A} \cup \overline{B}\]

\[\begin{align*}P(\overline{R} \cup \overline{V}) &= P(\overline{R \cap V}) \\[0.8em] &= 1 - P(R \cap V) \\[0.8em] &= 1 - 0{,}072 \\[0.8em] &= 0{,}928 = 92{,}8\,\%\end{align*}\]
2. Lösungsansatz: Addition der Wahrscheinlichkeiten, die \(P(\overline{R} \cup \overline{V})\) bilden
\[\begin{align*} P(\overline{R} \cup \overline{V}) &= P(\overline{R} \cap V) + P(R \cap \overline{V}) + P(\overline{R} \cap \overline{V}) \\[0.8em] &= 0{,}108 + 0{,}048 + 0{,}772 \\[0.8em] &= 0{,}928 = 92{,}8\,\%\end{align*}\]
3. Lösungsansatz: Additionssatz anwenden
Additionssatz
Für zwei beliebige Ereignisse \(A\) und \(B\) gilt:
\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]
\[\begin{align*} P(\overline{R} \cup \overline{V}) &= P(\overline{R}) + P(\overline{V}) - P(\overline{R} \cap \overline{V}) \\[0.8em] &= 0{,}88 + 0{,}82 - 0{,}772 \\[0.8em] &= 0{,}928 = 92{,}8\,\% \end{align*}\]

