Über ein Kletternetz kann man von einer Plattform zur anderen gelangen. Die vier Eckpunkte des Netzes sind an den beiden Pfählen befestigt. Einer der beiden unteren Eckpunkte befindet sich an Pfahl 1 auf der Höhe der zugehörigen Plattform, der andere untere Eckpunkt an Pfahl 2 oberhalb der Plattform 2. An jedem Pfahl beträgt der Abstand der beiden dort befestigten Eckpunkte des Netzes 1,80 m. das Netz ist so gespannt, dass davon ausgegangen werden kann, dass es die Form eines ebenen Vierecks hat.
Berechnen Sie den Flächeninhalt des Netzes und erläutern Sie Ihren Ansatz.
(3 BE)
Lösung zu Teilaufgabe e
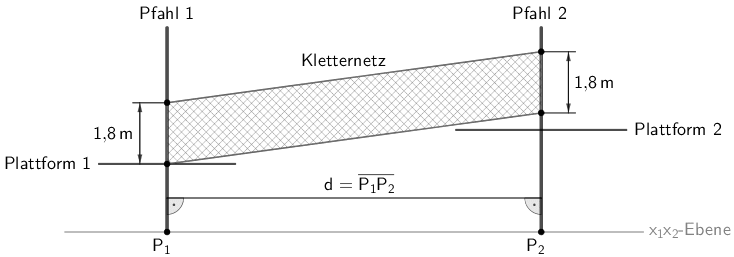
Das Kletternetz hat die Form eines Parallelogramms mit einer Grundseite \(g\) der Länge \(1{,}8\,\sf{m}\). Die Höhe \(h\) des Parallelogramms entspricht dem Abstand \(d = \overline{P_{1}P_{2}}\) der beiden Pfähle.
Abstand \(d\) der beiden Pfähle berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\(P_{1}(0|0|0)\), \(P_{2}(5|10|0)\)
\[\begin{align*}d &= \overline{P_{1}P_{2}} = \vert \overrightarrow{P_{1}P_{2}} \vert = \vert \overrightarrow{P_{2}} - \overrightarrow{P_{1}} \vert \\[0.8em] &= \left| \begin{pmatrix} 5 \\ 10 \\ 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \right| = \left| \begin{pmatrix} 5 \\ 10 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{5^{2} + 10^{2} + 0^{2}} = 5\sqrt{5} \end{align*}\]
Flächeninhalt \(A\) des Parallelogramms berechnen:
Flächeninhalt eines Parallelogramms
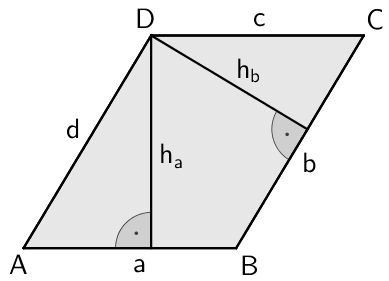
\[A = a \cdot h_a\]
bzw.
\[A = b \cdot h_{b}\]
\[A = g \cdot h = 1{,}8 \cdot \overline{P_{1}P_{2}} = 1{,}8 \cdot 5\sqrt{5} \approx 20{,}1\]
Der Flächeninhalt des Kletternetzes beträgt ca. 20,1 m².


