Betrachtet wird die Schar der in \(\mathbb R\) definierten Funktionen \(f_a\) mit \(f_a(x) = x \cdot e^{ax}\) und \(a \in \mathbb R \backslash\{0\}\). Für jeden Wert von \(a\) besitzt die Funktion \(f_a\) genau eine Extremstelle.
Begründen Sie, dass der Graph von \(f_a\) für \(x<0\) unterhalb der \(x\)-Achse verläuft.
(2 BE)
Lösung zu Teilaufgabe 3a
\[f_a(x) = x \cdot e^{ax}; \; D_f = \mathbb R, \; a \in \mathbb R \backslash \{0\}\]
Mit \(e^{ax} > 0\) gilt \(f_a(x) = x \cdot e^{ax}< 0\) für \(x < 0\). Folglich verläuft der Graph von \(f_a\) für \(x<0\) unterhalb der \(x\)-Achse.
Ausführliche Erklärung (nicht verlangt)
Die natürliche Exponentialfunktion \(x \mapsto e^x\) besitzt den Wertebereich \(\mathbb R^+\). Ihr Graph verläuft vollständig oberhalb der \(x\)-Achse.
Der Parameter \(a\) bewirkt, dass der Graph von \(x \mapsto e^{ax}\) gegenüber dem Graphen von \(x \mapsto e^x\) um den Faktor \(\dfrac{1}{a}\) in \(x\)-Richtung gestreckt ist und für \(a < 0\) zugleich an der \(y\)-Achse gespiegelt ist. Damit besitzt die Funktion \(x \mapsto e^{ax}\) ebenfalls den Wertebereich \(\mathbb R^+\) und ihr Graph verläuft vollständig oberhalb der \(x\)-Achse.
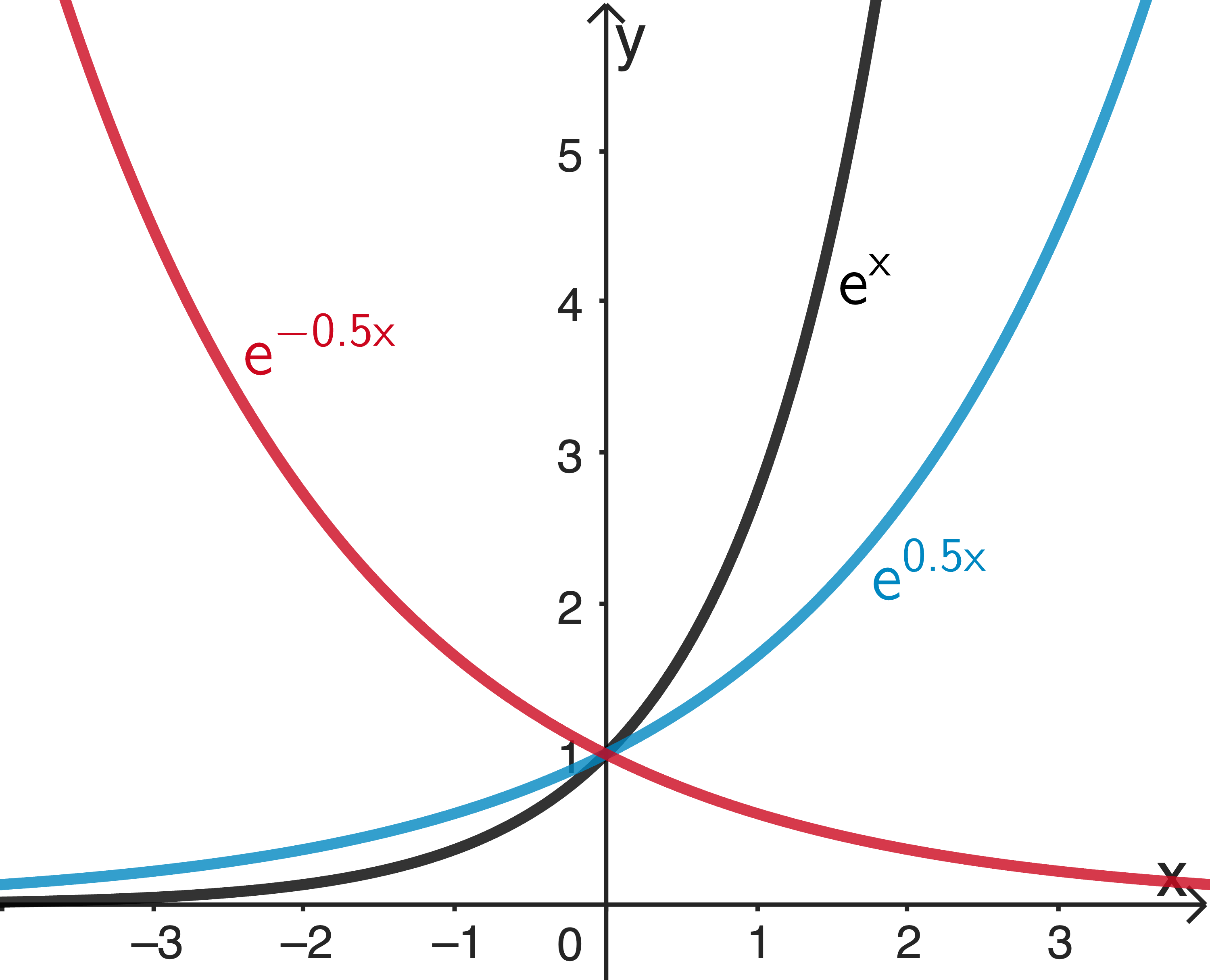
Strecken von Funktionsgraphen
Strecken mit dem Faktor \(a\) in \(y\)-Richtung
\(g(x) = a \cdot f(x)\) mit \(a \in \mathbb R^+\)
Strecken mit dem Faktor \(\dfrac{1}{b}\) in \(x\)-Richtung
\(h(x) = f(b \cdot x)\) mit \(b \in \mathbb R^+\)
Somit bestimmt das Vorzeichen des Faktors \(x\) der Funktion \(f_a \colon x \mapsto x \cdot e^{ax}\), ob der Graph von \(f_a\) oberhalb oder unterhalb der \(x\)-Achse verläuft. Für \(x > 0\) verläuft der Graph von \(f_a\) oberhalb und für \(x < 0\) unterhalb der \(x\)-Achse.


