Bestimmen Sie die Größe des Winkels, den die Seitenfläche \(BCT\) mit der Fläche \(ABCD\) einschließt.
(3 BE)
Lösung zu Teilaufgabe c
1. Möglichkeit: Trigonometrie, rechtwinkliges Dreieck

Die Größe des Winkels, den die Seitenfläche \(\textcolor{#cc071e}{BCT}\) mit der Fläche \(ABCD\) einschließt, ist gleich der Größe des Innenwinkels \(\textcolor{#0087c1}{\varphi}\), den das Stützdreieck \(\textcolor{#0087c1}{MNT}\) bei \(M\) bildet. \(M\) ist der Mittelpunkt der Seite \(\overline{BC}\) und \(N\) der Mittelpunkt (Diagonalenschnittpunkt) des Quadrats \(ABCD\).
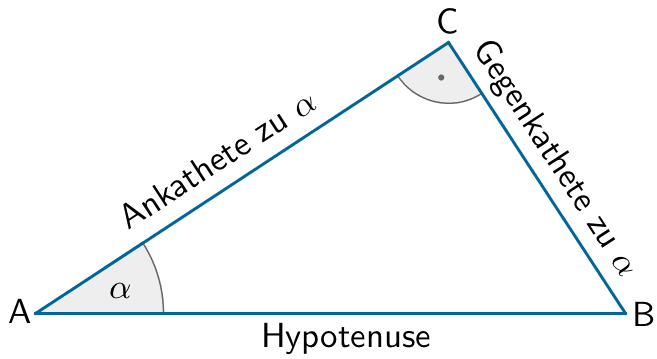
Trigonometrische Beziehungen im rechtwinkligen Dreieck
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
\[\begin{align*}\tan{\varphi} &= \frac{\textcolor{#0087c1}{\vert \overline{NT} \vert}}{\textcolor{#0087c1}{\vert \overline{MN} \vert}} = \frac{\frac{1}{2} \cdot \vert \overline{ST}\vert}{\frac{1}{2} \cdot \vert \overline{AB} \vert} = \frac{12}{5} &&| \; \text{WTR:}\; \tan^{-1}{(\dots)} \\[1.6em] \varphi &= \tan^{-1}\left( \frac{12}{5} \right) \approx 67{,}4^{\circ}\end{align*}\]
2. Möglichkeit: Schnittwinkel zweier Ebenen
Das Quadrat \(ABCD\) liegt in der Ebene \(z = 12\), die parallel zur \(xy\)-Ebene ist. Beispielsweise ist \(\overrightarrow{n}_{xy} = \begin{pmatrix} 0\\0\\1 \end{pmatrix}\) ein Normalenvektor dieser Ebene.
Die Seitenfläche \(BCT\) liegt in der Ebene \(E\). \(\overrightarrow{n}_E = \begin{pmatrix} 0\\12\\-5 \end{pmatrix}\) ist ein Normalenvektor der Ebene \(E\) (vgl. Teilaufgabe b).

Schnittwinkel \(\boldsymbol{\varphi}\) zwischen zwei Geraden


\[\begin{align*}\cos{\varphi} &= \frac{\vert \textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{v}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{v}} \vert} = \cdots \quad(0^{\circ} \leq \varphi \leq 90^{\circ}) \\[0.8em] \varphi &= \cos^{-1}(\cdots)\end{align*}\]
Der Schnittwinkel ist der spitze Winkel \((0^{\circ} < \varphi < 90^{\circ})\), den die Geraden \(\textcolor{#cc071e}{g}\) und \(\textcolor{#0087c1}{h}\) einschließen. Dieser ergibt sich für \(\cos{\varphi} \in \; ]0;1[\). Deshalb wird bei der Schnittwinkelberechnung der Betrag des Skalarprodukts \(\textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{v}}\) gewählt.
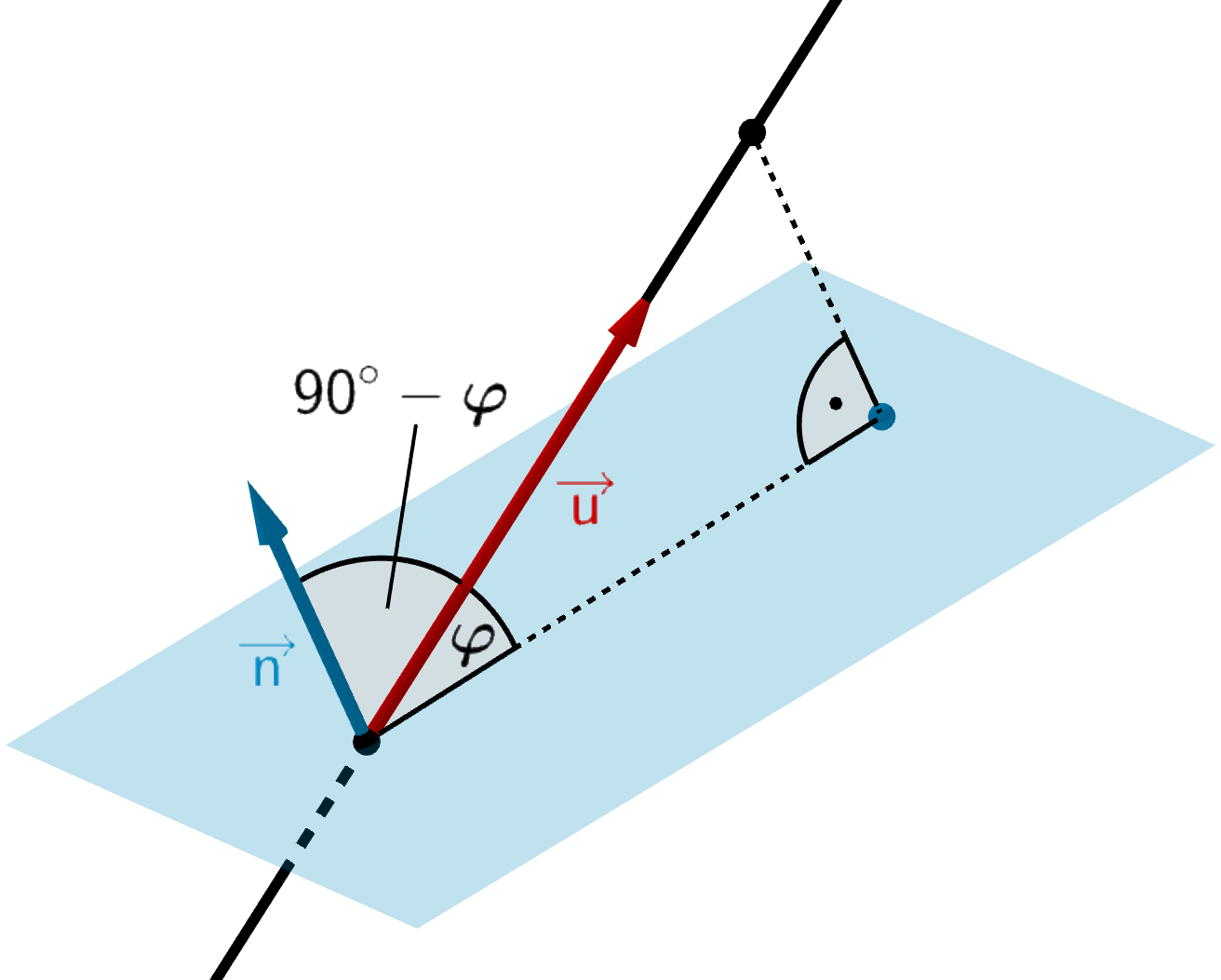
Schnittwinkel \(\boldsymbol{\varphi}\) zwischen Gerade und Ebene
\[\cos{(90^{\circ} - \varphi)} = \frac{\vert \textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{n}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}} \vert}\]
Mit \(\cos{(90^{\circ}-\varphi)} = \sin{\varphi}\) folgt:
\[\begin{align*}\sin{\varphi} &= \frac{\vert \textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{n}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}} \vert} = \cdots \quad(0^{\circ} \leq \varphi \leq 90^{\circ}) \\[0.8em] \varphi &= \sin^{-1}(\cdots)\end{align*}\]
\[\begin{align*}\cos{\varphi} &= \frac{\vert \textcolor{#0087c1}{\overrightarrow{n}_E} \circ \textcolor{#cc071e}{\overrightarrow{n}_F} \vert}{\vert \textcolor{#0087c1}{\overrightarrow{n}_E} \vert \cdot \vert \textcolor{#cc071e}{\overrightarrow{n}_F} \vert} = \cdots \quad(0^{\circ} \leq \varphi \leq 90^{\circ}) \\[0.8em] \varphi &= \cos^{-1}(\cdots)\end{align*}\]

\[\begin{align*} \cos{\varphi} &= \frac{\vert \overrightarrow{n}_{xy} \circ \overrightarrow{n}_E \vert}{\vert \overrightarrow{n}_{xy}\vert \cdot \vert \overrightarrow{n}_E \vert} = \frac{\left|\begin{pmatrix} 0\\0\\1 \end{pmatrix} \circ \begin{pmatrix} 0\\12\\-5 \end{pmatrix}\right|}{\left| \begin{pmatrix} 0\\0\\1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0\\12\\-5 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert 0 \cdot 0 + 0 \cdot 12 + 1 \cdot (-5) \vert}{1 \cdot \sqrt{0^2 + 12^2 + (-5)^2}} = \frac{5}{13} &&|\; \text{WTR:}\; \cos^{-1}{(\dots)} \\[1.6em] \varphi &= \cos^{-1}{\left( \frac{5}{13} \right)} \approx 67{,}4^{\circ} \end{align*}\]
(Vgl. Mathematik Abiturskript Bayern G9 - 3 Geometrie, 3.6 Schnittwinkelberechnungen)


