Es gibt Werte von \(m\), für die die Graphen \(G_{f}\) und \(G_{m}\) jeweils keinen gemeinsamen Punkt haben. Geben Sie diese Werte von \(m\) an.
(2 BE)
Lösung zu Teilaufgabe 3b
\[f(x) = x^{2} + 4; \; D_{f} = \mathbb R\]
\[g_{m}(x) = m \cdot x; \; D_{g_{m}} = \mathbb R; \; m \in \mathbb R\]
Für \(-4 < m < 4\) haben die Graphen \(G_{f}\) und \(G_{m}\) jeweils keinen gemeinsamen Punkt.
1. Graphische Begründung (nicht verlangt)
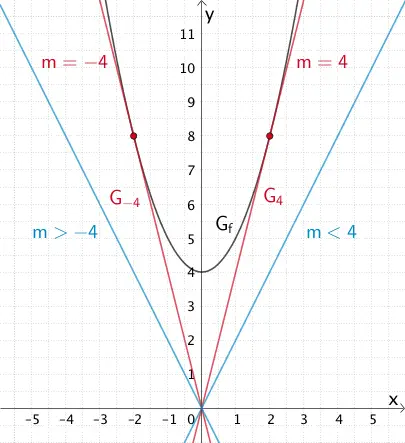
Die in \(\mathbb R\) definierte Funktion \(g_{m} \colon x \mapsto m \cdot x\) mit \(m \in \mathbb R\) beschreibt ein Büschel von Ursprungsgeraden (Geradenbüschel mit Büschelpunkt \((0|0)\)).
Für \(\textcolor{#cc071e}{m = 4}\) ist der zugehörige Graph \(\textcolor{#cc071e}{G_{4}}\) eine Tangente an \(G_{f}\) (vgl. Teilaufgabe 3a). Der zur \(y\)-Achse symmetrische Graph \(\textcolor{#cc071e}{G_{-4}}\) von \(G_{4}\) ist ebenfalls eine Tangente an \(G_{f}\). Sie hat die Steigung \(\textcolor{#cc071e}{m = -4}\).
Für \(\textcolor{#0087c1}{m > -4}\) und \(\textcolor{#0087c1}{m < 4}\) sind die zugehörigen Geraden flacher verlaufende Passanten zu \(G_{f}\).
Also haben die Graphen \(G_{f}\) und \(G_{m}\) für \(\textcolor{#0087c1}{-4 < m < 4}\) jeweils keinen gemeinsamen Punkt.
2. Rechnerische Begründung (nicht verlangt)
\[f(x) = x^{2} + 4; \; D_{f} = \mathbb R\]
\[g_{m}(x) = m \cdot x; \; D_{g_{m}} = \mathbb R; \; m \in \mathbb R\]
Durch Gleichsetzen der Funktionsterme \(f(x)\) und \(g_{m}(x)\) ergibt sich eine quadratische Gleichung, deren Anzahl der Lösungen vom Parameter \(m\) abhängt. Es sind diejenigen Werte für \(m\) zu ermitteln, sodass die quadratische Gleichung keine Lösung hat (Entspricht keine gemeinsamen Punkte von \(G_{f}\) und \(G_{m}\)).
\[\begin{align*} f(x) &= g_{m}(x) \\[0.8em] x^{2} + 4 &= m \cdot x &&| - mx \; \text{quadratische Gleichung formulieren} \\[0.8em] x^{2} - mx + 4 &= 0 &&| \; \text{Mitternachtsformel anwenden} \end{align*}\]
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[x_{1,2} = \frac{m \pm \sqrt{(-m)^{2} - 4 \cdot 1 \cdot 4}}{2 \cdot 1} = \frac{m \pm \sqrt{\textcolor{#0087c1}{m^{2} - 16}}}{2}\]
Die quadratische Gleichung hat keine Lösung, wenn für die Diskriminante \(\textcolor{#0087c1}{D = m^{2} - 16}\) git: \(D < 0\) (Der Radikand - Term unter der Wurzel - darf nicht negativ sein).
\[\begin{align*}D &< 0 \\[0.8em] m^{2} - 16 &< 0 &&| + 16 \\[0.8em] m^{2} &< 16 &&| \; \sqrt{\quad} \; \text{wobei}\; \sqrt{a^{2}} = \vert a \vert \; \text{mit}\; a \in \mathbb R \; \text{gilt}\\[0.8em] \vert m \vert &< 4 \end{align*}\]
Die Betragsungleichung lässt sich durch Fallunterscheidung lösen.
1. Fall: \(m \geq 0\)
Für \(m \geq 0\) können die Betragsstriche entfallen.
\[\Longrightarrow \quad m < 4 \]
2. Fall: \(m < 0\)
Für \(m < 0\) kann \(\vert m \vert\) durch \(-m\) ersetzt werden.
\[\begin{align*}\Longrightarrow \quad -m &< 4 &&| \cdot (-1) \enspace \textcolor{#cc071e}{\text{Relationszeichen dreht sich!}} \\[0.8em] m &\textcolor{#cc071e}{>} -4 \end{align*}\]
\[\Longrightarrow \quad - 4 < m < 4\]


