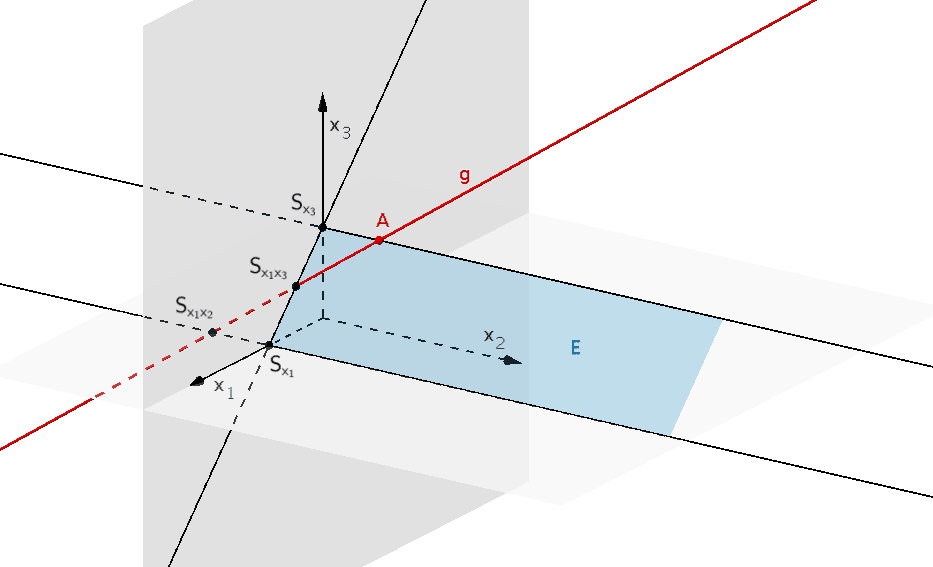
In einem kartesischen Koordinatensystem sind die Ebene \(E \colon x_{1} + x_{3} = 2\), der Punkt \(A\left( 0|\sqrt{2}|2 \right)\) und die Gerade \(\displaystyle g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\), \(\lambda \in \mathbb R\), gegeben.
Beschreiben Sie, welche besondere Lage die Ebene \(E\) im Koordinatensystem hat. Weisen Sie nach, dass die Ebene \(E\) die Gerade \(g\) enthält. Geben Sie die Koordinaten der Schnittpunkte von \(E\) mit der \(x_{1}\)-Achse und mit der \(x_{3}\)-Achse an und veranschaulichen Sie die Lage der Ebene \(E\) sowie den Verlauf der Geraden \(g\) in einem kartesischen Koordinatensystem (vgl. Abbildung).
(6 BE)
Lösung zu Teilaufgabe a
Lage einer Geraden/Ebene im Koordinatensystem, Legebeziehung Gerade/Ebene
\[E\colon x_{1} + x_{3} = 2\]
\[A\,(0|\sqrt{2}|2)\]
\[g\colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}; \enspace \lambda \in \mathbb R\]
Besondere Lage der Ebene \(E\) im Koordinatensystem
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
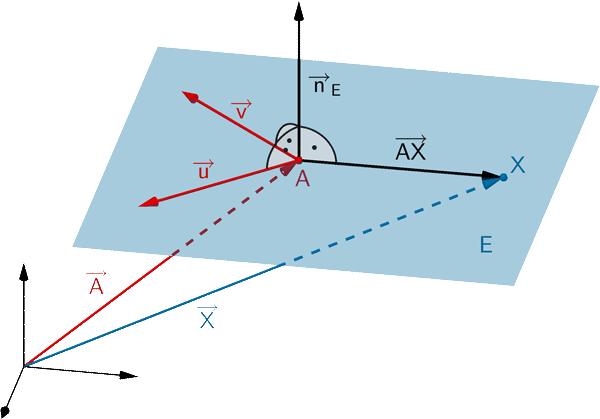
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[E\colon x_{1} + x_{3} = 2\]
Der Ebenengleichung der Ebene \(E\) entnimmt man den Normalenvektor zu \(\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}\). Da die \(x_{2}\)-Koordinate des Normalenvektors Null ist, steht der Normalenvektor senkrecht zur \(x_{2}\)-Achse. Außerdem ist ersichtlich, dass die Ebene \(E\) nicht durch den Koordinatenursprung \(O\,(0|0|0)\) verläuft, denn es gilt: \(0 + 0 \neq 2\). Folglich ist die Ebene \(E\) echt parallel zur \(x_{2}\)-Achse.
\[\left. \begin{align*} &\overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \\[0.8em] &O\,(0|0|0) \notin E \end{align*} \right\} \enspace \Rightarrow \enspace E \parallel x_{2}-Achse\]
Nachweis, dass die Ebene \(E\) die Gerade \(g\) enthält
Die Ebene \(E\) enthält die Gerade \(g\), wenn \(g \parallel E\) und \(A \in E\) gilt (da \(A \in g\)). Die Parallelität ist erfüllt, wenn der Richtungsvektor der Geraden \(g\) und der Normalenvektor der Ebene \(E\) senkrecht zueinander stehen. Zudem ist zu prüfen, ob die Koordinaten des Aufpunkts \(A\) der Geraden \(g\) die Ebenengleichung von \(E\) erfüllen.
\(g \parallel E\) nachweisen:
\[E\colon x_{1} + x_{3} = 2 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}\]
\[g\colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{n}_{E} \perp \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \quad \Longleftrightarrow \quad \overrightarrow{n}_{E} \circ \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} = 0\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \circ \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} &= 0 \\[0.8em] 1 \cdot (-1) + 0 \cdot \sqrt{2} + 1 \cdot 1 &= 0 \\[0.8em] -1 + 1 &= 0 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{E} \perp g \quad \Longrightarrow \quad g \parallel E\]
\(A \in E\) nachweisen:
\[E\colon x_{1} + x_{3} = 2\]
\[A\,(0|\sqrt{2}|2)\]
\[A \in E \colon 0 + 2 = 2 \quad \text{w}\]
\[\Longrightarrow \quad A \in E\]
Zusammenfassung:
\[\left. \begin{align*} &g \parallel E \\[0.8em] &A \in E \end{align*} \right\} \enspace \Rightarrow \enspace g \subset E\]
Die Ebene \(E\) enthält die Gerade \(g\).
Koordinaten der Schnittpunkte von \(E\) mit der \(x_{1}\)-Achse und mit der \(x_{2}\)-Achse
Die Koordinaten der Schnittpunkte \(S_{x_{1}}\) und \(S_{x_{3}}\) der Ebene \(E\) mit der \(x_{1}\)-Achse und mit der \(x_{3}\)-Achse (Spurpunkte) müssen die Ebenengleichung der Ebene \(E\) erfüllen.
\[E\colon x_{1} + x_{3} = 2\]
\[S_{x_{1}}(x_{1}|0|0) \quad \Longrightarrow \quad x_{1} + 0 = 2 \quad \Longrightarrow \quad S_{x_{1}} (2|0|0)\]
\[S_{x_{3}}(0|0|x_{3}) \quad \Longrightarrow \quad 0 + x_{3} = 2 \quad \Longrightarrow \quad S_{x_{3}} (0|0|2)\]
Als Alternative stellt man jeweils die Geradengleichung der \(x_{1}\)-Achse und der \(x_{3}\)-Achse auf und bestimmt damit die Schnittpunkte der Koordinatenachsen mit der Ebene \(E\).
\[x_{1}\text{-Achse}\, \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\]
\[E\colon x_{1} + x_{3} = 2\]
Koordinaten der Geradengleichung in die Ebenengleichung einsetzen:
\[\begin{align*}E \cap x_{1}\text{-Achse}\,\colon (0 + \lambda) + (0 + 0) &= 2 \\[0.8em] \lambda &= 2 \end{align*}\]
Parameterwert \(\lambda = 2\) in die Geradengleichung der \(x_{1}\)-Achse einsetzen:
\[\overrightarrow{S}_{x_{1}} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + 2 \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{1}} (2|0|0)\]
\[x_{3}\text{-Achse}\, \colon \overrightarrow{X} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]
\[E\colon x_{1} + x_{3} = 2\]
Koordinaten der Geradengleichung in die Ebenengleichung einsetzen:
\[\begin{align*}E \cap x_{3}\text{-Achse}\,\colon (0 + 0) + (0 + \mu) &= 2 \\[0.8em] \mu &= 2 \end{align*}\]
Parameterwert \(\mu = 2\) in die Geradengleichung der \(x_{3}\)-Achse einsetzen:
\[\overrightarrow{S}_{x_{3}} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + 2 \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 2 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{3}} (0|0|2)\]
Lage der Ebene \(E\) sowie der Geraden \(g\) im Koordinatensystem
Mithilfe der ermittelten Schnittpunkte der Ebene \(E\) mit den Koordinatenachsen (Spurpunkte) und den sich daraus ergebenden Spurgeraden lässt sich die Ebene \(E\) im Koordinatensystem darstellen. Eine Spurgerade verläuft durch die beiden Spurpunkte \(S_{x_{1}}\) und \(S_{x_{2}}\). Da die Ebene \(E\) parallel zur \(x_{2}\)-Achse liegt (siehe oben), verlaufen zwei weitere Spurgeraden jeweils durch einen Spurpunkt und parallel zur \(x_{2}\)-Achse.
Um den Verlauf der Geraden \(g\) veranschaulichen zu können, bestimmt man einen weiteren Punkt auf der Geraden \(g\). Es bietet sich der Schnittpunkt der Geraden \(g\) mit der \(x_{1}x_{3}\)-Ebene oder der \(x_{1}x_{2}\)-Ebene an.
Schnittpunkt \(S_{x_{1}x_{3}}\) der Geraden \(g\) mit der \(x_{1}x_{3}\)-Ebene:
\[x_{1}x_{3}\text{-Ebene}\,\colon x_{2} = 0\]
\[g\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
Koordinaten der Geradengleichung in die Ebenengleichung einsetzen:
\[\begin{align*} g \cap x_{1}x_{3}\text{-Ebene}\,\colon \sqrt{2} + \lambda \cdot \sqrt{2} &= 0 & &| -\sqrt{2} \\[0.8em] \lambda \cdot \sqrt{2} &= -\sqrt{2} & &| : \sqrt{2} \\[0.8em] \lambda &= -1 \end{align*}\]
Parameterwert \(\lambda = -1\) in die Geradengleichung von \(g\) einsetzen:
\[\overrightarrow{S}_{x_{1}x_{3}} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} - 1 \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{1}x_{3}}(1|0|1)\]
Schnittpunkt \(S_{x_{1}x_{2}}\) der Geraden \(g\) mit der \(x_{1}x_{2}\)-Ebene:
\[x_{1}x_{2}\text{-Ebene}\,\colon x_{3} = 0\]
\[g\colon \overrightarrow{X} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
Koordinaten der Geradengleichung in die Ebenengleichung einsetzen:
\[\begin{align*} g \cap x_{1}x_{2}\text{-Ebene}\,\colon 2 + \lambda &= 0 & &| - 2 \\[0.8em] \lambda &= -2 \end{align*}\]
Parameterwert \(\lambda = -2\) in die Geradengleichung von \(g\) einsetzen:
\[\overrightarrow{S}_{x_{1}x_{2}} = \begin{pmatrix} 0 \\ \sqrt{2} \\ 2 \end{pmatrix} - 2 \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} = \begin{pmatrix} 2 \\ -\sqrt{2} \\ 0 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{1}x_{2}}(2|-\sqrt{2}|0)\]
Lage der Ebene \(E\) und Verlauf der Geraden \(g\) im Koordinatensystem
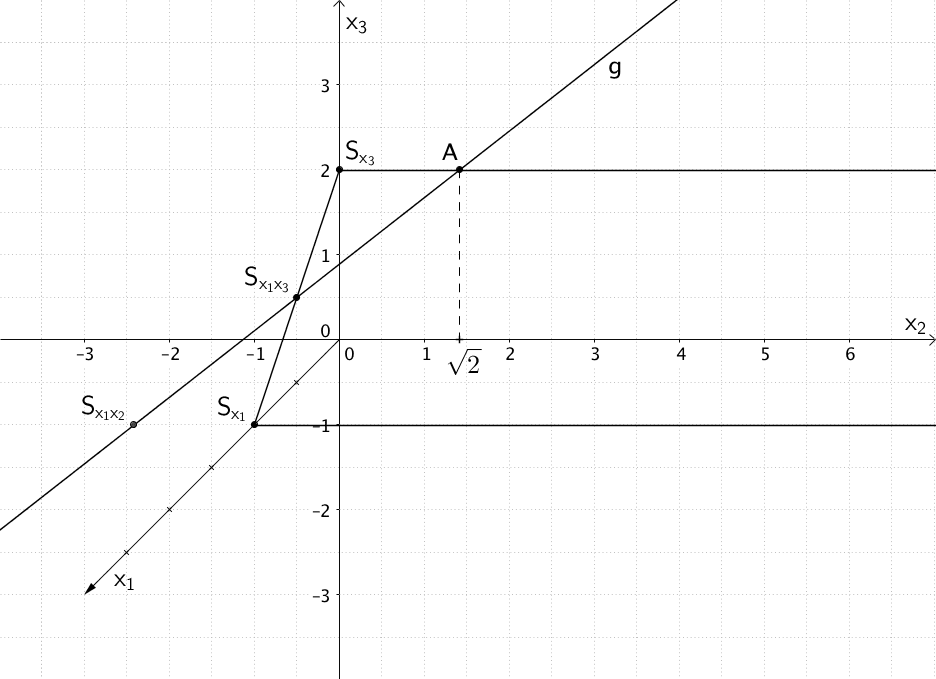
Lage der Ebene \(E\) und Verlauf der Geraden \(g\) im Koordinatensystem (Skizze gemäß Aufgabenstellung)