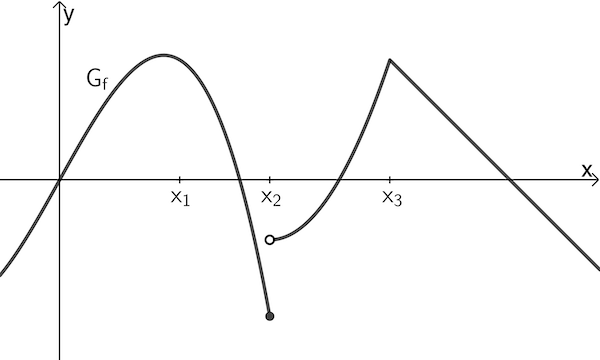
a) Die Abbildung zeigt den Graphen einer Funktion \(f\). Erläutern Sie anhand des Graphen, ob die Funktion \(f\) an den Stellen \(x_1\), \(x_2\) und \(x_3\) jeweils stetig ist.
b) Gegeben ist die Funktion
\[g \colon x \mapsto \begin{cases} \begin{align*} &ax + a &&\text{für} \; x < 1 \\[0.8em] &-2 &&\text{für}\;1 \leq x < 5 \\[0.8em] &b \cdot (x^3 - 10x^2 + 25x)-2 &&\text{für}\;x \geq 5 \end{align*} \end{cases}\enspace\text{mit}\;a, b \in \mathbb R\]
Bestimmen Sie den Wert von \(a\) so, dass \(g\) an der Stelle \(x = 1\) stetig ist und zeigen Sie, dass \(g\) an der Stelle \(x = 5\) unabhängig vom Wert von \(b\) stetig ist.
a) Erläuterung anhand des Graphen, ob \(f\) an den Stellen \(x_1\), \(x_2\) und \(x_3\) stetig ist
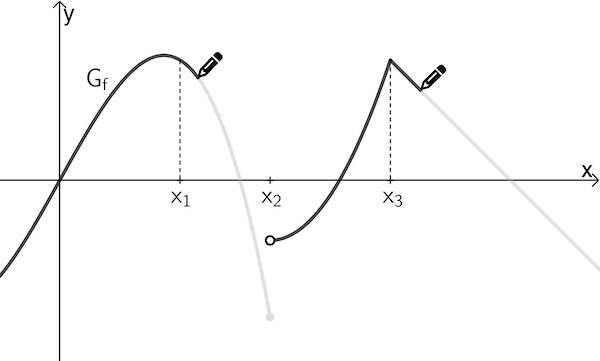
An den Stellen \(x_1\) und \(x_3\) ist die Funktion \(f\) stetig, da ihr Graph dort ohne abzusetzen durchgezeichnet werden kann.
Stetigkeit von Funktionen
Eine Funktion \(f\) ist auf einem Intervall \(I\) stetig, wenn für jede Stelle \(x_0\) des Intervalls gilt, dass der linksseitige und der rechtsseitige Grenzwert an der Stelle \(x_0\) mit dem Funktionswert von \(f\) an der Stelle \(x_0\) übereinstimmen.
\[\lim \limits_{\underset{x\,<\,x_0}{x\,\to\,x_0}}f(x) = \lim \limits_{\underset{x\,>\,x_0}{x\,\to\,x_0}}f(x) = f(x_0)\]
Geometrische Interpretation
Ist eine Funktion \(f\) auf einem Intervall definiert und kann ihr Graph auf diesem Intervall ohne abzusetzen durchgezeichnet werden, so ist \(f\) auf dem Intervall stetig.
An der Sprungstelle \(x_3\) kann der Graph von \(f\) nicht ohne abzusetzen gezeichnet werden. Die Funktion \(f\) ist an der Stelle \(x_3\) unstetig.
b) Bestimmung des Werts von \(a\), Nachweis der Stetigkeit unabhängig von \(b\) an der Stelle \(x = 5\)
Wert von \(\boldsymbol{a}\), sodass \(\boldsymbol{g}\) an der Stelle \(\boldsymbol{x = 1}\) stetig ist
\[g \colon x \mapsto \begin{cases} \begin{align*} &ax + a &&\text{für} \; x < \textcolor{#cc071e}{1} \\[0.8em] &\textcolor{#0087c1}{-2} &&\text{für}\;\textcolor{#cc071e}{1} \leq x < 5 \\[0.8em] &b \cdot (x^3 - 10x^2 + 25x)-2 &&\text{für}\;x \geq 5 \end{align*} \end{cases}\enspace\text{mit}\;a, b \in \mathbb R\]
Stetigkeit von Funktionen
Eine Funktion \(f\) ist auf einem Intervall \(I\) stetig, wenn für jede Stelle \(x_0\) des Intervalls gilt, dass der linksseitige und der rechtsseitige Grenzwert an der Stelle \(x_0\) mit dem Funktionswert von \(f\) an der Stelle \(x_0\) übereinstimmen.
\[\lim \limits_{\underset{x\,<\,x_0}{x\,\to\,x_0}}f(x) = \lim \limits_{\underset{x\,>\,x_0}{x\,\to\,x_0}}f(x) = f(x_0)\]
Geometrische Interpretation
Ist eine Funktion \(f\) auf einem Intervall definiert und kann ihr Graph auf diesem Intervall ohne abzusetzen durchgezeichnet werden, so ist \(f\) auf dem Intervall stetig.
Die Funktion \(g\) ist an der „Nahtstelle" \(\textcolor{#cc071e}{x = 1}\) stetig, wenn die Graphen der Terme \(ax + a\) und \(-2\), welche die Funktion \(g\) links und rechts von der „Nahtstelle" beschreiben, ohne abzusetzen durchgezeichnet werden können (graphische Interpretation der Stetigkeit).
Dafür wird überprüft, für welchen Wert von \(a\) der Term \(ax + a\) an der Stelle \(\textcolor{#cc071e}{x = 1}\) den Wert \(\textcolor{#0087c1}{-2}\) annimmt. So, als wäre der Term \(ax + a\) für \(x = 1\) definiert und dessen Graph würde im Punkt \((\textcolor{#cc071e}{1}|\textcolor{#0087c1}{-2})\) enden.
\[\begin{align*}a \cdot \textcolor{#cc071e}{1} + a &= \textcolor{#0087c1}{-2} \\[0.8em] 2a &= -2 &&| : 2 \\[0.8em] a &= -1\end{align*}\]
Für \(a = -1\) ist die Funktion \(g\) an der Stelle \(x = 1\) stetig.
Anmerkung
Die formal korrekte Überprüfung der Stetigkeit von \(f\) an der Stelle \(x = 1\) erfolgt mithilfe des links- und rechtsseitigen Grenzwerts an der Stelle \(\textcolor{#cc071e}{x = 1}\).
\[\begin{align*}\lim \limits_{\underset{x\,<\,\textcolor{#cc071e}{1}}{x\,\to\,\textcolor{#cc071e}{1}}}f(x) &= \lim \limits_{\underset{x\,>\,\textcolor{#cc071e}{1}}{x\,\to\,\textcolor{#cc071e}{1}}}f(x) = f(\textcolor{#cc071e}{1}) \\[0.8em] \lim \limits_{\underset{x\,<\,\textcolor{#cc071e}{1}}{x\,\to\,\textcolor{#cc071e}{1}}} (\underbrace{ax + a}_{\to\,2a}) &= \lim \limits_{\underset{x\,>\,\textcolor{#cc071e}{1}}{x\,\to\,\textcolor{#cc071e}{1}}} \textcolor{#0087c1}{-2} = \textcolor{#0087c1}{-2} \\[0.8em] 2a &= -2 &&| : 2 \\[0.8em] a &= -1 \end{align*}\]
Für \(a = -1\) ist die Funktion \(g\) an der Stelle \(x = 1\) stetig.
Nachweis, dass \(\boldsymbol{g}\) an der Stelle \(\boldsymbol{x = 5}\) unabhängig vom Wert von \(\boldsymbol{b}\) stetig ist
\[g \colon x \mapsto \begin{cases} \begin{align*} &ax + a &&\text{für} \; x < 1 \\[0.8em] &\textcolor{#0087c1}{-2} &&\text{für}\;1 \leq x < \textcolor{#cc071e}{5} \\[0.8em] &b \cdot (x^3 - 10x^2 + 25x)-2 &&\text{für}\;x \geq \textcolor{#cc071e}{5} \end{align*} \end{cases}\enspace\text{mit}\;a, b \in \mathbb R\]
Es ist zu zeigen, dass der Term \(b \cdot (x^3 - 10x^2 + 25x)-2\), der die Funktion \(g\) rechts von der „Nahtstelle" \(\textcolor{#cc071e}{x = 5}\) beschreibt, unabhängig vom Wert von \(b\) für \(\textcolor{#cc071e}{x = 5}\) den Wert \(\textcolor{#0087c1}{-2}\) annimmt.
\[\begin{align*}b \cdot (\textcolor{#cc071e}{5}^3 - 10 \cdot \textcolor{#cc071e}{5}^2 + 25 \cdot \textcolor{#cc071e}{5})-2 &= \textcolor{#0087c1}{-2} \\[0.8em] b \cdot (125 - 250 + 125) - 2 &= -2 \\[0.8em] b \cdot 0 - 2 &= -2 \\[0.8em] -2 &= -2\end{align*}\]
Also ist die Funktion \(g\) an der Stelle \(x = 5\) unabhängig vom Wert von \(b\) stetig.


